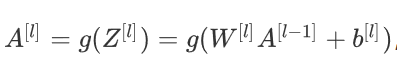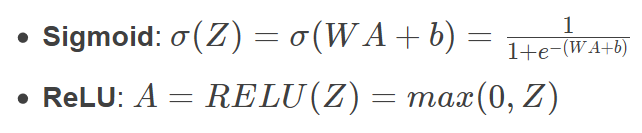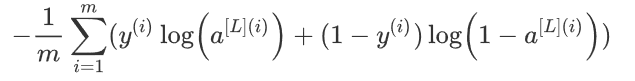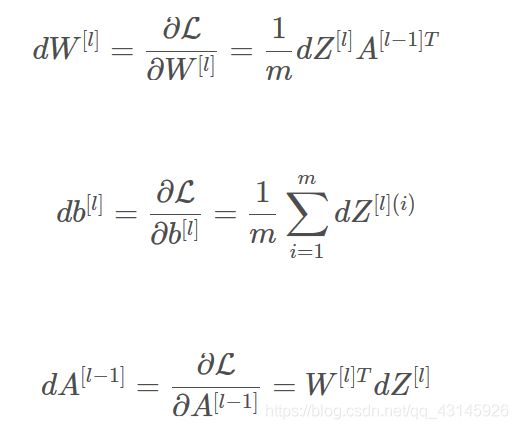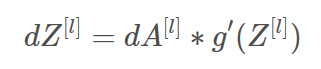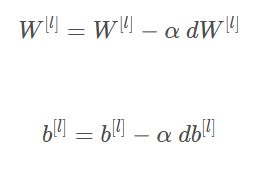深度学习 | 一步步搭建多层神经网络

吴恩达《深度学习》L1W4作业1&2
此篇的任务是：构建用于图像分类的深度神经网络
任务所需要的资料可以在末尾参考链接第一条找到。

我用的环境是天池的notebook

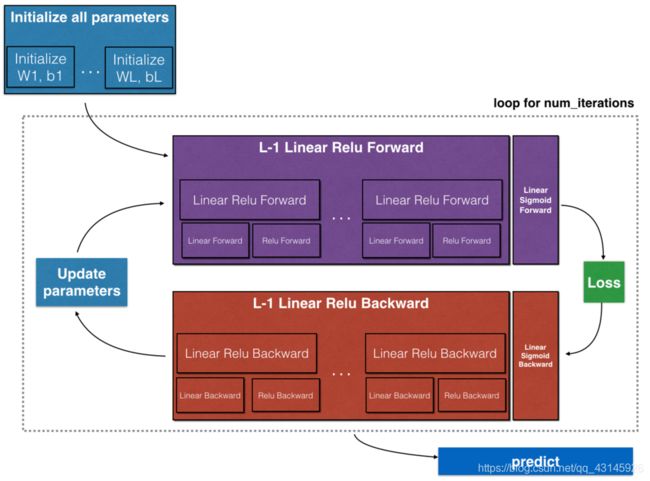
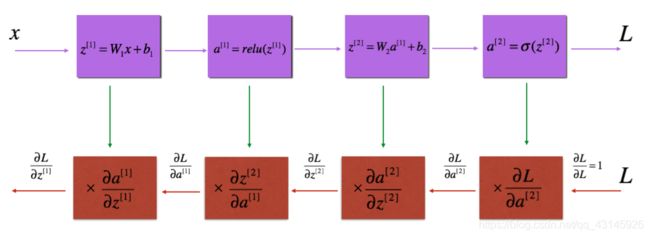
• 构建单层神经网络的前向后向传播的完整过程如下图：

• 构建神经网络的总步骤：
  • 初始化网络参数
  • 前向传播
    • 计算一层中的线性求和部分
    • 计算激活函数的部分
    • 集合线性求和与激活函数
  • 计算误差
  • 反向传播
    • 线性部分的反向传播
    • 激活函数部分的反向传播
    • 结合线性部分与激活函数的反向传播
  • 更新参数
• 注意：对于每个前向函数，都有一个相应的后向函数。所以我们在喜欢发模块中都会在cache中存储一些值，cache的值对计算梯度很有用。

1 初始化

1.1二层神经网络

• 模型结构为：Linear->ReLU->Linear->Sigmoid

• 随机初始化权重矩阵，确保准确的维度，使用np.random.randn(shape)*0.01

• 将偏差初始化为0：使用np.zeros(shape)

• 导入软件包

import numpy as np
import h5py
import matplotlib.pyplot as plt
import testCases
from dnn_utils import sigmoid, sigmoid_backward,relu,relu_backward
import lr_utils

np.random.seed(1)

• 初始化参数并测试

def initialize_parameters(n_x,n_h,n_y):
    W1=np.random.randn(n_h,n_x)*0.01
    b1=np.zeros((n_h,1))
    W2=np.random.randn(n_y,n_h)*0.01
    b2=np.zeros((n_y,1))
    
    assert(W1.shape==(n_h,n_x))
    assert(b1.shape==(n_h,1))
    assert(W2.shape==(n_y,n_h))
    assert(b2.shape==(n_y,1))
    
    parameters={
     
        "W1":W1,
        "b1":b1,
        "W2":W2,
        "b2":b2
    }
    return parameters
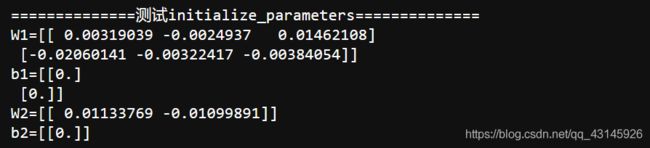
print("==============测试initialize_parameters==============")
parameters=initialize_parameters(3,2,1)
print("W1="+str(parameters["W1"]))
print("b1="+str(parameters["b1"]))
print("W2="+str(parameters["W2"]))
print("b2="+str(parameters["b2"]))

1.2 推广到L层神经网络

• 更深的L层神经网络初始化更复杂，因为存在更多的权重矩阵和偏差向量。在初始化参数时要时刻注意各层之间的维度匹配。
• 以输入X的大小为(12288,209)为例。
  
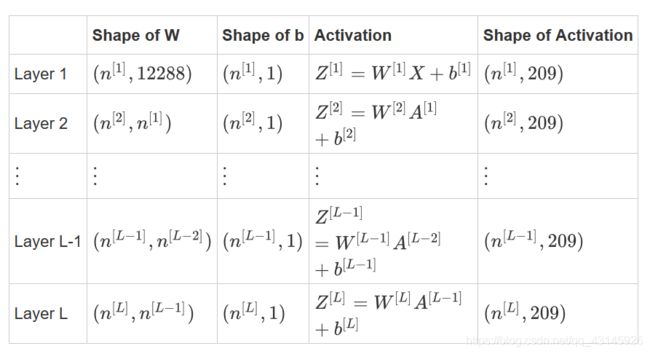
• 在python中计算WX+b时，使用广播，比如：
  
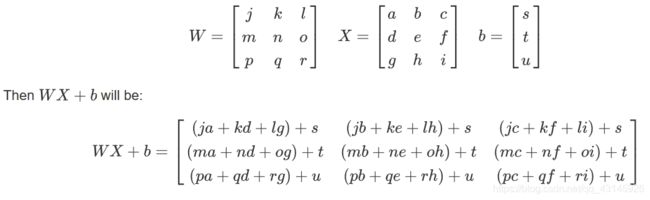
• 任务：实现L层神经网络的初始化
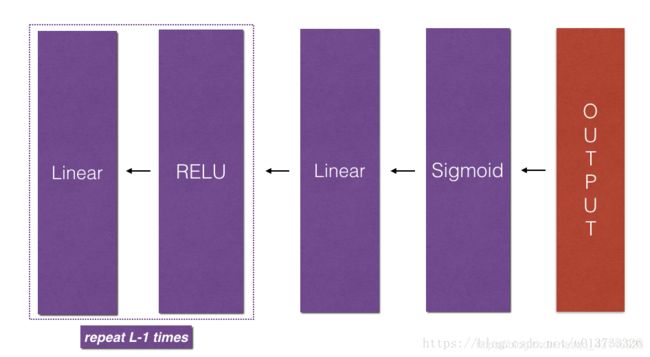
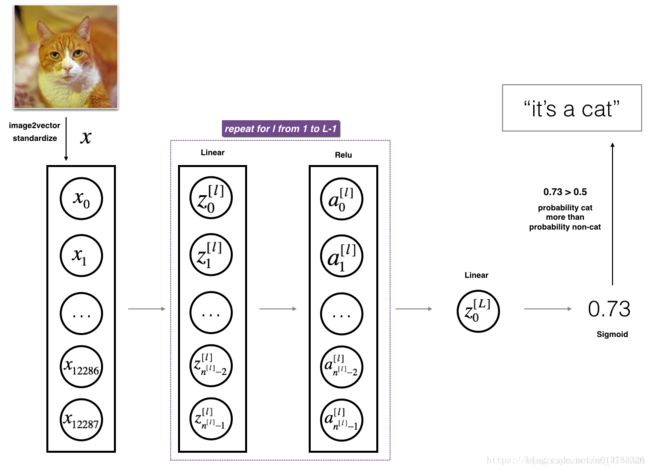
  • 模型的结构为：【Linear->ReLU】*(L-1)->Linear->Sigmoid。也就是说L-1层使用ReLU作为激活函数，最后一层采用sigmoid激活函数输出。
  • 随机初始化权重函数。使用np.random.rand(shape)*0.01
  • 初始化偏差为0。使用np.zeros(shape)
  • 我们将在不同的layer_dims变量中存储n[l]，即不同层中的神经元数。
    • 例如，上次的“二维数据分类模型”的layer_dims为[2,4,1]：即有两个输入，一个隐藏层包含4个隐藏单元，一个输出层包含1个输出单元。
    • 因此，维度：W1=[4,2],b1=[4,1],W2=[1,4],b1=[1,1]
  • 例如L=1(一层神经网络)的实现：

if L==1:
	parameters["W"+str(L)]=np.random.randn(layer_dims[1],layer_dims[0])*0.01
	parameters["b"+str(L)]=np.zeros((layer_dims[1],1))

• 初始化L层神经网络：

def initialize_parameters_deep(layers_dims):
    np.random.seed(3)
    parameters = {
     }
    L = len(layers_dims)
    
    for l in range(1,L):
        parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
        parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
        
        #确保我要的数据的格式是正确的
        assert(parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l-1]))
        assert(parameters["b" + str(l)].shape == (layers_dims[l], 1))
        
    return parameters


#测试initialize_parameters_deep
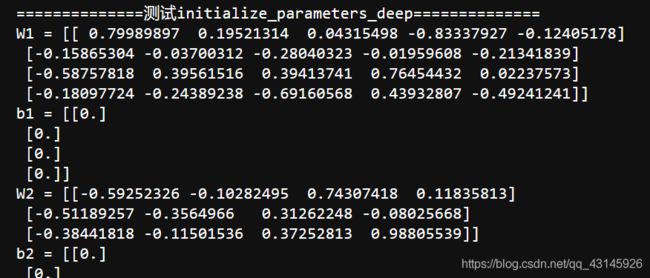
print("==============测试initialize_parameters_deep==============")
layers_dims = [5,4,3]
parameters = initialize_parameters_deep(layers_dims)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

2 前向传播

• 前向传播有三个步骤：
  • Linear
  • Linear->activation,其中激活函数将会使用ReLU或Sigmoid
  • [Linear->ReLU]*(L-1)->Linear->Sigmoid
• 线性正向传播模块（向量化）使用以下公式计算：
  

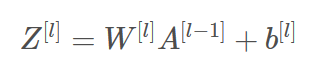
2.1 二层模型前向传播的线性部分【Linear】

def linear_forward(A,W,b):
    """
    实现前向传播的线性部分
    参数：
        A-来自上一层（或输入数据）的激活，维度为（上一层的系欸但数量，示例的数量）
        W-权重矩阵，numpy数组，维度为（当前图层的节点数量，前一图层的节点数量）
        b-偏向量，numpy向量，维度为（当前图层节点数量，1）
        
    返回：
        Z-激活功能的输入，称为预激活函数
        cache-一个包含 A W b 的字典，存储这些变量以有效地计算后向传递
    """
    Z=np.dot(W,A)+b
    assert(Z.shape==(W.shape[0],A.shape[1]))
    cache=(A,W,b)
    
    return Z,cache

#测试linear_forward
print("==============测试linear_forward==============")
A,W,b = testCases.linear_forward_test_case()
Z,linear_cache = linear_forward(A,W,b)
print("Z = " + str(Z))

2.2 二层模型前向传播线性激活部分【Linear->Activation】

• 数学表达式为
  
• 激活函数如下，其中sigmoid作为输出层的激活函数，其他的都用ReLU
  

def linear_activation_forward(A_prev,W,b,activation):
    """
    实现Linear->Activation这一层的前向传播
    
    参数：
        A_prev -来自上一层（输入层）的激活，维度为（上一层的节点数量，示例数）
        W-权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
        b-偏向量，numpy阵列，维度为（当前层的节点数量，1）
        activation-选择在此层中使用的激活函数名，字符串类型，【“sigmoid”| “relu”】
    返回：
        A-激活函数的输出，也称为激活后发值
        cache-一个包含 linear_cache和activation_cache的字典，我们需要存储它以有效地计算后向传播
    """
    if activation=="sigmoid":
        Z,linear_cache=linear_forward(A_prev,W,b)
        A,activation_cache=sigmoid(Z)
    elif activation=="relu":
        Z,linear_cache=linear_forward(A_prev,W,b)
        A,activation_cache=relu(Z)
        
    assert(A.shape==(W.shape[0],A_prev.shape[1]))
    cache=(linear_cache,activation_cache)
    
    return A,cache

#测试linear_activation_forward
print("==============测试linear_activation_forward==============")
A_prev, W,b = testCases.linear_activation_forward_test_case()

A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("sigmoid，A = " + str(A))

A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("ReLU，A = " + str(A))

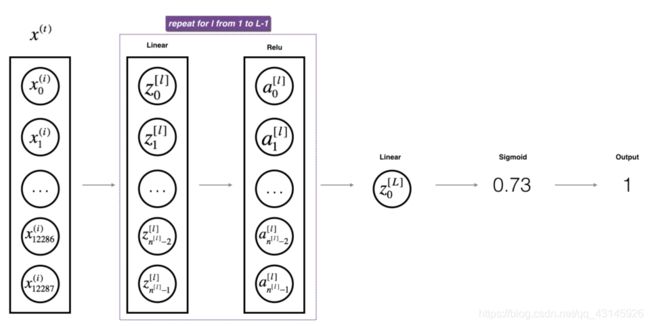
2.3 推广到L层神经网络

• 为了实现L层神经网络，我们需要一个函数来复制（带有ReLU的linear_activation_forward）L-1次，然后再用一个（带有Sigmoid的linear_activation_forward）跟踪它。
  
• 在下面代码中AL表示以下公式，也可以叫做Yhat
  
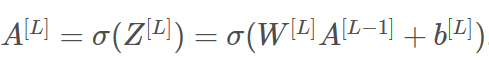
• 多层模型的前向传播计算模型代码：

def L_model_forward(X,parameters):
    """
    实现[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID计算前向传播，也就是多层网络的前向传播，为后面每一层都执行LINEAR和ACTIVATION
    
    参数：
        X - 数据，numpy数组，维度为（输入节点数量，示例数）
        parameters - initialize_parameters_deep（）的输出
    
    返回：
        AL - 最后的激活值
        caches - 包含以下内容的缓存列表：
                 linear_relu_forward（）的每个cache（有L-1个，索引为从0到L-2）
                 linear_sigmoid_forward（）的cache（只有一个，索引为L-1）
    """
    caches=[]
    A=X
    L=len(parameters)//2
    for l in range(1,L):
        A_prev=A
        A,cache=linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],"relu")
        caches.append(cache)
        
    AL,cache=linear_activation_forward(A,parameters['W'+str(L)],parameters['b'+str(L)],"sigmoid")
    caches.append(cache)
    
    assert(AL.shape==(1,X.shape[1]))
    
    return AL,caches

#测试L_model_forward
print("==============测试L_model_forward==============")
X,parameters = testCases.L_model_forward_test_case()
AL,caches = L_model_forward(X,parameters)
print("AL = " + str(AL))
print("caches 的长度为 = " + str(len(caches)))

3 损失函数

• 交叉熵损失J：
  

def compute_cost(AL,Y):
    """

    参数：
        AL - 与标签预测相对应的概率向量，维度为（1，示例数量）
        Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（1，数量）

    返回：
        cost - 交叉熵成本
    """
    m=Y.shape[1]
    cost=-np.sum(np.multiply(np.log(AL),Y)+np.multiply(np.log(1-AL),1-Y))
    
    cost=np.squeeze(cost)
    assert(cost.shape==())
    
    return cost
    
#测试compute_cost
print("==============测试compute_cost==============")
Y,AL = testCases.compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))

4 反向传播

• 反向传播用于计算相对于参数的损失函数的梯度，流程如下：

• 构建反向传播的步骤：
  • Linear后向计算
  • Linear->Activation 后向计算，其中Activation计算ReLU或者Sigmoid的结果
  • [Linear->ReLU]*(L-1)->Linear-Sigmoid后向计算整个模型

4.1 二层模型线性部分

def linear_backward(dZ,cache):
    """
    为单层实现反向传播的线性部分（第L层）

    参数：
         dZ - 相对于（当前第l层的）线性输出的成本梯度
         cache - 来自当前层前向传播的值的元组（A_prev，W，b）

    返回：
         dA_prev - 相对于激活（前一层l-1）的成本梯度，与A_prev维度相同
         dW - 相对于W（当前层l）的成本梯度，与W的维度相同
         db - 相对于b（当前层l）的成本梯度，与b维度相同
    """
    A_prev,W,b=cache
    m=A_prev.shape[1]
    dW=np.dot(dZ,A_prev.T)/m
    db=np.sum(dZ,axis=1,keepdims=True)/m
    dA_prev=np.dot(W.T,dZ)
    
    assert(dA_prev.shape==A_prev.shape)
    assert(dW.shape==W.shape)
    assert(db.shape==b.shape)
    
    return dA_prev,dW,db
    
#测试linear_backward
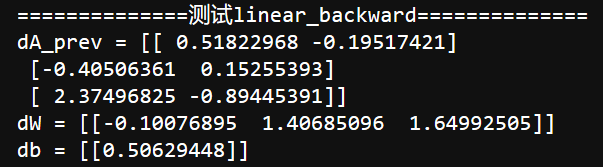
print("==============测试linear_backward==============")
dZ, linear_cache = testCases.linear_backward_test_case()

dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))

4.2 二层模型线性激活部分

• 为了帮助你实现linear_activation_backward，作业资料中提供了两个函数：
• sigmoid_backward:实现了sigmoid()函数的反向传播：

dZ=sigmoid_backward(dA,activation_cache)

• relu_backward:实现了relu（）函数的反向传播：

dZ=relu_backward(dA,activation_cache)

• 如果g是激活函数，那么sigmoid_backward和relu_backward这样计算：
  

def linear_activation_backward(dA,cache,activation="relu"):
    """
    实现Linear ->Activation层的后向传播
        dA - 当前层L激活后的梯度值
        cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache,activation_cache)
        activation - 要在此层中使用的激活函数名，字符串类型，【“sigmoid" | "relu"】
    返回：
        dA_prev-相对于激活（前一层L-1）的成本梯度值，与A_prev维度相同
        dW-相对于W（当前层L）的成本梯度值，与W的维度相同
        db-当对于b（当前层L）的成本梯度值，与b的维度相同
    """
    linear_cache, activation_cache = cache
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        
    return dA_prev,dW,db

#测试linear_activation_backward
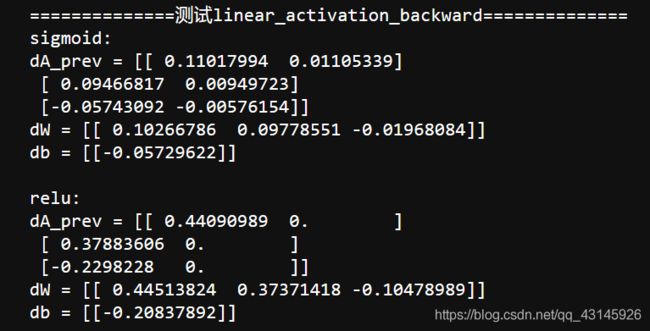
print("==============测试linear_activation_backward==============")
AL, linear_activation_cache = testCases.linear_activation_backward_test_case()
 
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")
 
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))

4.3 推广到L层模型

• 计算AL的偏导，可以使用：

dAL=-(np.divide(Y,AL)-np.divide(1-Y,1-AL))

• 构建多层模型向后传播函数事，可以使用上面激活后的梯度dAL继续向后计算。

def L_model_backward(AL,Y,caches):
    """
    对[LINEAR->RELU]*(L-1)->LINEAR->SIGMOID组执行反向传播，也就是多层网络的向后传播
    参数：
    AL-概率向量，正向传播的输出 （L_model_forward()）
    Y-标签向量（不是猫为0，是猫为1）维度为（1，数量）
    caches-包含以下内容的cache列表：
        linear_cativation_forward("relu")的cache，不包含输出层
        linear_activation_forward("sigmoid")的cache
    
    返回：
    grads-具有梯度值的字典
        grads["dA"+str(l)]=...
        grads["dW"+str(l)]=...
        grads["db"+str(l)]=...
    """
    grads={
     }
    L=len(caches)
    m=AL.shape[1]
    Y=Y.reshape(AL.shape)
    dAL=-(np.divide(Y,AL)-np.divide(1-Y,1-AL))
    
    current_cache=caches[L-1]
    grads["dA"+str(L)],grads["dW"+str(L)],grads["db"+str(L)]=linear_activation_backward(dAL,current_cache,"sigmoid")
    
    for l in reversed(range(L-1)):
        current_cache=caches[l]
        dA_prev_temp,dW_temp,db_temp=linear_activation_backward(grads["dA"+str(l+2)],current_cache,"relu")
        grads["dA"+str(l+1)]=dA_prev_temp
        grads["dW"+str(l+1)]=dW_temp
        grads["db"+str(l+1)]=db_temp
        
        return grads
    
    #测试L_model_backward
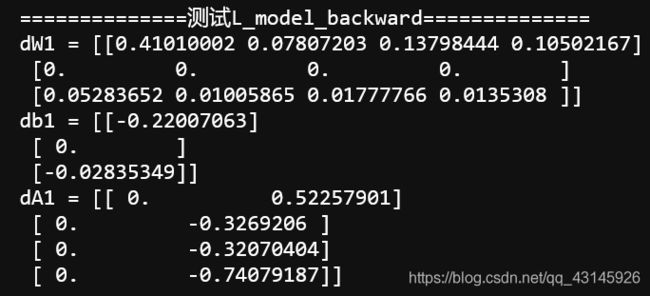
print("==============测试L_model_backward==============")
AL, Y_assess, caches = testCases.L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))

4.4 更新参数

• 更新参数的公式如下，α是学习率。
  

def update_parameters(parameters,grads,learning_rate):
    """
    使用梯度下降更新参数
    
    参数：
    parameters -包含你的参数字典
    grads- 包含梯度值的字典，是L——model——backward的输出
    
    返回：
    parameters - 包含更新参数的字典
        参数["W"+str(l)]=...
        参数["b"+str(l)]=...
    """
    L=len(parameters)//2
    for l in range(L):
        parameters["W"+str(l+1)]=parameters["W"+str(l+1)]-learning_rate*grads["dW"+str(l+1)]
        parameters["b"+str(l+1)]=parameters["b"+str(l+1)]-learning_rate*grads["db"+str(l+1)]
        
    return parameters
    
    
#测试update_parameters
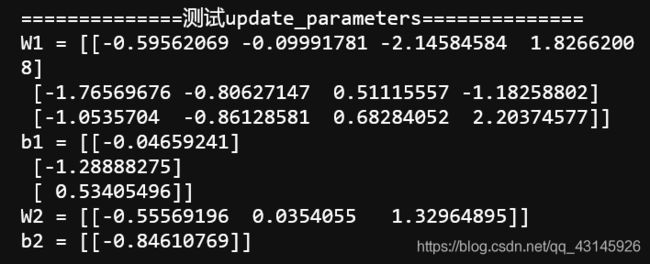
print("==============测试update_parameters==============")
parameters, grads = testCases.update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)
 
print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))

• 至此，实现神经网络的所需函数我们都完成了，下面可以开始搭建神经网络了

---

5 搭建两层神经网络

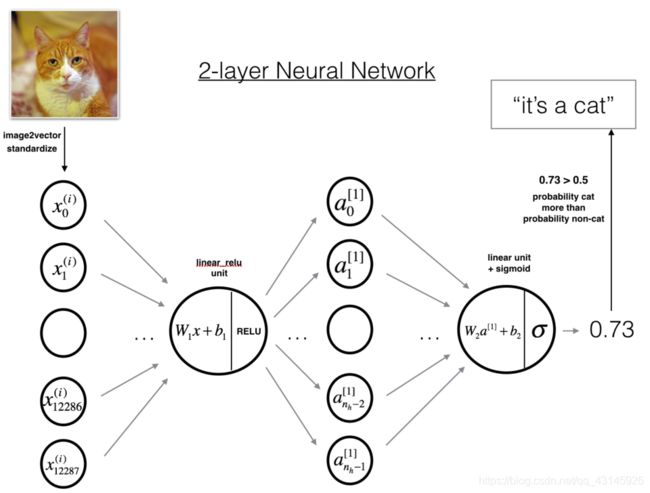
• 两层的神经网络模型图：

• 该模型可以概括为：Input->Linear->Relu->Linear->Sigmoid->Output

def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False,isPlot=True):
    """
    实现一个两层的神经网络，【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
    参数：
        X - 输入的数据，维度为(n_x，例子数)
        Y - 标签，向量，0为非猫，1为猫，维度为(1,数量)
        layers_dims - 层数的向量，维度为(n_y,n_h,n_y)
        learning_rate - 学习率
        num_iterations - 迭代的次数
        print_cost - 是否打印成本值，每100次打印一次
        isPlot - 是否绘制出误差值的图谱
    返回:
        parameters - 一个包含W1，b1，W2，b2的字典变量
    """
    np.random.seed(1)
    grads = {
     }
    costs = []
    (n_x,n_h,n_y) = layers_dims
    
    """
    初始化参数
    """
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    """
    开始进行迭代
    """
    for i in range(0,num_iterations):
        #前向传播
        A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
        A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
        
        #计算成本
        cost = compute_cost(A2,Y)
        
        #后向传播
        ##初始化后向传播
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        ##向后传播，输入：“dA2，cache2，cache1”。 输出：“dA1，dW2，db2;还有dA0（未使用），dW1，db1”。
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
        
        ##向后传播完成后的数据保存到grads
        grads["dW1"] = dW1
        grads["db1"] = db1
        grads["dW2"] = dW2
        grads["db2"] = db2
        
        #更新参数
        parameters = update_parameters(parameters,grads,learning_rate)
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        #打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            #记录成本
            costs.append(cost)
            #是否打印成本值
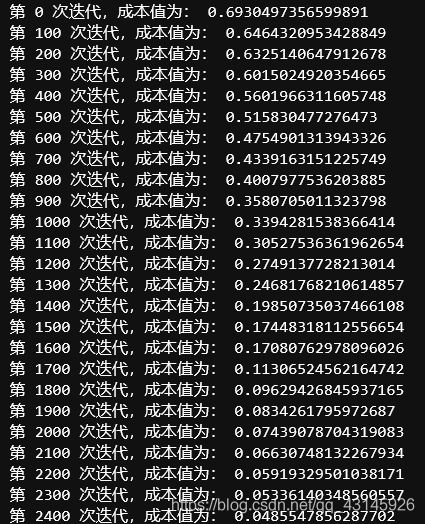
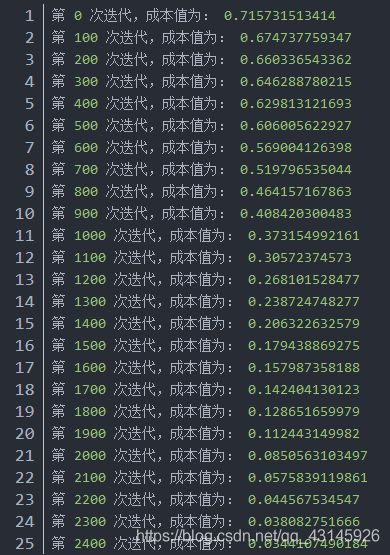
            if print_cost:
                print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
    #迭代完成，根据条件绘制图
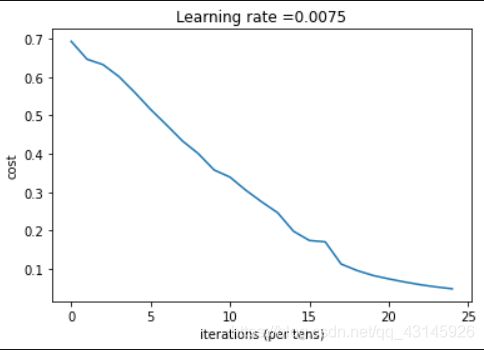
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    
    #返回parameters
    return parameters

• 加载图片数据集，可以参照之前第二周的作业

train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()

train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T 
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y

• 开始正式训练

n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x,n_h,n_y)

parameters = two_layer_model(train_x, train_set_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True,isPlot=True)

• 迭代完成后开始预测

def predict(X, y, parameters):
    """
    该函数用于预测L层神经网络的结果，当然也包含两层
    
    参数：
     X - 测试集
     y - 标签
     parameters - 训练模型的参数
    
    返回：
     p - 给定数据集X的预测
    """
    
    m = X.shape[1]
    n = len(parameters) // 2 # 神经网络的层数
    p = np.zeros((1,m))
    
    #根据参数前向传播
    probas, caches = L_model_forward(X, parameters)
    
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
    
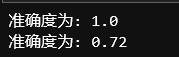
    print("准确度为: "  + str(float(np.sum((p == y))/m)))
        
    return p

predictions_train = predict(train_x, train_y, parameters) #训练集
predictions_test = predict(test_x, test_y, parameters) #测试集

• 在之前深度学习 | 用1层隐藏层的神经网络分类二维数据用的是单层是隐藏层训练出来是70%，现在用了二层的提升到72%

---

6 搭建多层神经网络

def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False,isPlot=True):
    """
    实现一个L层神经网络：[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID。
    
    参数：
	    X - 输入的数据，维度为(n_x，例子数)
        Y - 标签，向量，0为非猫，1为猫，维度为(1,数量)
        layers_dims - 层数的向量，维度为(n_y,n_h,···,n_h,n_y)
        learning_rate - 学习率
        num_iterations - 迭代的次数
        print_cost - 是否打印成本值，每100次打印一次
        isPlot - 是否绘制出误差值的图谱
    
    返回：
     parameters - 模型学习的参数。 然后他们可以用来预测。
    """
    np.random.seed(1)
    costs = []
    
    parameters = initialize_parameters_deep(layers_dims)
    
    for i in range(0,num_iterations):
        AL , caches = L_model_forward(X,parameters)
        
        cost = compute_cost(AL,Y)
        
        grads = L_model_backward(AL,Y,caches)
        
        parameters = update_parameters(parameters,grads,learning_rate)
        
        #打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            #记录成本
            costs.append(cost)
            #是否打印成本值
            if print_cost:
                print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
    #迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    return parameters

• 加载数据集

train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()

train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T 
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y

• 正式训练

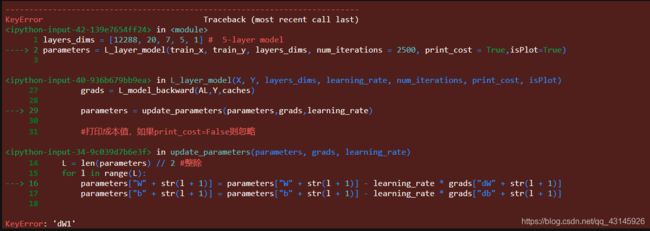
layers_dims = [12288, 20, 7, 5, 1] #  5-layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True)

• 运行正常应该是这样的，（我截的参考里的图）
  

• 但是我的报错如下，我还没找到解决的方法，先挂会儿，之后回来修改
  

7 分析准确率

• 可以查看哪些东西被错误的标记了：

def print_mislabeled_images(classes, X, y, p):
    """
	绘制预测和实际不同的图像。
	    X - 数据集
	    y - 实际的标签
	    p - 预测
    """
    a = p + y
    mislabeled_indices = np.asarray(np.where(a == 1))
    plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
    num_images = len(mislabeled_indices[0])
    for i in range(num_images):
        index = mislabeled_indices[1][i]
        
        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
        plt.axis('off')
        plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8"))


print_mislabeled_images(classes, test_x, test_y, pred_test)

• 分析可以得知原因，模型表现欠佳的几种类型图像包括：
  • 猫身体在一个不同的位置
  • 猫出现在相似颜色的背景下
  • 不同的猫的颜色和品种
  • 相机角度
  • 图片的亮度
  • 比例变化（猫的图像非常大或很小）

---

参考资料：

• 【中文】【吴恩达课后编程作业】Course 1 - 神经网络和深度学习 - 第四周作业(1&2)
• 吴恩达《深度学习》L1W4作业1
• 吴恩达《深度学习》L1W4作业2