基于改进人工蜂群算法的无线传感器网络覆盖优化策略
文章目录
- 一、理论基础
-
- 1、人工蜂群算法
- 2、改进人工蜂群算法
- 二、仿真与分析
-
- 1、参数设置
- 2、MATLAB程序实现
- 三、算法对比
- 四、参考文献
一、理论基础
1、人工蜂群算法
请参考这里。
2、改进人工蜂群算法
请参考文献[1]。
二、仿真与分析
1、参数设置
IABC(改进人工蜂群算法)实验部分参数设置如下:部署区域为50×50,网格点设置为0.4×0.4,种群规模40,迭代次数为400,传感器感知半径 r s = 5 rs=5 rs=5。ABC的实验参数设置同IABC一样。
2、MATLAB程序实现
- 计算WSN覆盖率函数
function z = computeCover(x, y, L, R, data)
%% 适应度函数:WSN的覆盖率
% input:
% x 圆心横坐标
% y 圆心纵坐标
% L 区域边长
% R 通信半径
% data 离散粒度
% output:
% z 覆盖率
N = length(x); % 节点总个数
[m, n] = meshgrid(1:data:L); % 离散化区域内的点
[row, col] = size(m);
for i = 1:N
D = sqrt((m-x(i)).^2+(n-y(i)).^2); % 计算坐标点到圆心的距离
[m0, n0] = find(D <= R); % 检测出圆覆盖点的坐标
Ind = (m0-1).*col+n0; % 坐标与索引转化
M(Ind) = 1; % 改变覆盖状态
end
scale = sum(M(1:end))/(row*col); % 计算覆盖比例
z = scale;
- ABC算法轮盘赌选择蜜源位置的函数
function i = RouletteWheelSelection(P)
r = rand;
C = cumsum(P);
i = find(r <= C, 1, 'first');
end
- 主函数
%% 清空环境变量
clc;
clear;
close all;
%% 问题设定
L = 50; % 区域边长
n = 35; % 节点个数
rs = 5; % 感知半径
data = 0.4; % 离散粒度
CostFunction = @(x, y, L, R, data) computeCover(x, y, L, R, data);% 目标函数(覆盖率)
%% ABC参数
MaxIt = 400; % 最大迭代次数
nPop = 40; % 蜂群大小
nOnlooker = nPop; % 侦察蜂个数
limit = 100; % 探索极值限制参数
a = 1; % 加速度系数上限
VarSize = [n, 2];
%% 初始化
% 置空蜜蜂矩阵
empty_bee.Position = [];
empty_bee.Cost = [];
% 初始化蜂群数组
pop = repmat(empty_bee, nPop, 1);
% 初始化最优解
BestSol.Cost = 0;
% 产生初始种群
for i = 1:nPop
pop(i).Position = unifrnd(0, L, VarSize);
pop(i).Cost = CostFunction(pop(i).Position(:, 1), pop(i).Position(:, 2), L, rs, data);
if pop(i).Cost > BestSol.Cost
BestSol = pop(i);
end
end
% 丢解计数器
C = zeros(nPop, 1);
% 保存最优函数值的数组
BestCost = zeros(MaxIt, 1);
save data1;
%% 初始结果显示
gbest = BestSol.Position;
disp('初始位置:' );
disp([num2str(gbest)]);
disp(['初始覆盖率:', num2str(BestSol.Cost)]);
% 初始覆盖图
figure;
for i = 1:n
axis([0 L 0 L]); % 限制坐标范围
x = gbest(:, 1);
y = gbest(:, 2);
sita = 0:pi/100:2*pi; % 角度[0, 2*pi]
hold on;
p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'y');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
'WSN节点', '覆盖区域'});
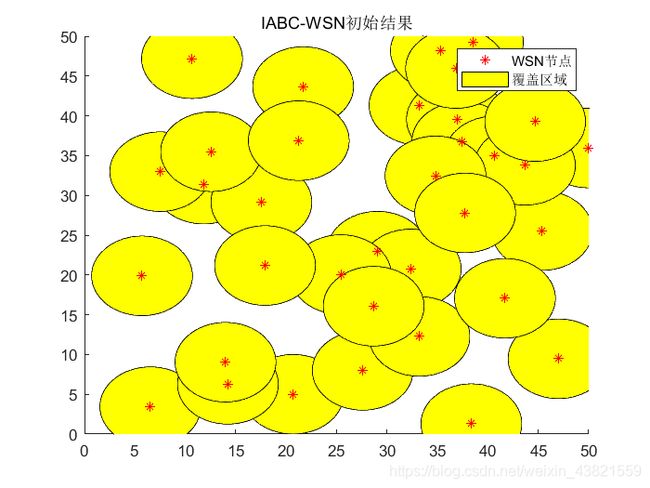
title 'IABC-WSN初始结果';
%% IABC迭代
for it = 1:MaxIt
% 引领蜂
for i = 1:nPop
% 随机选择不等于i的k
K = [1:i-1 i+1:nPop];
k = K(randi([1 numel(K)]));
% 定义加速度系数
phi = a*unifrnd(-1, +1, VarSize);
% 新的蜜蜂位置
newbee.Position = pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
% 边界处理
newbee.Position = max(newbee.Position, 0);
newbee.Position = min(newbee.Position, L);
% 新的蜜蜂函数值
newbee.Cost = CostFunction(newbee.Position(:, 1), newbee.Position(:, 2), L, rs, data);
% 比较
if newbee.Cost >= pop(i).Cost
pop(i) = newbee;
else
C(i) = C(i)+1;
end
end
% 计算适应度值和选择概率
fit = zeros(nPop, 1); % 适应度值
O = zeros(nPop, 1); % 信息素
for i = 1:nPop
% 将函数值转换为适应度
fit(i) = 1/(1+pop(i).Cost);
end
fitmin = min(fit);
fitmax = max(fit);
if fitmin ~= fitmax
O = (fit-fitmin)/(fitmax-fitmin);
end
F = fit; % 适应度函数
Total_Fik = 0;
% 跟随蜂
for i = 1:nOnlooker
% 定义加速度系数
phi = a*unifrnd(-1, +1, VarSize);
if rand <= O(i) % 灵敏度小于信息素
% 计算相互引力系数
for j = 1:nOnlooker
if j ~= i
Total_Fik = Total_Fik+F(j)/(norm(pop(j).Position-pop(i).Position)^2);
end
end
old_pop = pop(i);
for k = 1:nOnlooker
if k ~= i
Fik = norm(F(k)/(norm(pop(k).Position-pop(i).Position)^3) ...
.*(pop(k).Position-pop(i).Position));
% 新的蜜蜂位置
pop(i).Position = pop(i).Position+Fik/Total_Fik.*(pop(i).Position-pop(k).Position);
end
end
newbee.Position = pop(i).Position;
% 边界处理
newbee.Position = max(newbee.Position, 0);
newbee.Position = min(newbee.Position, L);
% 新的蜜蜂函数值
newbee.Cost = CostFunction(newbee.Position(:, 1), newbee.Position(:, 2), L, rs, data);
% 比较
if newbee.Cost >= pop(i).Cost
pop(i) = newbee;
else
pop(i) = old_pop;
C(i) = C(i) + 1;
end
end
end
% 侦察蜂
for i = 1:nPop
if C(i) >= limit % 超出探索极值参数
maxPos = max(pop(i).Position);
minPos = min(pop(i).Position);
for j = 1:n
pop(i).Position(j, :) = minPos+rand(1, 2).*(maxPos-minPos);
end
pop(i).Cost = CostFunction(pop(i).Position(:, 1), pop(i).Position(:, 2), L, rs, data);
C(i) = 0;
end
end
% 最差蜜源的替换
[worst_cost, worst_index] = min([pop.Cost]);
for j = 1:n
% 保存原位置
init_pos = pop(worst_index).Position(j, :);
% 最差蜜源位置更新
pop(worst_index).Position(j, :) = 0+L-rand(1, 2).*pop(worst_index).Position(j, :);
% 边界处理
pop(worst_index).Position(j, :) = min(pop(worst_index).Position(j, :), L);
pop(worst_index).Position(j, :) = max(pop(worst_index).Position(j, :), 0);
% 蜜源更新
pop(worst_index).Cost = CostFunction(pop(worst_index).Position(:, 1), pop(worst_index).Position(:, 2), L, rs, data);
% 比较
if worst_cost < pop(worst_index).Cost
worst_cost = pop(worst_index).Cost;
else
pop(worst_index).Position(j, :) = init_pos;
pop(worst_index).Cost = CostFunction(pop(worst_index).Position(:, 1), pop(worst_index).Position(:, 2), L, rs, data);
end
end
% 更新每轮最优解
for i = 1:nPop
if pop(i).Cost >= BestSol.Cost
BestSol = pop(i);
end
end
% 保存每轮最优解
BestCost(it) = BestSol.Cost;
% 显示迭代信息
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
end
%% 结果显示
BestCost_IABC = BestCost;
gbest = BestSol.Position;
disp('最终位置:' );
disp([num2str(gbest)]);
disp(['最终覆盖率:', num2str(BestSol.Cost)]);
% 最终覆盖图
figure;
for i = 1:n
axis([0 L 0 L]); % 限制坐标范围
x = gbest(:, 1);
y = gbest(:, 2);
sita = 0:pi/100:2*pi; % 角度[0, 2*pi]
hold on;
p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'g');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
'WSN节点', '覆盖区域'});
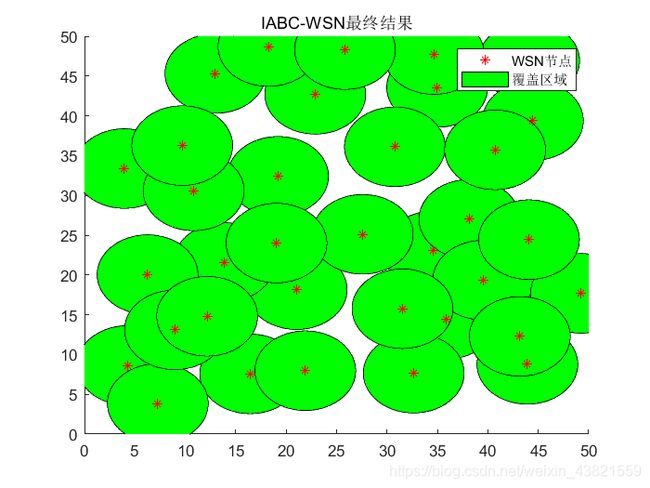
title 'IABC-WSN最终结果';
figure;
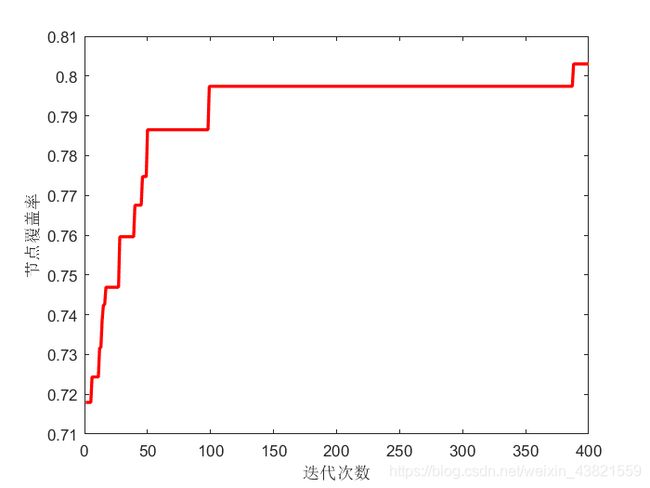
plot(BestCost_IABC, 'r', 'linewidth', 2);
xlabel '迭代次数'; ylabel '节点覆盖率';
load data1.mat;
%%%%%%%%%%%%%%%%%%ABC%%%%%%%%%%%%%%%%%%%%%%
%% 初始化
% 置空蜜蜂矩阵
empty_bee.Position = [];
empty_bee.Cost = [];
% 初始化蜂群数组
pop = repmat(empty_bee, nPop, 1);
% 初始化最优解
BestSol.Cost = 0;
% 产生初始种群
for i = 1:nPop
pop(i).Position = unifrnd(0, L, VarSize);
pop(i).Cost = CostFunction(pop(i).Position(:, 1), pop(i).Position(:, 2), L, rs, data);
if pop(i).Cost > BestSol.Cost
BestSol = pop(i);
end
end
% 丢解计数器
C = zeros(nPop, 1);
% 保存最优函数值的数组
BestCost = zeros(MaxIt, 1);
%% 初始结果显示
gbest = BestSol.Position;
disp('初始位置:' );
disp([num2str(gbest)]);
disp(['初始覆盖率:', num2str(BestSol.Cost)]);
% 初始覆盖图
figure;
for i = 1:n
axis([0 L 0 L]); % 限制坐标范围
x = gbest(:, 1);
y = gbest(:, 2);
sita = 0:pi/100:2*pi; % 角度[0, 2*pi]
hold on;
p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'y');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
'WSN节点', '覆盖区域'});
title 'ABC-WSN初始结果';
%% ABC迭代
for it = 1:MaxIt
% 引领蜂
for i = 1:nPop
% 随机选择不等于i的k
K = [1:i-1 i+1:nPop];
k = K(randi([1 numel(K)]));
% 定义加速度系数
phi = a*unifrnd(-1, +1, VarSize);
% 新的蜜蜂位置
newbee.Position = pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
% 边界处理
newbee.Position = max(newbee.Position, 0);
newbee.Position = min(newbee.Position, L);
% 新的蜜蜂函数值
newbee.Cost = CostFunction(newbee.Position(:, 1), newbee.Position(:, 2), L, rs, data);
% 比较
if newbee.Cost >= pop(i).Cost
pop(i) = newbee;
else
C(i) = C(i)+1;
end
end
% 计算适应度值和选择概率
F = zeros(nPop, 1);
MeanCost = mean([pop.Cost]);
for i = 1:nPop
% 将函数值转换为适应度
F(i) = 1/(1+pop(i).Cost);
end
P = F/sum(F);
% 跟随蜂
for m = 1:nOnlooker
% 选择食物源
i = RouletteWheelSelection(P);
% 随机选择不等于i的k
K = [1:i-1 i+1:nPop];
k = K(randi([1 numel(K)]));
% 定义加速度系数
phi = a*unifrnd(-1, +1, VarSize);
% 新的蜜蜂位置
newbee.Position = pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
% 边界处理
newbee.Position = max(newbee.Position, 0);
newbee.Position = min(newbee.Position, L);
% 新的蜜蜂函数值
newbee.Cost = CostFunction(newbee.Position(:, 1), newbee.Position(:, 2), L, rs, data);
% 比较
if newbee.Cost > pop(i).Cost
pop(i) = newbee;
else
C(i) = C(i) + 1;
end
end
% 侦察蜂
for i = 1:nPop
if C(i) >= limit % 超出探索极值参数
maxPos = max(pop(i).Position);
minPos = min(pop(i).Position);
for j = 1:n
pop(i).Position(j, :) = minPos+rand(1, 2).*(maxPos-minPos);
end
pop(i).Cost = CostFunction(pop(i).Position(:, 1), pop(i).Position(:, 2), L, rs, data);
C(i) = 0;
end
end
% 更新每轮最优解
for i = 1:nPop
if pop(i).Cost >= BestSol.Cost
BestSol = pop(i);
end
end
% 保存每轮最优解
BestCost(it) = BestSol.Cost;
% 显示迭代信息
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
end
%% 结果显示
BestCost_ABC = BestCost;
gbest = BestSol.Position;
disp('最终位置:' );
disp([num2str(gbest)]);
disp(['最终覆盖率:', num2str(BestSol.Cost)]);
% 最终覆盖图
figure;
for i = 1:n
axis([0 L 0 L]); % 限制坐标范围
x = gbest(:, 1);
y = gbest(:, 2);
sita = 0:pi/100:2*pi; % 角度[0, 2*pi]
hold on;
p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'g');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
'WSN节点', '覆盖区域'});
title 'ABC-WSN最终结果';
figure;
plot(BestCost_ABC, 'r', 'linewidth', 2);
xlabel '迭代次数'; ylabel '节点覆盖率';
%% 对比
figure;
t = 1:MaxIt;
plot(t, BestCost_IABC(t), 'r', t, BestCost_ABC(t), 'g', 'linewidth', 2);
legend('IABC', 'ABC');
xlabel '迭代次数'; ylabel '节点覆盖率';
title 'IABC与ABC算法进化过程对比';
- 结果分析
IABC初始随机值和最终的最优解如下:
初始位置:
29.0535 22.9876
6.5267 3.4456
11.8281 31.4067
33.2288 41.3105
38.5128 49.2769
36.9345 39.5577
37.4677 36.7744
20.6875 5.00336
49.9798 35.9529
7.51246 32.9828
27.5914 8.00761
40.692 34.9571
17.5425 29.1371
45.3679 25.5715
21.6789 43.6843
35.3462 48.1567
14.2188 6.25471
43.6795 33.7814
44.6931 39.282
34.8069 32.4572
10.6642 47.1722
12.5533 35.4864
32.3521 20.7616
13.9816 9.03444
33.212 12.2724
36.8439 45.9449
25.4154 20.0453
47.0096 9.46642
5.70646 19.8899
21.2505 36.8794
28.6743 16.0705
38.3655 1.31499
17.8997 21.1879
37.7422 27.7974
41.6989 17.0656
初始覆盖率:0.71796
最终位置:
21.0326 18.1481
43.9177 8.76497
35.9064 14.4497
34.9748 43.5639
30.7755 36.1065
44.0917 46.9257
13.8532 21.5677
6.25125 20.0404
16.4335 7.56279
32.648 7.65552
4.2429 8.62622
34.6046 23.0226
12.9824 45.3154
7.26834 3.84877
38.1753 27.0085
34.6546 47.7028
19.1916 32.3989
21.896 7.97042
3.94899 33.3717
8.96826 13.1053
27.5753 25.1102
22.8835 42.7079
19.0371 24.0061
44.4663 39.3849
39.5472 19.3561
49.2307 17.6891
31.5267 15.7473
12.162 14.8086
18.2448 48.699
10.8258 30.5694
25.8296 48.3197
44.081 24.4425
9.69112 36.2601
40.7159 35.7174
43.1687 12.2773
最终覆盖率:0.80303
三、算法对比
由此可见,经典ABC算法极易陷入局部最优解,原因在于:由于采用轮盘赌选择方式使算法易陷入局部最优,并且跟随蜂邻域搜索过程中没考虑所有引领蜂对它的影响。另外,在迭代过程中,收敛速度会被降低,这是由每一代结束后产生的最坏解导致的。
四、参考文献
[1] 宋苏鸣. 基于改进人工蜂群算法的无线传感器网络覆盖优化策略[D]. 西安电子科技大学, 2014.
[2] Karaboga D . An idea based on honey bee swarm for numerical optimization[J]. 2005.
[3] ~心升明月~. 基于人工蜂群算法的函数寻优算法. CSDN博客.