FPGA 折叠 近似计算实现卷积
@FPGA卷积实现 折叠、moore、近似加法
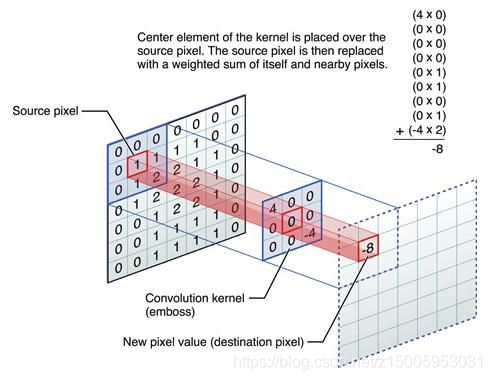
FPGA卷积原理
卷积的原理就不多说了。具体随便百度下都是。这里说下整体的思路就是串行输入,并行计算,原理就是把图像缓存三行,然后抽出每行最右边 的三个乘以卷积核的系数,然后累加这九个结果就可以了,数据矩阵按照数据流形式传进去, 一个一个像素的传进折叠的三层 buf,输出的矩阵也是按照列传出来,进入乘法模块,9 个 乘法相乘的后的数据进入加法树,加法树的底层调用是调用近似加法的模块,并且输出的结 果有效的时候,res-valid 会拉高,由于是计算 valid 型的卷积,这里写的是没有边沿补零 的,所以进入图像矩阵是 3232 型,每次滑动窗口会计算一次卷积的值,并且用状态机控制 数据的读取以及转换,最终得出的矩阵是 3030 型
#实现框图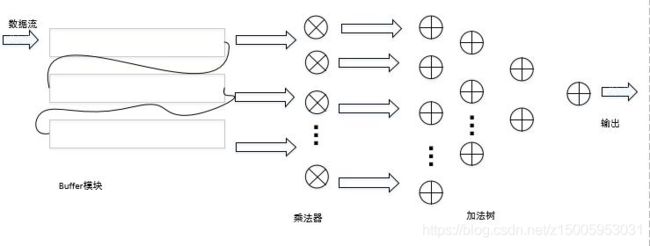
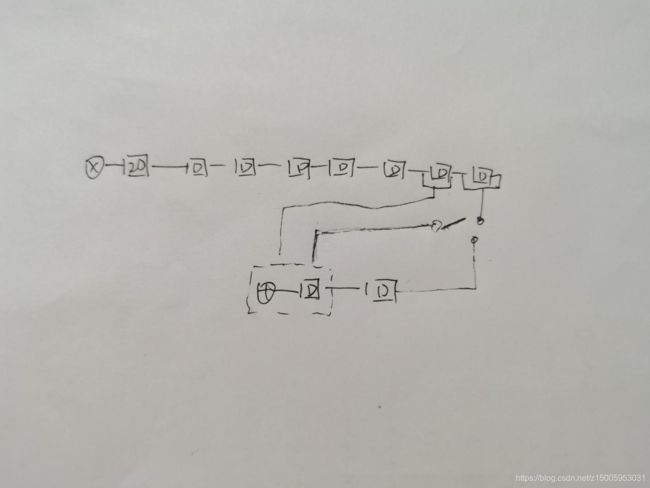
折叠实现手段和思路
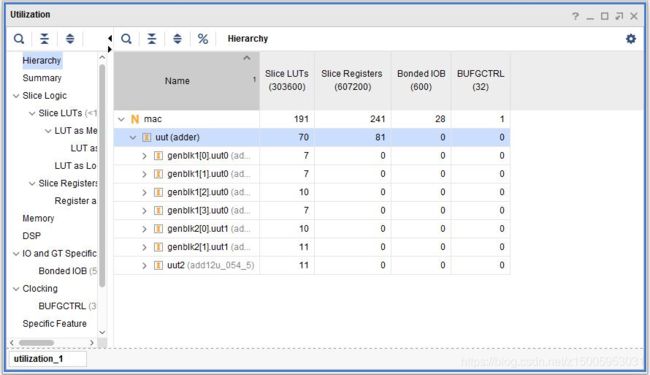
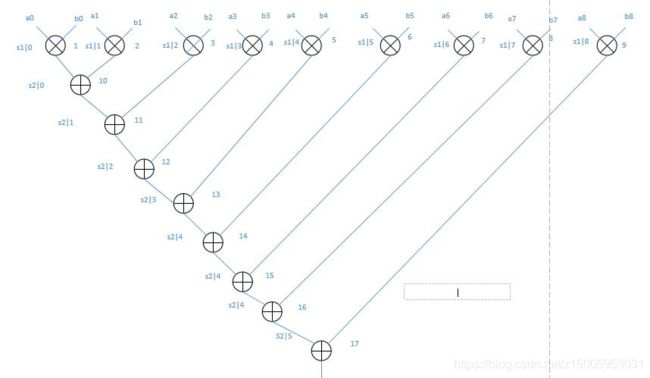
把多个相同运算操作 通过时分复用在单个功能单元(如加法器和乘法器)上执行,达到 资源共享 ,从而减少功能单元数目,从而减少硅片面积。根据以下设计电路图,乘法器 9 个 Pm = 2, 加法 器 8 个 ,Pa = 1,16 条 边, 4 个 寄存 器, 根 据折 叠变 化公 式 : DF(U->V)=N[l+w(e)]+v-(Nl+u+Pu ) 即 DF(U->V)=Nw(e)-Pu+v-u,计算每个节点的 延时,整体计算如下图,举例 D(1—>10)=9-2+0+0=7,说明乘法器 0 的结果,需要延时 7 个 clk 将数据到加法器中进行处理,其余使用类似的思路。
折叠集 Multiplication S1 = {1, 2, 3, 4,5,6,7,8,9} Additions S2 = {10,11,12,13,14,15,16,17} D(1->10)=9(1)-2+0-1=6,D(3->11)=9(1)-2+1-2=6,D(10->11)=9(0)-1+1-0=0 D(4->12)=9(1)-2+2-3=6,D(11->12)=9(0)-1+2-1=0,D(5->13)=9(1)-2+3-4=6 D(12->13)=9(0)-1+3-2=0,D(6->14)=9(1)-2+4-5=6,D(13->14)=9(0)-1+4-3=0 D(7->15)=9(1)-2+5-6=6,D(14->15)=9(0)-1+5-4=0,D(8->16)=9(1)-2+6-7=6 D(15->16)=9(0)-1+6-5=0,D(9->17)=9(1)-2+7-8=0,D(16->17)=9(0)-1+7-6=0
#时序分析

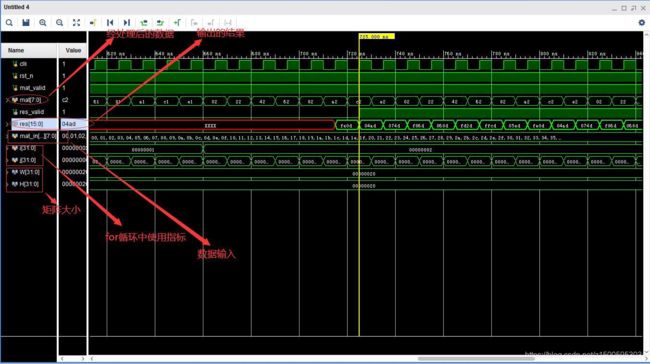
从时钟的角度来看,第一个 clk,计算 a0xb0,第二个 clk,a1xb1,接着总共花费了九 个 clk 将乘法计算完毕,并依次存入后面的寄存器中,然后在第 10 个 clk 的时候,因为乘 法器 0(这里乘法器 1 指( s1 | 0 ),以下相同)的结果延时 9 个 clk 已经到达加法器输入 端,乘法器 2 的结果延时 8 个 clk 到达加法器的输入端,正好计算 a0xb0+a1xb1(这个时候 的加法器的编号应该是( s2 | 0 ));然后在第 10 个 clk 的时候,乘法器 3 的结果经过 8 个 clk 到达加法器,得到的值为:a0xb0+a1xb1+a2xb2(这个加法器编号是( s2 | 1 )); 此后以此类推,需要 17 个时钟计算出 3*3 卷积的值。
实现代码
主要控制部分:
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2021/01/23 16:10:11
// Design Name:
// Module Name: mac
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
module mac #(parameter MAT_W = 32, MAT_H = 32)
(clk,rst_n,mat,mat_valid,res_valid,res);
input clk;
input rst_n;
input signed [7:0] mat;
input mat_valid;
output res_valid;
output signed [15:0] res;//11 15
parameter cnt_start = 2*MAT_W+2;
parameter cal_latency = 5;
parameter cnt_end = MAT_H*MAT_W;
wire signed [7:0] conv0_0 = 0, conv0_1 = 2, conv0_2 = 3;
wire signed [7:0] conv1_0 = 4, conv1_1 = 5, conv1_2 = 6;
wire signed [7:0] conv2_0 = 7, conv2_1 = 8, conv2_2 = 0;
integer i,k;
reg signed [7:0] mat_buf_0[0:1];
reg signed [7:0] mat_buf_1[0:MAT_H-1];
reg signed [7:0] mat_buf_2[0:MAT_H-1];
reg signed [15:0] mult_res [0:8];
reg [4:0] valid_buf;
reg [10:0] ctl_cnt;
wire [16*9-1:0] add_data;//12
wire signed [11:0] add_result;
wire end_flg;
wire signed [15:0] mult_res_buf [0:8];//11
reg [10:0] valid_cnt;
assign end_flg = (ctl_cnt >= cnt_end);
assign res_valid = valid_buf[4] && (valid_cnt < MAT_W-2);
always@(posedge clk or negedge rst_n) begin
if(~rst_n)
valid_cnt <= 11'h0;
else if(valid_buf[4] && (valid_cnt < MAT_W-1))
valid_cnt <= valid_cnt + 1'b1;
else
valid_cnt <= 11'h0;
end
always@(posedge clk or negedge rst_n) begin
if(~rst_n)
ctl_cnt <= 11'h0;
else if(mat_valid && ~end_flg)
ctl_cnt <= ctl_cnt + 1'b1;
else if(end_flg)
ctl_cnt <= 11'h0;
end
always@(posedge clk) begin
if(mat_valid && rst_n) begin
mat_buf_0[0] <= mat;
mat_buf_0[1] <= mat_buf_0[0];
for(k=1; k=cnt_start) && mat_valid;
valid_buf[1] <= valid_buf[0];
valid_buf[2] <= valid_buf[1];
valid_buf[3] <= valid_buf[2];
valid_buf[4] <= valid_buf[3];
end
assign mult_res_buf[0] = mat_buf_2[MAT_W-1] * conv0_0;
assign mult_res_buf[1] = conv0_1 * mat_buf_1[MAT_W-1];
assign mult_res_buf[2] = mat_buf_0[1] * conv0_2;
assign mult_res_buf[3] = mat_buf_2[MAT_W-2] * conv1_0;
assign mult_res_buf[4] = mat_buf_1[MAT_W-2] * conv1_1;
assign mult_res_buf[5] = mat_buf_0[0] * conv1_2;
assign mult_res_buf[6] = mat_buf_2[MAT_W-3] *conv2_0;
assign mult_res_buf[7] = conv2_1*mat_buf_1[MAT_W-3];
assign mult_res_buf[8] = mat * conv2_2;
//multiplier
always@(posedge clk or negedge rst_n) begin
if(~rst_n) begin
for(i=0; i<9; i=i+1)
mult_res[i] <= 12'h0;
end else if(mat_valid) begin
mult_res[0] <= mult_res_buf[0];
mult_res[1] <= mult_res_buf[1];
mult_res[2] <= mult_res_buf[2];
mult_res[3] <= mult_res_buf[3];
mult_res[4] <= mult_res_buf[4];
mult_res[5] <= mult_res_buf[5];
mult_res[6] <= mult_res_buf[6];
mult_res[7] <= mult_res_buf[7];
mult_res[8] <= mult_res_buf[8];
end else begin
for(i=0; i<9; i=i+1)
mult_res[i] <= 12'h0;
end
end
genvar s;
generate
for(s=0; s<9; s=s+1) begin
assign add_data[16*(s+1)-1:16*s] = mult_res[s];//12
end
endgenerate
//add result
adder uut(
.clk(clk),
.data(add_data),
.res(add_result)
);
assign res = add_result;
endmodule
module adder(clk,data, res);
input clk;
input [16*9-1:0] data;//12
output signed [15:0] res;//11
integer i;
reg signed [15:0] f_stage [0:4];//11
reg signed [15:0] s_stage [0:2];//11
reg signed [15:0] t_stage [0:1];//11
reg signed [15:0] fr_stage;
wire signed [15:0] f [0:4];//11
wire signed [15:0] s [0:2];//11
wire signed [15:0] t [0:1];//11
wire signed [15:0] fr;//11
generate
genvar k,j;
for(k=0;k<4;k=k+1) begin
add12u_054 uut0(.O(f[k]), .A(data[(2*k+2)*16-1 -:16]), .B(data[(2*k+1)*16-1 -:16]));//12
end
for(j=0;j<2;j=j+1) begin
add12u_054 uut1(.O(s[j]), .A(f_stage[2*j+1]), .B(f_stage[2*j]));
end
endgenerate
add12u_054 uut2(.O(t[0]), .A(s_stage[0]), .B(s_stage[1]));
add12u_054 uut3(.O(fr), .A(t_stage[0]), .B(t_stage[1]));
always@(posedge clk) begin
for (i=0; i<4; i=i+1) begin
f_stage[i] <= f[i];
end
f_stage[4] <= data[16*9-1:16*8];//12
end
always@(posedge clk) begin
for (i=0; i<2; i=i+1) begin
s_stage[i] <= s[i];
end
s_stage[2] <= f_stage[4];
end
always@(posedge clk) begin
t_stage[0] <= s[0];
t_stage[1] <= s[1];
fr_stage <= fr;
end
assign res = fr_stage;
endmodule
###加法器部分(近似加法)
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2021/01/23 16:11:52
// Design Name:
// Module Name: appra_adder
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
module add12u_054(A, B, O);
input [11:0] A, B;
output [12:0] O;
wire c_1,c_2,c_3,c_4;
wire c_5,c_6,c_7,c_8;
wire c_9,c_10,c_11,c_12;
assign c_1=1’b0;
add1 u1(.a(A[0]),.b(B[0]),.cin(c_1),.cout(c_2),.s(O[0]));
add1 u2(.a(A[1]),.b(B[1]),.cin(c_2),.cout(c_3),.s(O[1]));
add1 u3(.a(A[2]),.b(B[2]),.cin(c_3),.cout(c_4),.s(O[2]));
add1 u4(.a(A[3]),.b(B[3]),.cin(c_4),.cout(c_5),.s(O[3]));
add1 u5(.a(A[4]),.b(B[4]),.cin(c_5),.cout(c_6),.s(O[4]));
add1 u6(.a(A[5]),.b(B[5]),.cin(c_6),.cout(c_7),.s(O[5]));
add1 u7(.a(A[6]),.b(B[6]),.cin(c_7),.cout(c_8),.s(O[6]));
add1 u8(.a(A[7]),.b(B[7]),.cin(c_8),.cout(c_9),.s(O[7]));
add1 u9(.a(A[8]),.b(B[8]),.cin(c_9),.cout(c_10),.s(O[8]));
add1 u10(.a(A[9]),.b(B[9]),.cin(c_10),.cout(c_11),.s(O[9]));
add1 u11(.a(A[10]),.b(B[10]),.cin(c_11),.cout(c_12),.s(O[10]));
add1 u12(.a(A[11]),.b(B[11]),.cin(c_12),.cout(O[12]),.s(O[11]));
endmodule
module add1(a,b,cin,cout,s);
input a,b,cin;
output cout,s;
wire c1;
assign cout=a;
assign c1=a^b;
assign s=c1^cin;
endmodule
#测试文件
timescale 1ns/1nsdefine CLK_T 10
module mac_tb();
parameter W = 32;
parameter H = 32;
reg clk, rst_n, mat_valid;
reg [7:0] mat;
wire res_valid;
wire [15:0] res;
reg [7:0] mat_in [0:W*H-1];
integer signed i;
integer j;
always #(`CLK_T/2) clk = ~clk;
initial begin
for(i=0; i
mat_in[i] <= i;
clk = 0;
rst_n = 0;
mat = 0;
#(2CLK_T); rst_n =1; for(i=0;i
end
end
mat_valid = 0;
#(20*`CLK_T);
$stop;
end
mac #(.MAT_W(W), .MAT_H(H))
mac_uut(
.clk(clk),
.rst_n(rst_n),
.mat(mat),
.mat_valid(mat_valid),
.res_valid(res_valid),
.res(res)
);
endmodule