基于V2X的交叉路口碰撞预警算法
过滤算法
-
根据地图匹配算法,可以得到路口区域内驶向交叉口的车辆,从而过滤掉驶出路口的车辆;
-
以交叉口中心为原点,和该点距离大于 d 0 d_0 d0的滤除, d d d的计算公式如下:
d 0 = v 0 ⋅ t 0 d_0=v_0\cdot t_0 d0=v0⋅t0
式中, v 0 v_0 v0为该路口区域的限制的最高速度;一般情况下,提前 3 s 3 \rm s 3s预警是既满足安全要求又不至于干扰驾驶员驾驶,考虑到可能有超速行驶的车辆,取 t 0 = 5 s t_0=5 {\rm s} t0=5s。
预警算法
假设如下:
- 驾驶员遵守交通规则,在接近路口时,会提前开启转向灯。打左转灯代表将左转,右转灯代表将右转,不打转向灯代表将直行;
- 车基本沿着车道中心线行驶。
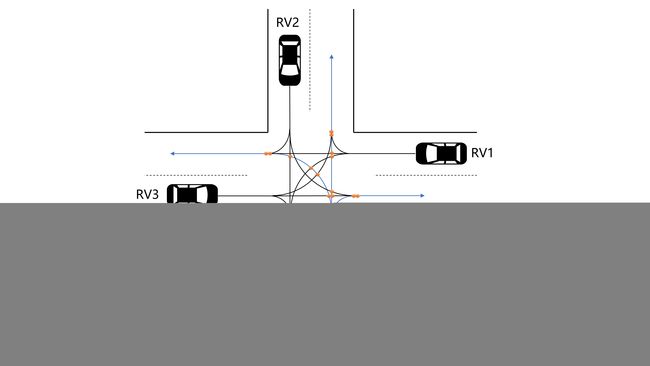
当HV从南边向上驶入交叉口时,同样驶向交叉路口的RV可能来自HV所在位置的左侧、对侧或者右侧,需要分情况讨论不同工况下碰撞点的位置。下述情况中的坐标系均以交叉口中心为原点,正东为 x x x轴,正北为 y y y轴。
HV直行:
从图2可以看出,HV直行时,可能发生碰撞的情况有以下6种(下面列举3种):
一、左侧来车
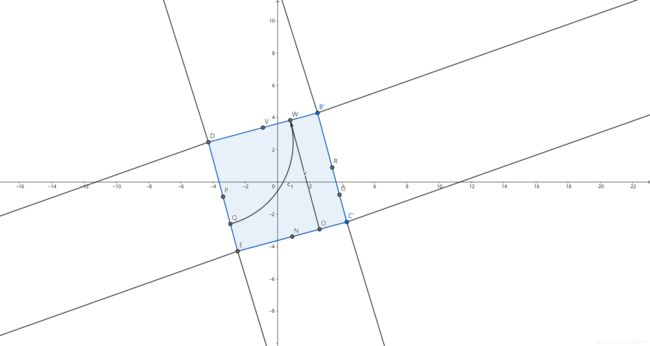
- 直行:此时冲突点如图3所示。
由图可知,冲突点为 Z Z Z点。已知点 O ( x 1 , y 1 ) , Q ( x 2 , y 2 ) O(x_1,y_1),Q(x_2,y_2) O(x1,y1),Q(x2,y2), l O W l_{OW} lOW和 l Q U l_{QU} lQU与 x x x轴的夹角为 θ L 1 , θ L 2 \theta_{L1}, \theta_{L2} θL1,θL2,因此可以得到两条直线的表达式,联立得到以下方程组:
{ y − y 1 = tan ( θ L 1 ) ( x − x 1 ) y − y 2 = tan ( θ L 2 ( x − x 2 ) ) ⟹ [ tan ( θ L 1 ) − 1 tan ( θ L 2 ) − 1 ] [ x y ] = [ tan ( θ L 1 ) ⋅ x 1 − y 1 tan ( θ L 2 ) ⋅ x 2 − y 2 ] \left\{\begin{matrix} y-y_1=\tan(\theta_{L1})(x-x_1) \\ y-y_2=\tan(\theta_{L2}(x-x_2)) \end{matrix}\right. \Longrightarrow \begin{bmatrix} \tan(\theta_{L1}) & -1 \\ \tan(\theta_{L2}) & -1 \end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix} \tan(\theta_{L1})\cdot x_1-y_1 \\ \tan(\theta_{L2})\cdot x_2-y_2\end{bmatrix} { y−y1=tan(θL1)(x−x1)y−y2=tan(θL2(x−x2))⟹[tan(θL1)tan(θL2)−1−1][xy]=[tan(θL1)⋅x1−y1tan(θL2)⋅x2−y2]
解该方程组得冲突点 Z Z Z的坐标为:
{ x c = − y 1 − y 2 − k 1 x 1 + k 2 x 2 k 1 − k 2 y c = k 1 y 2 − k 2 y 1 + k 1 k 2 x 1 − k 1 k 2 x 2 k 1 − k 2 \left\{\begin{array}{l} x_c=-\frac{y_1 -y_2 -k_1 \,x_1 +k_2 \,x_2 }{k_1 -k_2 }\\ y_c=\frac{k_1 \,y_2 -k_2 \,y_1 +k_1 \,k_2 \,x_1 -k_1 \,k_2 \,x_2 }{k_1 -k_2 } \end{array}\right. { xc=−k1−k2y1−y2−k1x1+k2x2yc=k1−k2k1y2−k2y1+k1k2x1−k1k2x2
式中, k 1 = tan ( θ L 1 ) , k 2 = tan ( θ L 2 ) k_1=\tan(\theta_{L1}), k_2={\tan(\theta_{L2})} k1=tan(θL1),k2=tan(θL2).
得到碰撞点后需要判断车是否驶入了路口和是否经过了碰撞点。设HV和 O O O点的连线的角度为 α \alpha α,HV的航向角为 θ H V \theta_{HV} θHV,定义符号函数如下:
s i g n = { 1 ∣ α − θ H V ∣ ≥ π 2 0 ∣ α − θ H V ∣ < π 2 sign = \left\{ \begin{array}{lc} 1 & |\alpha-\theta_{HV}|\geq\frac{\pi}{2} \\ 0 & |\alpha - \theta_{HV}|<\frac{\pi}{2}\end{array} \right. sign={ 10∣α−θHV∣≥2π∣α−θHV∣<2π
s i g n = 1 sign=1 sign=1表示HV已经经过 O O O点, s i g n = 0 sign=0 sign=0表示HV还没有经过 O O O点。同理,也判断HV是否经过 Z Z Z点或者RV是否经过 Q Q Q点和 Z Z Z点。
判断完HV和RV的位置后,需要分段计算HV和RV到碰撞点的距离,设碰撞点坐标为 Z ( x c , y c ) Z(x_c, y_c) Z(xc,yc)。
s H V = { ( x H V − x 1 ) 2 + ( y H V − y 1 ) 2 + ( x 1 − x c ) 2 + ( y 1 − y c ) 2 未 经 过 O 点 ( x H V − x c ) 2 + ( y H V − y c ) 2 经 过 O 点 , 未 经 过 碰 撞 点 s_{HV}=\left\{ \begin{array}{lc} \sqrt{(x_{HV}-x_1)^2+(y_{HV}-y_1)^2}+\sqrt{(x_1-x_c)^2+(y_1-y_c)^2} & 未经过O点 \\ \sqrt{(x_{HV}-x_c)^2+(y_{HV}-y_c)^2} & 经过O点,未经过碰撞点 \end{array}\right. sHV={ (xHV−x1)2+(yHV−y1)2+(x1−xc)2+(y1−yc)2(xHV−xc)2+(yHV−yc)2未经过O点经过O点,未经过碰撞点
s R V = { ( x R V − x 2 ) 2 + ( y R V − y 2 ) 2 + ( x 2 − x c ) 2 + ( y 2 − y c ) 2 未 经 过 Q 点 ( x R V − x c ) 2 + ( y R V − y c ) 2 经 过 Q 点 , 未 经 过 碰 撞 点 s_{RV}=\left\{ \begin{array}{lc} \sqrt{(x_{RV}-x_2)^2+(y_{RV}-y_2)^2}+\sqrt{(x_2-x_c)^2+(y_2-y_c)^2} & 未经过Q点 \\ \sqrt{(x_{RV}-x_c)^2+(y_{RV}-y_c)^2} & 经过Q点,未经过碰撞点 \end{array}\right. sRV={ (xRV−x2)2+(yRV−y2)2+(x2−xc)2+(y2−yc)2(xRV−xc)2+(yRV−yc)2未经过Q点经过Q点,未经过碰撞点
计算TTC:
Δ t = − v + v 2 + 2 a s a \Delta t=\frac{-v+\sqrt{v^2+2as}}{a} Δt=a−v+v2+2as
如果 ∣ Δ t H V − Δ t R V ∣ < t 0 |\Delta t_{HV} - \Delta t_{RV}|
- 左转:此时冲突点如图4所示。
由图可知,冲突点为 W ( x c , y c ) W(x_c,y_c) W(xc,yc)。HV仍未直行, s H V s_{HV} sHV计算公式不变。RV的路径为圆弧, s R V s_{RV} sRV计算公式如下:
s R V = { ( x R V − x 2 ) 2 + ( y R V − y 2 ) 2 + π 2 × ( 1.5 l w ) 未 经 过 Q 点 2 × arcsin ( ( x R V − x c ) 2 + ( y R V − y c ) 2 2 × ( 1.5 l w ) ) ⋅ ( 1.5 l w ) 经 过 Q 点 , 未 经 过 碰 撞 点 s_{RV}=\left\{ \begin{array}{lc} \sqrt{(x_{RV}-x_2)^2+(y_{RV}-y_2)^2}+\frac{\pi}{2}\times(1.5lw) & 未经过Q点 \\ 2\times\arcsin(\frac{\sqrt{(x_{RV}-x_c)^2+(y_{RV}-y_c)^2}}{2\times(1.5lw)})\cdot (1.5lw) & 经过Q点,未经过碰撞点 \end{array}\right. sRV={ (xRV−x2)2+(yRV−y2)2+2π×(1.5lw)2×arcsin(2×(1.5lw)(xRV−xc)2+(yRV−yc)2)⋅(1.5lw)未经过Q点经过Q点,未经过碰撞点
二、对侧来车
- 左转:此时冲突点如图5所示。
由图可知,冲突点为 B 1 B_1 B1点,为了简化计算,可以用 Z Z Z点近似替代 B 1 B_1 B1点。HV仍未直行, s H V s_{HV} sHV计算公式不变。RV的路径为圆弧,设 A 1 A_1 A1的坐标为 A 1 ( x 3 , y 3 ) A_1(x_3,y_3) A1(x3,y3)则, s R V s_{RV} sRV的计算公式如下:
s R V = { ( x R V − x 3 ) 2 + ( y R V − y 3 ) 2 + arccos ( 1 3 ) × ( 1.5 l w ) 未 经 过 A 1 点 2 × arcsin ( ( x R V − x c ) 2 + ( y R V − y c ) 2 2 × ( 1.5 l w ) ) ⋅ ( 1.5 l w ) 经 过 A 1 点 , 未 经 过 碰 撞 点 s_{RV}=\left\{ \begin{array}{lc} \sqrt{(x_{RV}-x_3)^2+(y_{RV}-y_3)^2}+\arccos(\frac{1}{3})\times(1.5lw) & 未经过A_1点 \\ 2 \times \arcsin(\frac{\sqrt{(x_{RV}-x_c)^2+(y_{RV}-y_c)^2}}{2\times(1.5lw)})\cdot (1.5lw) & 经过A_1点,未经过碰撞点 \end{array}\right. sRV={ (xRV−x3)2+(yRV−y3)2+arccos(31)×(1.5lw)2×arcsin(2×(1.5lw)(xRV−xc)2+(yRV−yc)2)⋅(1.5lw)未经过A1点经过A1点,未经过碰撞点
剩余11种情况类似,读者可以参照以上例子自己思考。