LeetCode 33. Search in Rotated Sorted Array(在旋转的排序数组中搜索)

原题

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

题目：
假设按升序排序的数组在事先不知道的某个枢轴处旋转。

如[0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2]).

您被赋予搜索的目标值。如果在数组中找到返回其索引, 否则返回-1。

您可能认为数组中不存在重复项。

算法的运行时复杂性必须是 O (log n) 。

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

My Solution

方案一

class Solution:
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        found = True
        if not nums:
            return -1
      
        for i, count in enumerate(nums):
            if count == target:
                return i 
            else:
                found = False
                
        if not found:
            return -1
        

方案二

class Solution:
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        found = True
        if not nums:
            return -1
      
        for i in range(len(nums)):
            if nums[i] == target:
                return i
            else:
                found = False
        
        if not found:
            return -1  

Reference answer
$logn$ 的复杂度，升序数组，可以联想到二分查找法，但是这里的数组是旋转过的，所以要考虑基于二分查找的思想进行变种。可以用到数学的中方法——分情况讨论。
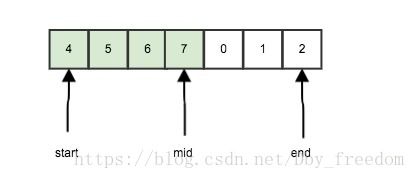
基于二分查找，mid = (start + end) / 2;，mid的情况可以分为两种：

• nums[mid] > nums[start]，这种情况说明顺序断层的点发生在右边，因此左半边是升序的，这时候再判断target的值

  • 如果target在nums[start] 和 nums[mid]之间，因为左半边是升序的，说明target就在左半边的数组中，在[start, mid-1]中递归查找；
  • 如果target < nums[start] 或 target > nums[mid]，说明target在断层的地方或target在左半没有断层继续递增的位置，都说明在右侧，在[mid + 1, end]中递归查找
    

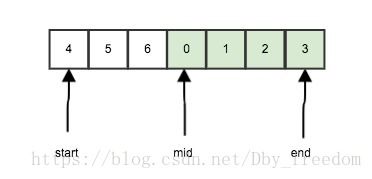
• nums[mid] < nums[end]，说明在左侧已经发生了断层，因此右侧是顺序的：

  • 如果target在nums[mid]和nums[end]之间，因为右半边是升序的，说明target就在右半边的数组中，在[mid + 1, end]中递归查找
  • 同上，相应的，在[start, mid-1]中递归查找
    

class Solution:
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        if not nums:
            return -1
        start = 0
        end = len(nums) - 1
        while start <= end:
            mid = int((start + end)/2)
            if nums[mid] == target:
                return mid
            if nums[mid] >= nums[start]:    # 当nums[mid]属于左边升序序列时
                # if nums[start] <= target < nums[mid]:
                if target>=nums[start] and target<nums[mid]:
                    end = mid - 1
                else:
                    start = mid + 1
            if nums[mid] < nums[end]:    # 当nums[mid]属于右边升序序列时
                # if nums[mid] < target <= nums[end]:
                if target > nums[mid] and target <= nums[end]:
                    start = mid + 1
                else: 
                    end = mid - 1
        return -1

反思：

1. 实践发现，使用for i, count in enumerate(nums) 比使用 for i in range(len(nums)) 效率快很多；前者打败40%左右方法，后者打败80%左右方案；
2. 以后还是尽可能使用 enumerate 代替 range(len(nums))
3. LeetCode的编译排名Python版本不稳定，可能多提交几次就有不同的排名，从算法效率上看二分法针对本题的log n时间复杂度是对应的，且效率比自身用的方法效率高；
4. 要熟悉掌握二分法；