Eigenface(PCA)人脸识别实验

1、ORL数据集简介

ORL人脸数据集一共包含40个不同人的400张图像，是在1992年4月至1994年4月期间由英国剑桥的Olivetti研究实验室创建。

此数据集下包含40个目录，每个目录下有10张图像，每个目录表示一个不同的人。所有的图像是以PGM格式存储，灰度图，图像大小宽度为92，高度为112。对每一个目录下的图像，这些图像是在不同的时间、不同的光照、不同的面部表情（睁眼/闭眼，微笑/不微笑）和面部细节（戴眼镜/不戴眼镜）环境下采集的。所有的图像是在较暗的均匀背景下拍摄的，拍摄的是正脸（有些带有略微的侧偏）。

每个目录分别命名为sx，其中x表示受试者编号（在1到40之间）。在每一个目录所选受试者的10张不同的图像，分别命名为：y.pgm，其中y表示特定对象的不同面部表情、细节（1到10之间）。

ORL人脸数据集下载地址

2、PCA变换原理

在人脸识别过程中，一般把图片看成是向量进行处理，高等数学中我们接触的一般都是二维或三维向量，向量的维数是根据组成向量的变量个数来定的，例如就是一个二维向量，因为其有两个参量。而在将一幅图像抽象为一个向量的过程中，我们把图像的每个像素定为一维，对于一幅的普通图像来说，最后抽象为一个维的高维向量，如此庞大的维数对于后续图像计算式来说相当困难，因此有必要在尽可能不丢失重要信息的前提下降低图像维数，PCA就是降低图像维数的一种方法。图像在经过PCA变换之后，可以保留任意数量的对图像特征贡献较大的维数分量，也就是你可以选择降维到30维或者90维或者其他，当然最后保留的维数越多，图像丢失的信息越少，但计算越复杂。

3、、数据提取与处理

%matplotlib inline
# 导入所需模块
import matplotlib.pyplot as plt
import numpy as np
import os
import cv2

# plt显示灰度图片
def plt_show(img):
    plt.imshow(img,cmap='gray')
    plt.show()

# 读取一个文件夹下的所有图片，输入参数是文件名，返回文件地址列表
def read_directory(directory_name):
    faces_addr = []
    for filename in os.listdir(directory_name):
        faces_addr.append(directory_name + "/" + filename)
    return faces_addr

# 读取所有人脸文件夹,保存图像地址在faces列表中
faces = []
for i in range(1,41):
    faces_addr = read_directory('C:/Users/ASUS/Desktop/att_faces/s'+str(i))
    for addr in faces_addr:
        faces.append(addr)

# 读取图片数据,生成列表标签
images = []
labels = []
for index,face in enumerate(faces):
    # enumerate函数可以同时获得索引和值
    image = cv2.imread(face,0)
    images.append(image)
    labels.append(int(index/10+1))

先读取ORL数据集下的所有图像，同时生成列表标签。下图表示一共有400个标签、400张图像、图像的数据类型以及标签的值。

print(len(labels))
print(len(images))
print(type(images[0]))
print(labels)

# 画出最后20组人脸图像
# 创建画布和子图对象
fig, axes = plt.subplots(10,20
                       ,figsize=(20,10)
                       ,subplot_kw = {
     "xticks":[],"yticks":[]} #不要显示坐标轴
                       )
# 图片x行y列，画布x宽y高
# 填充图像
for i, ax in enumerate(axes.flat):
    ax.imshow(images[i+200],cmap="gray") #选择色彩的模式

以下即位最后20组人脸图像：

4、PCA降维

接下来把每张图片数据降到一维，每张图片的维度是1×10304，与图片的大小92×112=10304相符，将其转换为numpy数组，方便后面的计算。

# 图像数据矩阵转换为一维
image_data = []
for image in images:
    data = image.flatten()
    # a是个矩阵或者数组，a.flatten()就是把a降到一维，默认是按横的方向降
    image_data.append(data)
print(image_data[0].shape)

# 转换为numpy数组
X = np.array(image_data)
y = np.array(labels)
print(type(X))
print(X.shape)

接下来导入sklearn的PCA模块，根据标签，使用train_test_split()划分数据集，训练PCA模型，保留100个维度，输出100个特征脸，可以发现越到后面人脸越模糊，意味着所占的比重越小。

# 导入sklearn的pca模块
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

# 画出每个图像数据降到一维后的矩阵
import pandas as pd
data = pd.DataFrame(X)
data.head()

# 划分数据集
x_train,x_test,y_train,y_test = train_test_split(X, y, test_size=0.2) # train训练，test测试

# 训练PCA模型
pca=PCA(n_components=100) # 保留100个纬度
pca.fit(x_train) # 训练过程

# 返回训练集和测试集降维后的数据集
x_train_pca = pca.transform(x_train) # 转换过程
x_test_pca = pca.transform(x_test)
print(x_train_pca.shape) # 320个训练集，保留了100个特征
print(x_test_pca.shape) # 80个测试集，保留了100个特征

V = pca.components_
V.shape

# 100个特征脸
# 创建画布和子图对象
fig, axes = plt.subplots(10,10
                       ,figsize=(15,15)
                       ,subplot_kw = {
     "xticks":[],"yticks":[]} #不要显示坐标轴
                       )
#填充图像
for i, ax in enumerate(axes.flat):
    ax.imshow(V[i,:].reshape(112,92),cmap="gray") #reshape规定图片的大小，选择色彩的模式

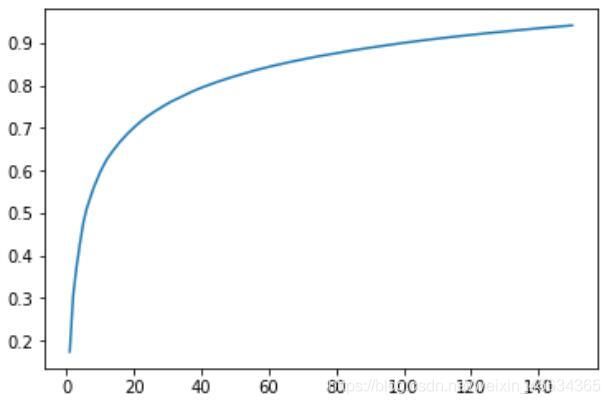
查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比，将其相加，可以得到特征所携带的数据是原始数据的90.056%，从10304维降低到100维，却能够保留90%的信息，这就是PCA降维的魅力所在。

# 该选择多少个特征呢？
# 属性explained_variance_ratio，查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比
# 又叫做可解释方差贡献率
pca.explained_variance_ratio_

# 返回特征所携带的数据是原始数据的多少
pca.explained_variance_ratio_.sum()

画出特征个数和所携带信息数的曲线图。

# 画出特征个数和所携带信息数的曲线图，总共画了150个特征
explained_variance_ratio = []
for i in range(1,151): 
    pca=PCA(n_components=i).fit(x_train)
    explained_variance_ratio.append(pca.explained_variance_ratio_.sum())
plt.plot(range(1,151),explained_variance_ratio)
plt.show()

5、使用OpenCV的EigenFace算法进行识别

原理：将训练集图像和测试集图像都投影到特征向量空间中，再使用聚类方法（最近邻或k近邻等）得到测试集中的每个图像最近的图像，进行分类即可。

cv2.face.EigenFaceRecognizer_create()创建人脸识别的模型，通过图像数组和对应标签数组来训练模型。

predict()函数进行人脸预测，该函数会返回两个元素的数组，第一个是识别个体的标签；第二个是置信度，越小匹配度越高，0表示完全匹配。

getEigenValues() 获得特征值，getEigenVectors() 特征向量，getMean() 均值。

使用OpenCV的EigenFace算法进行识别，首先创建、训练模型，然后挑选一张测试集图片进行预测，此处选择第一张测试集图片，预测的结果是第13个人的图像，与真实结果相符测试集的识别准确率为96%。

# 模型创建与训练
model = cv2.face.EigenFaceRecognizer_create()
model.train(x_train,y_train)

# 预测
res = model.predict(x_test[0])
print(res)

输出：(13, 1653.922120378922)

y_test[0]

输出：13

# 测试数据集的准确率
ress = []
true = 0
for i in range(len(y_test)):
    res = model.predict(x_test[i])
    if y_test[i] == res[0]:
        true = true+1
    else:
        print(i)

print('测试集识别准确率：%.2f'% (true/len(y_test)))

输出：
10
36
53
测试集识别准确率：0.96

6、自定义图片测试

重新构建训练模型，将所有的图片用作训练集，同样保留100个维度，与测试集保持一致，输入自定义的图片，输入的图片是被画过两笔的第一个人的图片。

# 降维
pca=PCA(n_components=100)
pca.fit(X)
X = pca.transform(X)

# 将所有数据都用作训练集
# 模型创建与训练
model = cv2.face.EigenFaceRecognizer_create()
model.train(X,y)

# 输入图片识别，同时进行灰度处理
# 此图片是s1文件夹里的图片画了两笔
img = cv2.imread('C:/Users/ASUS/Desktop/test.jpg',0)
plt_show(img)
print(img.shape)

imgs = []
imgs.append(img)

# 矩阵
image_data = []
for img in imgs:
    data = img.flatten()
    image_data.append(data)
    
test = np.array(image_data)
test.shape

输出：(1, 10304)

# 用训练好的pca模型给图片降维
test = pca.transform(test)
test[0].shape

输出：(100,)

res = model.predict(test)
res
print('人脸识别结果：',res[0])

输出：人脸识别结果： 1

参考博客：opencv基于PCA降维算法的人脸识别（att_faces）

使用Eigenface重构近似的人脸图像

Fisherface(FLD)人脸识别实验

如果你觉得还不错，那就给我点个赞吧(*￣︶￣)