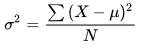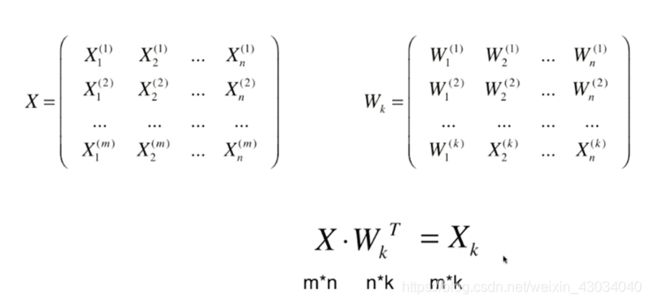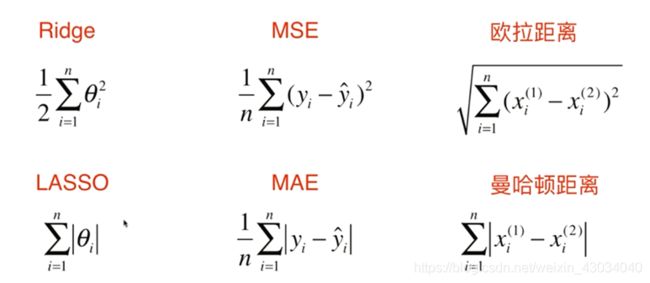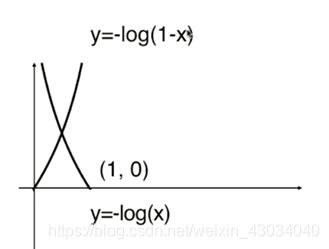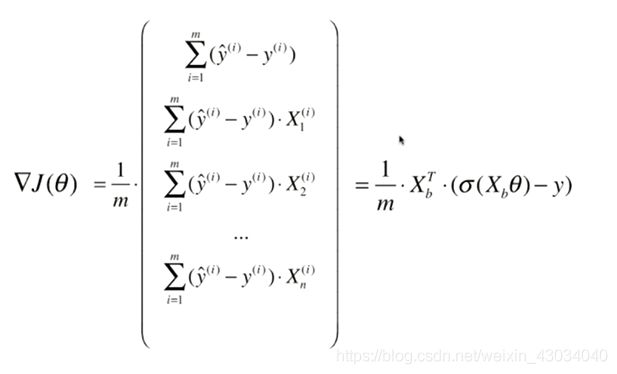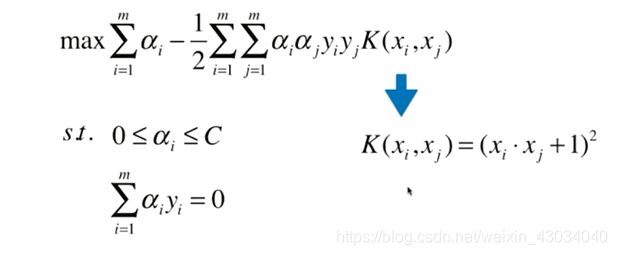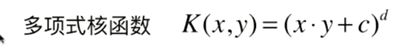机器学习 +python3
文章目录
- 导学
- 机器学习的基础
-
-
- 增强学习
- 批量学习和在线学习
- 参数学习
- 非参数学习
- 哲学思考
-
- 数据重要
- 算法重要
- 简单最好
- 没有免费午餐
- 环境搭建
-
- anaconda
- Jupyter notebook
-
- **%run 加载文件**
- **%timeit**
- **%time**
-
- numpy.array基础
-
- 介绍
- 导入
- 使用
-
- zeros
- ones
- full 自定义大小
- arange
- linspace 等差数列
- 自界randint、seed、random
- 随机正态normal、打乱shuffle、自界uniform
- randrange
- permutation
- 维度 ndim
- 下标访问 X[n][m]
- 切片 X[a:b,n:m]
- reshape
- 合并 concatenate、vstack、hstack
- 分割 split、vsplit、hsplit
- 强制类型转换
- 矩阵运算
-
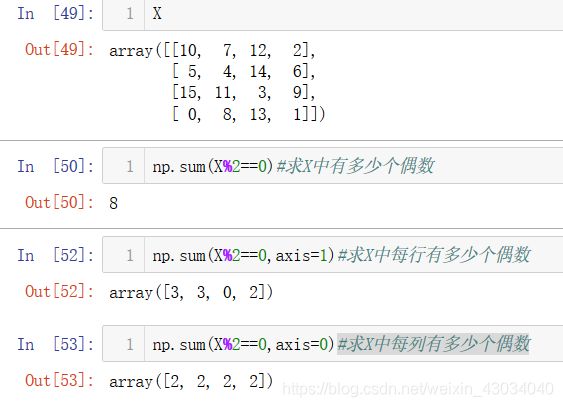
- Universal Function(单矩阵+-*/)
- abs、sin、cos、tan
- exp、power、log、log2、log10
- 矩阵之间运算 +-*/、dot、.T
- 向量与矩阵之间运算 dot
- 向量转矩阵
- 线性代数np.linalg
-
- 逆inv、伪逆pin
- 模norm()
- 聚合运算
-
- sum
-
- **向量**
- 矩阵
- min、max
- 积prod、mean、中位数median、百分位percentile
- 方差var、标准差std
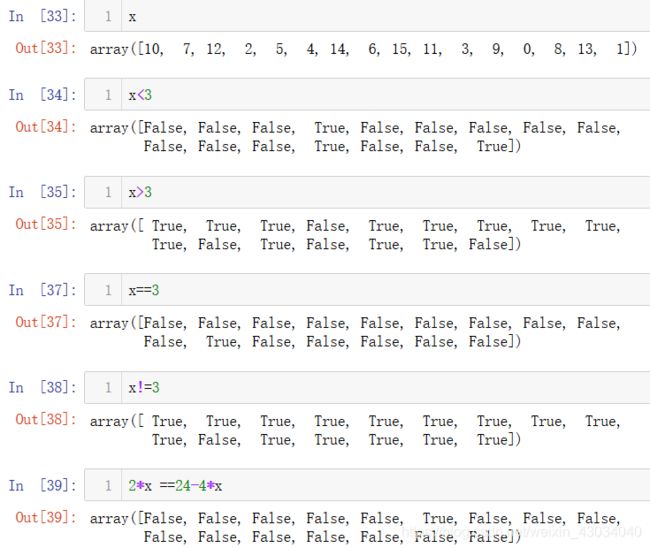
- 比较
-
- > 、== 、!=
- count_nonzero
- any、all、奇偶个数、&、|、非~
- x[x
导学
机器学习的基础
机器学习=监督学习+非监督学习+半监督学习+增强学习
监督学习=分类问题+回归问题
回归任务
- 二分类任务
- 多分类任务
分类任务
结果是一个连续值
回归任务和分类任务是可能可以相互转换的。
例如成绩1–100 转化为 等级
****监督学习:给机器训练的数据拥有“标记”和“答案”
非监督学习:给机器的训练数据没有任何“标记”和“答案”
半监督学习:
增强学习
批量学习和在线学习


批量学习简单,问题是如何适应环境变化,解决方案是定时重新训练。
 优点是能够及时反映新的环境变化,缺点是新的数据带来不好的影响,解决方案是需要加强对数据进行监控。
优点是能够及时反映新的环境变化,缺点是新的数据带来不好的影响,解决方案是需要加强对数据进行监控。
有时数据量太大,无法批量学习,这时可以使用在线学习,一批一批进行学习。
在线学习是对批量学习的改进。不做过多学习
参数学习
非参数学习
不对模型进行过多假设。非参数不是指没有参数
哲学思考
数据重要
算法重要
简单最好
没有免费午餐
环境搭建
anaconda
默认是只有一个root环境,右边是各种包含的包
Jupyter notebook
anaconda 中用到做多的是home的Jupyter notebook。点击launch使用。会进入浏览器。简单方便的创建python3开发环境,进行代码的编写。但只能进行简单编写,大型的还是要用pycharm
快捷键
A : insert cell above
B : insert cell below
Shift-Enter : run cell, select below
Ctrl-Enter : run selected cells
Alt-Enter : run cell and insert below
Y : change cell to code
M : change cell to markdown
魔法命令:
查看所有魔法命令:
%lsmagic
魔法命令帮助说明:
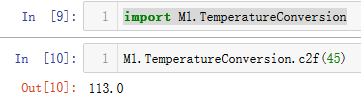
%run? #命令后面加上问好
%run 加载文件
%timeit
%time
![]()
Wall time 是现实世界流失的时间。大概感知使用time,准确使用要timeit.
修改目录:https://www.cnblogs.com/luhuan/p/9054366.html(记得目录使用/)
numpy.array基础
介绍
为何不用python 的数组?
- 运行效率慢。因为数组里面可以存储各种类型的数据,所以处理过程慢
- 无向量和矩阵思想。就算使用python里面的array模块可以限定存储的类型,但依旧只是数组,无法进行矩阵运算。
导入
使用
# 浮点数
nparr2=np.array([1,2,3.4,5.8,9])
nparr2.dtype
#result
dtype('float64')
zeros
#zero
np.zeros(10)
#array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
#默认是float类型
np.zeros(10).dtype
#dtype('float64')
#创建int类型
np.zeros(10,dtype=int)
#array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
#多维数组1
np.zeros((3,5))
#array([[0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0.]])
#多维数组2
np.zeros(shape=(3,5),dtype=int)
#array([[0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0]])
ones
ones和zeros差不多的
np.ones(10)
#array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
np.ones((3,5))
#array([[1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.],
# [1., 1., 1., 1., 1.]])
full 自定义大小
ones是1,zeros是0,那么其他的指定值就需要使用full
np.full(shape=(3,5),fill_value=666.0)
#array([[666., 666., 666., 666., 666.],
# [666., 666., 666., 666., 666.],
# [666., 666., 666., 666., 666.]])
arange
range和arange的比较:
#range
{
i for i in range(0,20,2)}
#{0, 2, 4, 6, 8, 10, 12, 14, 16, 18}
#arange
np.arange(0,20,2)
#array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
true_theta = np.arange(1,12,dtype=float)
linspace 等差数列
#等差数列
np.linspace(0,20,10) #0到20,10个等差数。
#array([ 0. , 2.22222222, 4.44444444, 6.66666667, 8.88888889,
# 11.11111111, 13.33333333, 15.55555556, 17.77777778, 20. ])
自界randint、seed、random
#两个参数
np.random.randint(0,10) #0到10之间的随机数,包含0旦不包含10
#4
#三个参数
np.random.randint(0,10,size=10)#10个 0到10之间的随机数
#array([9, 0, 2, 0, 7, 6, 3, 9, 7, 4])
# 矩阵
np.random.randint(-5,5,size=(2,2))#1 -5到5之间的随机数,矩阵类型 2*2
随机数种子:
#设置随机种子
np.random.seed(666)
np.random.randint(0,10,size=(3,4))
#array([[2, 6, 9, 4],
# [3, 1, 0, 8],
# [7, 5, 2, 5]])
#设置相同的随机种子
np.random.seed(666)
np.random.randint(0,10,size=(3,4))
#array([[2, 6, 9, 4],
# [3, 1, 0, 8],
# [7, 5, 2, 5]])
#随机浮点数
np.random.random()
#0.15551206301509923
X = np.random.random(size=(1000,10))
#1000*10个0到1的浮点数
随机正态normal、打乱shuffle、自界uniform
#均值为0,方差为1的3*5的随机矩阵
np.random.normal(0,1,(3,5))
#array([[ 0.90680574, 0.91860824, 0.40180184, 0.53770265, -0.03535741],
# [ 0.07666546, -0.41779575, 0.96714372, -0.21326813, 0.44076692],
# [ 0.69339587, 0.03820097, -0.18592982, -0.35371521, -1.95332994]])
numpy.random.uniform(low,high,size)
功能:从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
参数介绍:
low: 采样下界,float类型,默认值为0;
high: 采样上界,float类型,默认值为1;
size: 输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出m*n*k个样本,缺省时输出1个值。
randrange
从范围(start,stop,step)返回随机选择的元素
start - 范围的起始点,这将包括在范围内,默认值为0。
stop - 范围的起终点,这将包括在范围内,默认值为1。
step - 跳跃值,不包括在范围内。
randrange(1,100, 2) : 83
randrange(100) : 93
permutation
维度 ndim
import numpy as np
x=np.arange(10)
x
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
X=np.arange(15).reshape(3,5)
X
#array([[ 0, 1, 2, 3, 4],
# [ 5, 6, 7, 8, 9],
# [10, 11, 12, 13, 14]])
x.ndim
#1 #x为一维
X.ndim
#2 #X为二维
x.shape
#(10,) #一维,有十个元素
X.shape
#(3, 5) #二维,3行5列
下标访问 X[n][m]
X[1][1]
#6
X[(1,1)]
#6
X[1,1] #最佳
#6
切片 X[a:b,n:m]
1维切片:
x[0:5]
#array([0, 1, 2, 3, 4])
x[:5]
#array([0, 1, 2, 3, 4])
x[1:]
#array([1, 2, 3, 4, 5, 6, 7, 8, 9])
x[::2]
#array([0, 2, 4, 6, 8])
x[::-1]
#array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
2维切片:
X[:2,:3] #前0到1行,0到2列
#array([[0, 1, 2],
# [5, 6, 7]])
在Python的数组切片中,子切片和原来的数组是没有关系的。
但在numpy中,切片和原数组共用地址空间。一个改动会相互影响。可以使用copy函数来隔离。
subX=X[:2,:3] #截取
subX
#array([[0, 1, 2],
# [5, 6, 7]])
subX[0,0]=100 #修改切片值
X
#array([[100, 1, 2, 3, 4], #原数组也被改变了
# [ 5, 6, 7, 8, 9],
# [ 10, 11, 12, 13, 14]])
subX[0,0]=0
subX=X[:2,:3].copy() #使用copy
subX[0,0]=100
subX
#array([[100, 1, 2],
# [ 5, 6, 7]])
X
#array([[ 0, 1, 2, 3, 4], # subX[0,0]和X[0,0]不同
# [ 5, 6, 7, 8, 9],
# [10, 11, 12, 13, 14]])
reshape
x.reshape不会改变x本身。
x=np.arange(10)
x
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x.reshape(2,5)
#array([[0, 1, 2, 3, 4],
# [5, 6, 7, 8, 9]])
x
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # x本身不会改变
x
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x.shape
#(10,)
x.reshape(10,-1) #将x换成10行,不管一行有几个
#array([[0],
# [1],
# [2],
# [3],
# [4],
# [5],
# [6],
# [7],
# [8],
# [9]])
x.reshape(5,-1) #将x换成5行,不管一行有几个
#array([[0, 1],
# [2, 3],
# [4, 5],
# [6, 7],
# [8, 9]])
合并 concatenate、vstack、hstack
一维向量的合并
x=np.array([1,2,3])
y=np.array([3,2,1])
np.concatenate([x,y]) #合并的参数是列表
#array([1, 2, 3, 3, 2, 1])
二维矩阵的合并
A=np.array([[1,2,3],
[4,5,6]])
np.concatenate([A,A]) #A和自身拼接
#array([[1, 2, 3],
# [4, 5, 6],
# [1, 2, 3],
# [4, 5, 6]])
np.concatenate([A,A],axis=1) #默认axis=0是沿着第一个维度进行拼接,axis=1是沿着第二个维度进行拼接。
#array([[1, 2, 3, 1, 2, 3],
# [4, 5, 6, 4, 5, 6]])
二维矩阵和向量的合并
#方式一:使用reshape
z=np.array([4,5,6]) #z是一维向量
np.concatenate([A,z.reshape(1,-1)]) #使用reshape
#array([[1, 2, 3],
# [4, 5, 6],
# [4, 5, 6]])
#方式二:使用vstack
np.vstack([A,z])
#array([[1, 2, 3],
[4, 5, 6],
[4, 5, 6]])
水平拼接和垂直拼接
A
#array([[1, 2, 3],
# [4, 5, 6]])
B=np.array([[6,8,7],
[8,9,4]])
np.vstack([A,B]) #垂直拼接
#array([[1, 2, 3],
# [4, 5, 6],
# [6, 8, 7],
# [8, 9, 4]])
np.hstack([A,B]) #水平拼接
#array([[1, 2, 3, 6, 8, 7],
# [4, 5, 6, 8, 9, 4]])
分割 split、vsplit、hsplit
一维分割:
x=np.arange(10)
x
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.split(x,[3,7]) #将3,7作为分割点
#[array([0, 1, 2]), array([3, 4, 5, 6]), array([7, 8, 9])]
二维分割:
方法一:
#按行分割
A=np.arange(16).reshape(4,4)
A
#array([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11],
# [12, 13, 14, 15]])
A1,A2=np.split(A,[2]) #默认axis为0,按行分割
A1
#array([[0, 1, 2, 3],
# [4, 5, 6, 7]])
A2
#array([[ 8, 9, 10, 11],
# [12, 13, 14, 15]])
A1,A2=np.split(A,[2],axis=1)#默认axis为1,按列分割
A1
#array([[ 0, 1],
# [ 4, 5],
# [ 8, 9],
# [12, 13]])
A2
#array([[ 2, 3],
# [ 6, 7],
# [10, 11],
# [14, 15]])
方法二:
#1. 按行切
upper,lower=np.vsplit(A,[2])
upper
#array([[0, 1, 2, 3],
# [4, 5, 6, 7]])
lower
#array([[ 8, 9, 10, 11],
# [12, 13, 14, 15]])
#2. 按列切
left ,right = np.hsplit(A,[2])
left
#array([[ 0, 1],
# [ 4, 5],
# [ 8, 9],
# [12, 13]])
right
#array([[ 2, 3],
# [ 6, 7],
# [10, 11],
应用:
data=np.arange(16).reshape(4,4) #原始样本数据
data
#array([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11],
# [12, 13, 14, 15]])
X,y=np.hsplit(data,[-1]) #分离特征和结果
X
#array([[ 0, 1, 2],
# [ 4, 5, 6],
# [ 8, 9, 10],
# [12, 13, 14]])
y
#array([[ 3],
# [ 7],
# [11],
# [15]])
y=y[:,0] #将y转化为向量
y
#array([ 3, 7, 11, 15])
强制类型转换
X=np.random.randint(0,100,size=(50,2)) #模拟共50个样本,每个样本2个特征
X=np.array(X,dtype=float)
矩阵运算
#想要L扩大两倍
L=np.arange(10)
L
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#方法一:
A=np.array([x*2 for x in L])
A
#array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
#方法二:
A=2*L #注意L是numpy创建的数组,不是一般的数组
Universal Function(单矩阵±*/)
abs、sin、cos、tan
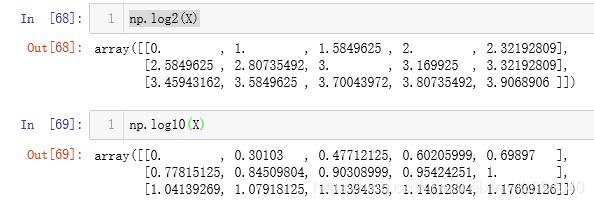
exp、power、log、log2、log10
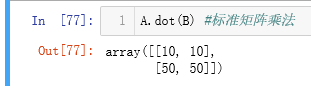
矩阵之间运算 ±*/、dot、.T
向量与矩阵之间运算 dot
向量转矩阵
方式1:转为mat
x
#array([8.09, 3.36])
np.mat(x)
#matrix([[8.09, 3.36]])
线性代数np.linalg
逆inv、伪逆pin
求逆矩阵:
invA=np.linalg.inv(A)
求伪逆矩阵:
pinvX=np.linalg.pinv(X)
模norm()
def direction(w): # 求单位矩阵
return w / np.linalg.norm(w)
聚合运算
numpy的聚合运算比python原生的快很多。
sum
向量
矩阵
min、max
求最大和最小可以使用numpy.min(对象),也可以使用对象.min()
积prod、mean、中位数median、百分位percentile
方差var、标准差std
比较
> 、== 、!=
count_nonzero
any、all、奇偶个数、&、|、非~
x[x
索引
最大值索引argmin、最小值索引argmax
排序sort、索引排序argsort、partition、argpartition
sort(x)返回排好序的值,不改变本身值。
x.sort()会改变本身值。
一维:
sort
 argsort
argsort
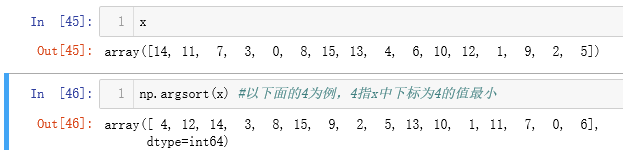 partition、argpartition
partition、argpartition

二维
sort
 argsort
argsort
 partition、argpartition
partition、argpartition

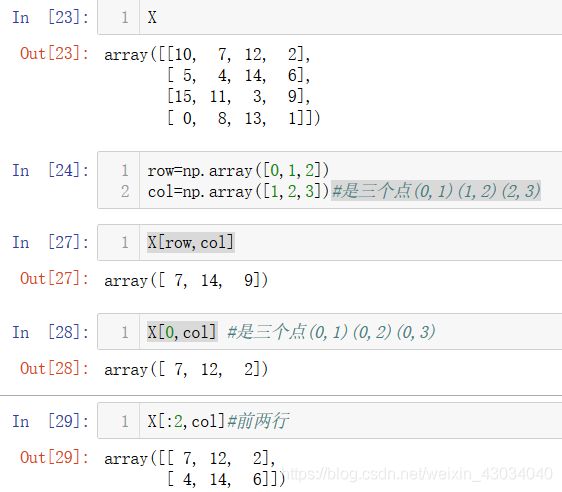
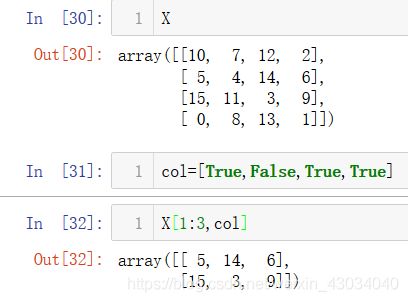
Fancy Indexing
matplotlib
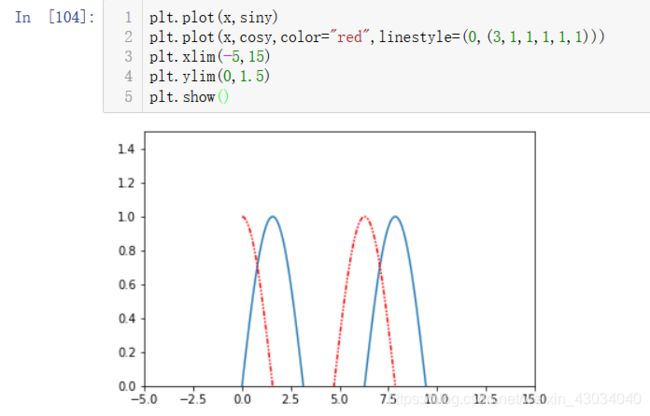
matplotlib包含很多绘图工具,用的较多的是它的子模块pyplot.
一条线
多条线
样式color、linestyle
color:
https://matplotlib.org/gallery/color/named_colors.html
linestyle:
https://matplotlib.org/gallery/lines_bars_and_markers/linestyles.html?highlight=linestyle

坐标轴范围xlim、ylim、axis
标签xlabel、ylable、label、title
xlabel、ylable是给x和y轴添加标注,label是给图中曲线增加标注。
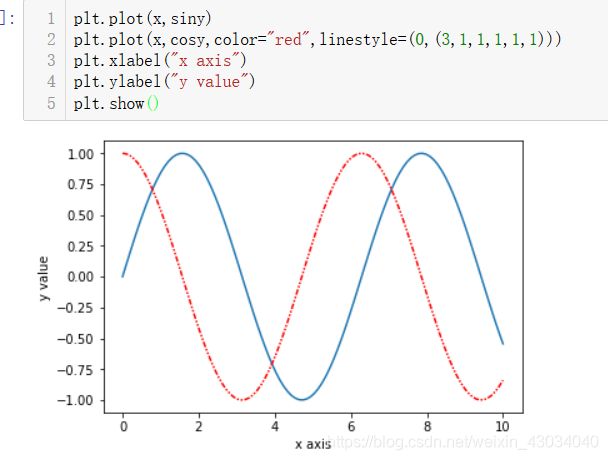 添加label
添加label
散点图(Scatter Plot)scatter
透明度 alpha
marker
参考文档:
https://matplotlib.org/api/markers_api.html?highlight=marker#module-matplotlib.markers
可视化
各类库
sklearn.datasets
提供样本数据集

make_moons
获得类似月亮形状的样本数据集
项目48
sklearn.preprocessing
预处理
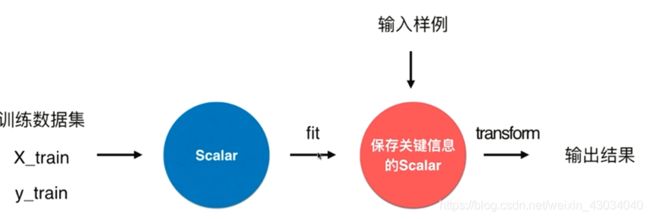
StandardScaler
使用训练样本来求均值和方差,用于数据归一化。
PolynomialFeatures
多项式回归。将1次的样本特征装换为多次。
pipeline
Pipeline
加上多项式回归后,数据就变得复杂了,要先处理多项式,还要归一化,再进行数据回归。所以出现了Pipeline,将这三个整合成一个。
可以参考第28个项目。
sklearn.model_selection
提供数据模型
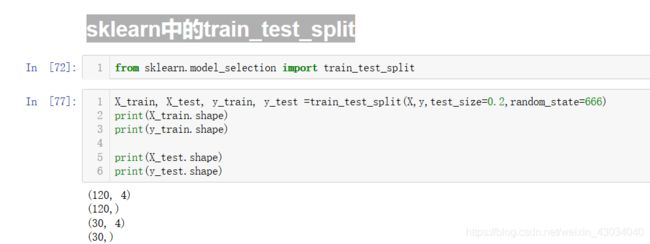
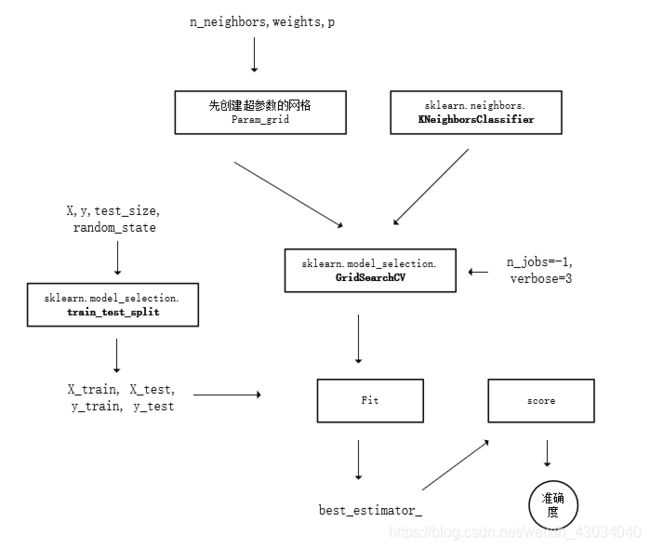
train_test_split
将样本的训练和测试按比例分离
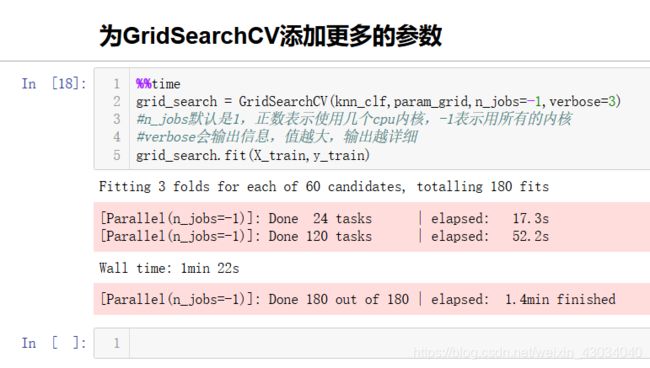
GridSearchCV
超参数网格搜寻,后面的CV是交叉验证
cross_val_score
交叉验证。
可以查看第32个项目。
sklearn.neighbors
提供训练模型
KNeighborsClassifier
kNN分类器,解决分类问题
KNeighborsRegressor
kNN 回归,解决回归问题
sklearn.metrics
提供衡量
mean_squared_error
mean_absolute_error
r2_score
计算R squre
confusion_matrix
混淆矩阵
项目41
precision_score
精准率
项目41
recall_score
查回率
项目41
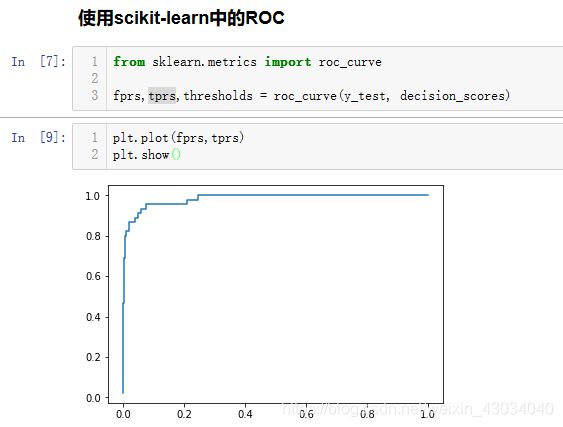
roc_curve
ROC曲线
项目45
roc_auc_score
ROC曲线的面积(即AUC),越大越好。(0.98是一个不错的值)
项目45
sklearn.linear_model
回归问题
LinearRegressor
使用批量梯度下降法的线性回归。
SGDRegressor
使用随机梯度下降法的线性回归。
Ridge
岭回归
项目33中使用
LASSO
LASSO回归
项目34中使用
和岭回归差不多
LogisticRegression
逻辑回归,逻辑回归也是和线性回归差不多的。
项目39
sklearn.multiclass
OneVsRestClassifier
分类问题的OvR方式
项目40
OneVsOneClassifier
分类问题的OvO方式
项目40
sklearn.decomposition
PCA
主成分。
项目25
sklearn.svm
支持向量机
LinearSVC
线性的SVM处理分类问题。
线性的支持向量分类(Linear suport vector classify)
项目47
SVC
多项式的 suport vector classify
可以自由添加核函数
项目48
LinearSVR
线性的SVM处理回归问题。
项目51
SVR
SVM解决回归问题
可以添加核函数
项目51,也可参考SVC
sklearn.tree
决策树
DecisionTreeClassifier
决策树分类
使用决策树解决分类问题
项目56
DecisionTreeRegressor
决策树回归
使用决策树解决回归问题
项目57
sklearn.ensemble
集成学习
VotingClassifier
少数服从多数的投票
项目60
BaggingClassifier
放回样本的集成学习
项目61
RandomForestClassifier
随机森林,整合了决策树和Bagging
项目63
ExtraTreesClassifier
极度随机决策树
在随机森林的基础上,进一步随机
项目63
BaggingRegressor
Bagging解决回归问题
RandomForestRegressor
随机森林解决回归问题
ExtraTreesRegressor
极度随机森林解决回归问题
AdaBoostClassifier
Ada增强分类器
项目64
GradientBoostingClassifier
Gradient增强分类器
项目64
AdaBoostRegressor
AdaBoost解决回归问题
GradientBoostingRegressor
GradientBoosting解决回归问题
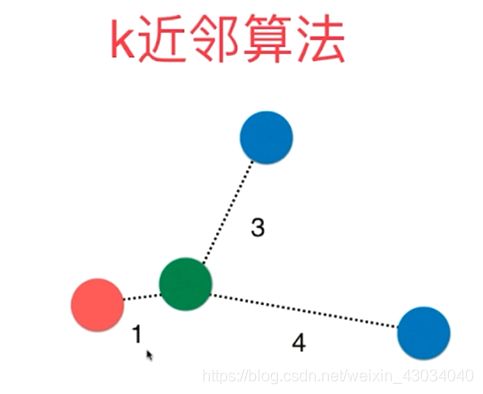
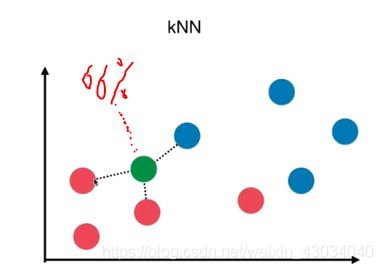
kNN-k邻近算法(k-Nearest Neighors)
k的大小自己取。
下图中,红色代表良性肿瘤,蓝色代表恶性肿瘤。
邻近绿色的点是三个恶性肿瘤,所以绿色可以判断为恶性肿瘤。

下图中,邻近绿色的点是1个恶性肿瘤,2个良性肿瘤,2大于1,所以绿色可以判断为良性肿瘤。
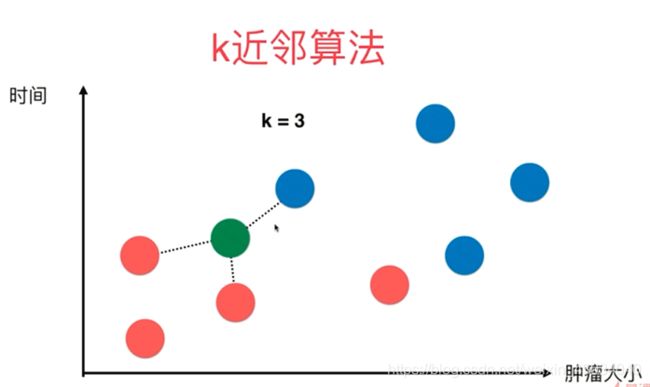
很简单,依次求出该点到各个点的距离,再取出前面几个即可。
使用scikit-learn中的kNN
训练和测试分离
实现1:jupter notebook(自己写的)
实现2:pycharm
import numpy as np
def train_test_split(X, y, test_ratio=0.2, seed=None):
"""将数据 X和y 按照test_ratio分割成X_train,X_test,y_train,y_test"""
assert X.shape[0] == y.shape[0], \
"the size of X must be equal to the size of y"
assert 0.0 <= test_ratio <= 1.0, \
"test_ratio must be valid"
if seed:
np.random.seed(seed)
shuffled_indexes = np.random.permutation(len(X))
test_size = int(len(X) * test_ratio)
test_indexes = shuffled_indexes[:test_size]
train_indexes = shuffled_indexes[test_size:]
X_train = X[train_indexes]
y_train = y[train_indexes]
X_test = X[test_indexes]
y_test = y[test_indexes]
return X_train, X_test, y_train, y_test
实现3:sklearn中的train_test_split
手写体识别
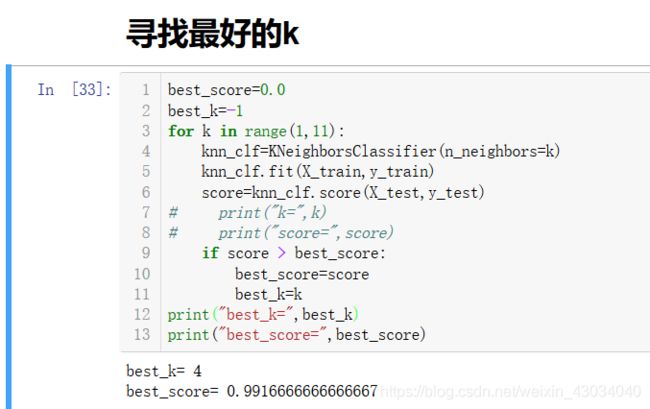
超参数
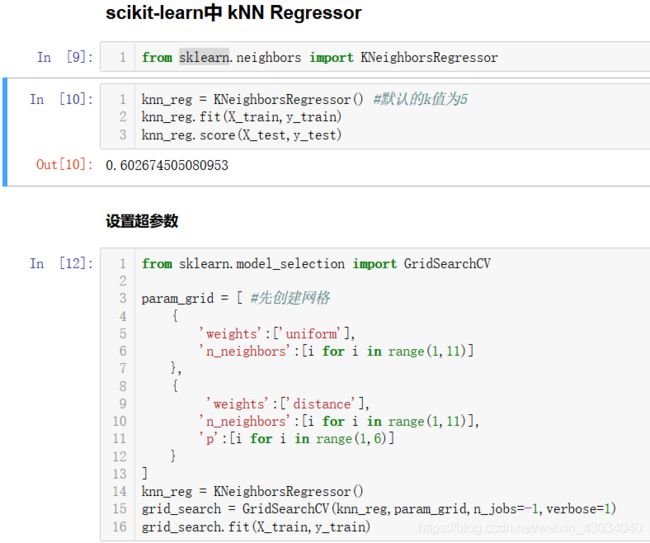
超参数: 在训练之前就需要确定的参数为超参数。例如,在KNN模型中的k.
模型参数:算法过程中学习的参数。
KNN中K
距离的权重
距离取倒数。
什么是距离
曼哈顿距离:
当p=1时,明可夫斯基距离=曼哈顿距离
当p=2时,明可夫斯基距离=欧拉距离
所以选择距离的p参数又成了超参数。
网格搜索
数据归一化
最值归一化、均值方差归一化
方式二:均值方差归一化 standardization (推荐)
测试数据归一化
优缺点
优点
解决分类问题,天然可以解决多分类问题。
思想简单,效果强大。
还可以解决回归问题。具体预测一个数值,例如房价多少。
使用kNN解决回归问题:

缺点
效率低下、高度数据相关、预测结果不具有可解释性、维数灾难

即使使用了优化,依旧效率低下。

不要以为10000维很大,100*100的图片就是1万维了
解决方法:降维
总结
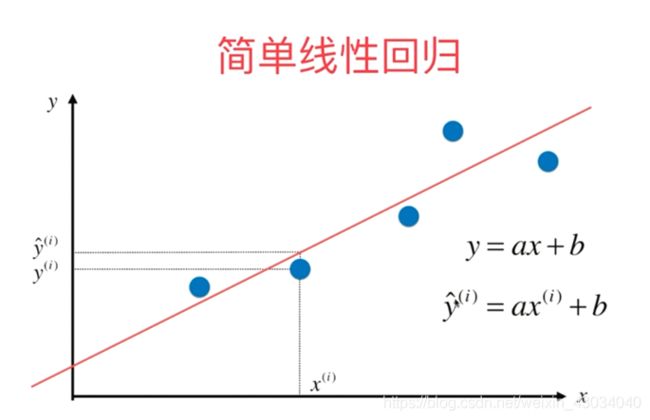
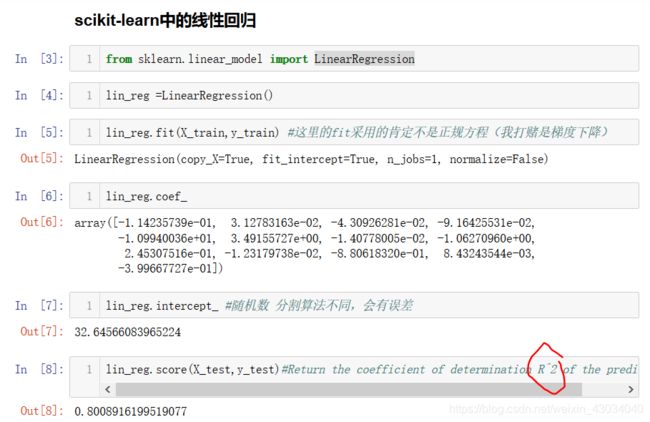
线性回归
简单线性回归(一个特征值)
最小二乘法过程
向量化运算
衡量线性回归的指标
标准1:均方误差MSE
标准2:均方误差跟RMSE
标准3:平均绝对误差MAE
比较 RMSE和MAE
RMSE放大了误差较大的值
例如误差是10和2
RMSE =(100+4)/2 再开方
MAE = (10+2)/2
标准4(最佳):R Squared
分母是直接粗暴的取平均值,也就是说,我直接将预测结果定为平均值。
分子是我们使用模型预测的差值。

多元线性回归
正规方程

思路是和最小二乘法一样的也是求导求极值的过程,只不过是在整个矩阵上。但难度超过了本科的要求



自我实现线性回归
sklearn中的线性回归
sklearn中的 kNN 回归
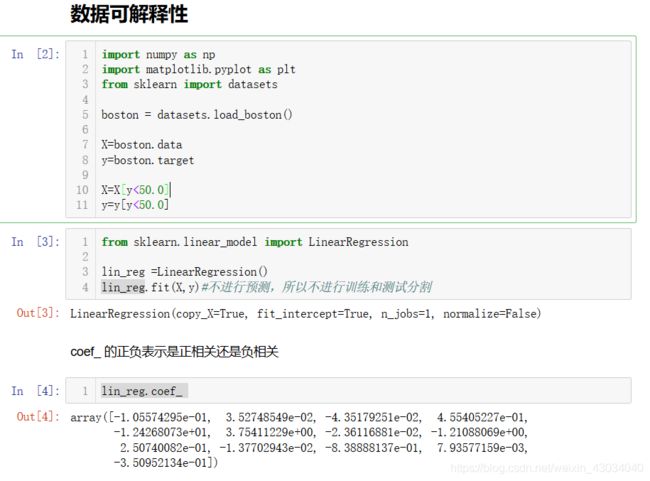
数据可解释性
例如发现:
RM越大,价格越高。解释了房屋面积对房价的影响。
CHAS为1,价格越高。解释了是否临近泰晤士河对房价的影响。
NOX越高,房价月底。解释了NO气体越浓,房价月底。
例如:通过NOX又可以取找附近是否有工厂,从而进行优化。
梯度下降法
可能会遇到的问题:


eta一般取0.01是可以的,但出现异常的情况,可以把图像显示出来查看。
一个theta是求导数,多个theta是求偏导数
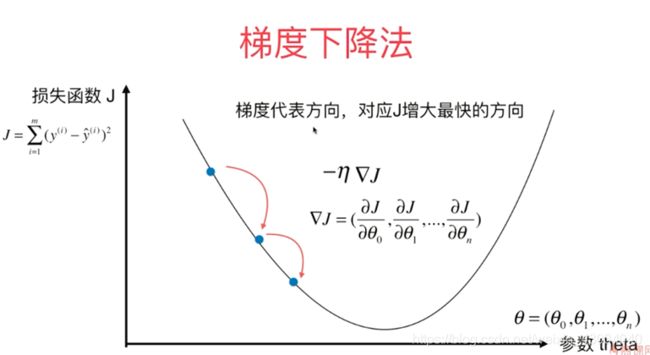


 14-Gradient-Descent-Simulation.ipynb
14-Gradient-Descent-Simulation.ipynb
向量化
X_b.T.dot(X_b.dot(theta)-y)* 2 / len(X_b)
16-Vectorize-Gradient-Descent.ipynb
数据归一化
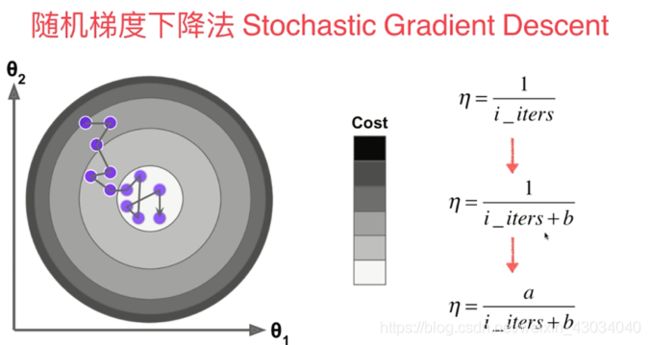
批量和随机 下降法
学习率需要逐渐的减小。上图中的a,b决定了eta的变化,所a,b是两个超参数。但在此不做过多讨论。a=5,b=50
17-Stochastic-Gradient-Descent.ipynb
18-SDG-in-scikit-learn.ipynb
关于梯度的调试
取theta旁边的两个点来代替求导过程是很好理解的,但是计算的复杂度大大增加。
因为每求一个theta的导数都需要带入两遍的J(theta).
但可以使用少数的数据进行调试
先使用调试的求导方式,虽然耗时长,但会得到正确的结果。再通过数学推导的求导方式来求解。
这里面的调试求导方法适用于所有函数的求导。

19-Gradient-Debugging.ipynb
总结
批量梯度下降法速度慢,但稳定。
随机梯度下降法速度快,但不稳定。
从而引申出小批量梯度下降法。
随机梯度下降法:每次求导只提取一个样本
小批量梯度下降法:每次求导提取K(例:10到20)个样本
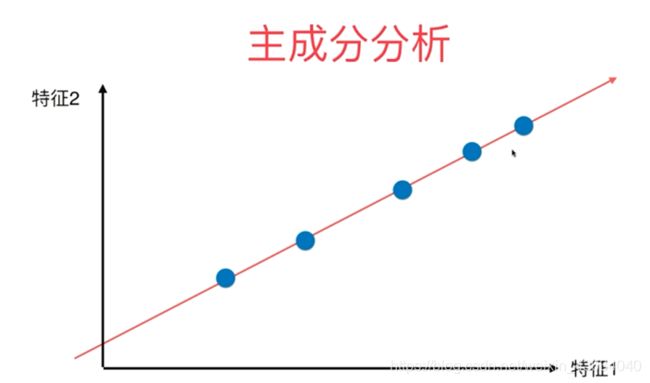
主成分分析 PCA
Principal Component Analysis
原理

要使方差尽可能大,因为方差越大代表着数据越分散,越能体现特征。

步骤:
使用 X*w代替 Xproject
使用梯度上升法
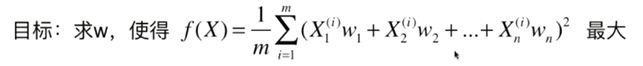

X1w1+X2w2 …上述就是点乘的问题,等价于下面的



上面的式子很好推,花三分钟就推出来了。
实现
这里使用批量梯度上升法,同理,还可以使用随机梯度上升法和小批量梯度上升法。
20-Implement-PCA-in-BGA.ipynb
前n个主成分
求出一个主成分后,当要求下一个主成分时,需要消除之前的那个主成分的影响。
下图中,蓝线是一个主成分。当求下一个主成分时,需要将样本映射到绿线上。再来求下一个主成分。
依次类推。


21-Getting-First-N-Component.ipynb
高维向低维映射
数据映射
22-Data-Projection.ipynb
scikit-learn中的PCA
23-PCA-in scikit-learn.ipynb
MNIST 7万手写体识别
PCA实现降噪
降维的时候丢失信息,其实丢失了大部分的噪音。
25-PCA-for-noice-reduction.ipynb
人脸识别和特征脸

X中的每行是一个样本,可以是一个人脸图像样本。
W中的每行,也可以理解是一个人脸,称为特征脸。每个特征脸对应一个主成分。
W中的每一行的维度是和X中的样本一样的。
特征脸:eigen face
特征值:eigen value
特征向量:eigen vector
多项式回归
简单示例

多项式回归的问题本质还是线性回归。是原有特征的组合。
上一章的PCA是降维,而这个是升维。
27-Polynomial-Regression.ipynb
scikit-learn的多项式回归和Pipeline
算是数据预处理的过程。

加上多项式回归后,数据就变得复杂了,要先处理多项式,还要归一化,再进行数据回归。所以出现了Pipeline,将这三个整合成一个。

28-Polynomial-Regression.ipynb
过拟合和欠拟合
欠拟合:

过拟合:
较好的拟合了训练样本集。
但是不能拟合测试样本集。
过多的表达了数据间的噪音关系。
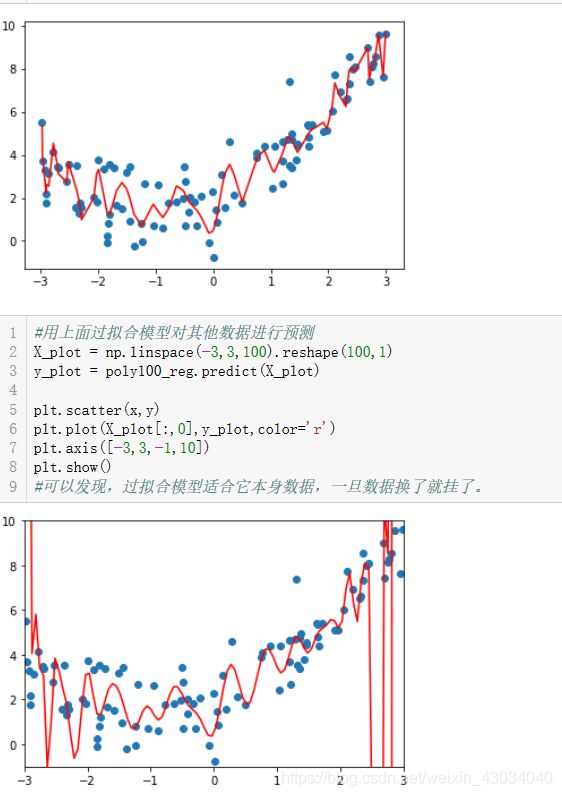
29-Underfitting-and-Overfitting.ipynb
过拟合对原来的样本点能够很好的拟合,但一旦来了新的样本点,就无法进行性预测了。
模型的范化能力非常的差。
分离训练集和测试集的意义
从欠拟合到过拟合的过程。
学习曲线
随着训练样本的逐渐增多,算法训练出的模型的表现能力。
下图中横坐标表示训练样本数,纵坐标表示均方误差跟。

 31-Learning-Curve.ipynb
31-Learning-Curve.ipynb
验证数据集
面临问题:
一直用测试数据集进行评判,会出现针对特定测试数据集过拟合。例如:当通过训练数据训练好模型后,用测试数据集进行测试,一旦不理想,就换个超参数。这样一直是围绕测试数据集打转。也就是会根据测试数据集进行调参。测试数据集不应该出现在模型塑造的过程中。
解决方法:

这样又有一个问题:
验证数据集如何获取?
是随机给吗?
如果验证数据集中出现极端数据怎么办?
解决方法是交叉验证
交叉验证
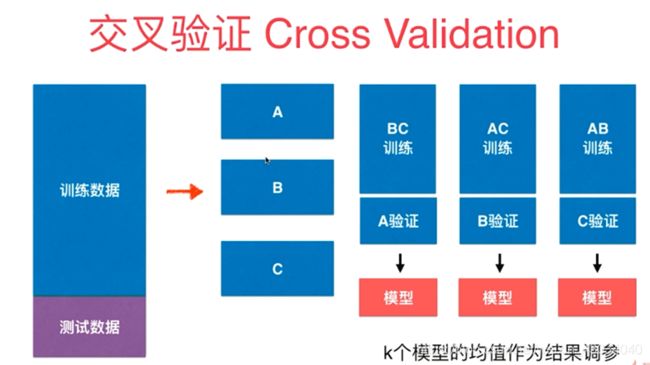
交叉验证的过程中,是将各个模型的验证结果求平方,这样就避免了个别极端样本的影响
32-Validation-and-Cross-Validation.ipynb

如果有m个样本,k取m-1这种极端的情况,那么称为留一法。
留一法运行时间特别缓慢,但是能够充分反映样本的性能。有时,发表论文时会使用到。一般不会用到。

偏差和方差的权衡
偏差 : bias
方差: variance
越分散,方差越大。
越偏离,偏差越大。
偏差
方差
解决高方差(过拟合)
不使用验证集会过拟合,这是对测试数据集的过拟合。
正则化

终于理解了正则化的含义,吼吼。
出现过拟合时,theta是异常的,会出现特别大的值。

正则化就是对theta进行惩罚。
开发经验
开发经验:
岭回归是精准的,如果计算量承受的住的话,就是用岭回归。
当特征特别多(岭回归无法使θ为0,无法减少特征值),计算量承受不住,优先使用弹性网。
弹性网既有LASSO的特征选择优点,又不至于使过多的θ为0。
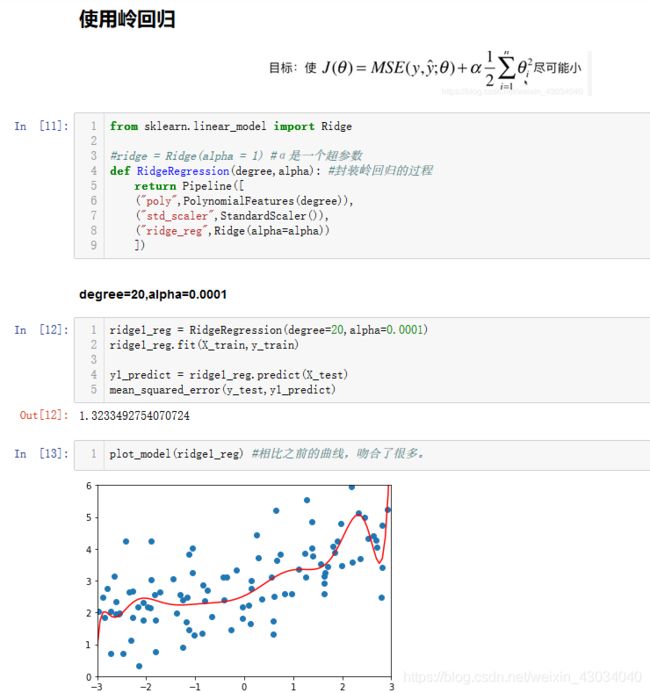
方式1:岭回归 ridge regression
- theta0 不需要正则化,因为theta0 是截距。
只决定曲线的高低,不形象是否过拟合。
- 取二分之一是为了求导方便
- α是一个超参数 。α为0时,等同于没有正则化,α很大时,前面的MSE就无意义了。
33-Ridge-Regression.ipynb
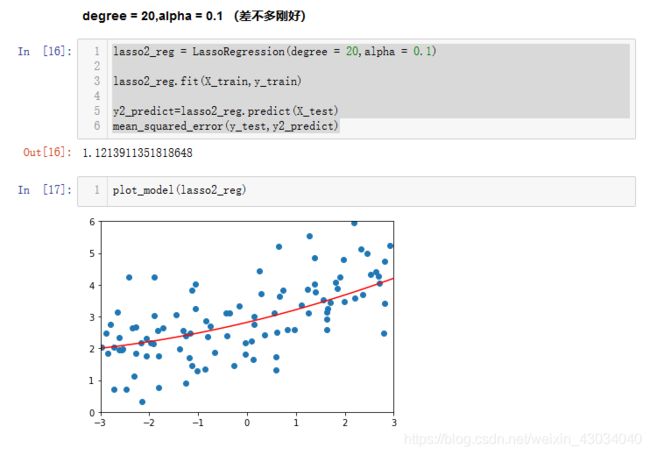
方式2:LASSO Regularization
比较Ridge和LASSO
Ridge会让theta变小,但不会让theta变为0。
LASSO会让部分theta变为0


在 ridge回归中,theta接近0的过程中,每个theta都不断变小,但不会为0
岭回归的三维图:
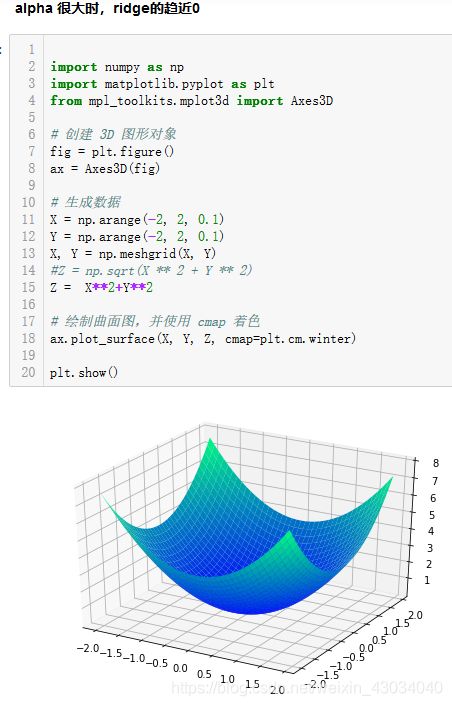

在 LASSO回归中,theta接近0的过程中,各个偏导数导数是1(或-1,反正都一样),那么在某个时刻,部分的theta会变为0,但其他的没有变为0.这就是上图中的拐点部分。
LASSO回归的三维图:
优缺点
因为LASSO会使部分的theta变为0,所以从计算的准确度而言,使用ridge较为准确。
但是当特征特别多的时候,LASSO可以让特征数变小。
开发经验:
岭回归是精准的,如果计算量承受的住的话,就是用岭回归。
当特征特别多(岭回归无法使θ为0,无法减少特征值),计算量承受不住,优先使用弹性网。
弹性网既有LASSO的特征选择优点,又不至于使过多的θ为0。
数学思想
数学相像。
L1正则,L2正则,L0正则

Lp范数是对任意一个样本的所有特征进行运算。
p=1是L1范数,等价于曼哈顿距离。
p=2是L2范数,等价于欧拉距离。
Ln正则项只是在Lp的基础上不做开p次方。
一般不用n大于3的正则项,但数学理论上存在的。

L0正则项是指使θ的个数越少,当然很少用。
实际使用L1取代,因为L0正则的优化是一个NP难的问题。使用L1(LASSO)就会使部分theta变为0,实现了L0想要达到的目的
弹性网 Elastic Net
正则项使用 是 L1正则 + L2正则。同时拥有了两者的优势。

上式中的r有时一个超参数,表示两种超参数的比例。前面的是r,后面的是1-r后面的1/2是对付平方导数的(不懂的话,拖出去打死就行)
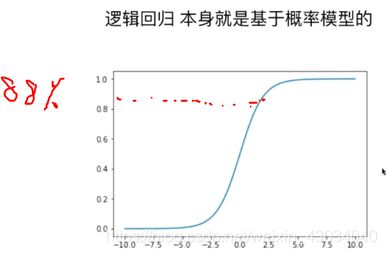
逻辑回归
从下图可以发现,算法不是越复杂越好。
算法是越适合越好。


逻辑回归也是回归,它是在最后根据概率来判断是否。
逻辑回归本身只能解决二分类,当然,是可以处理的。
sigmod
代价函数
求导过程
sigmod(t)求导:
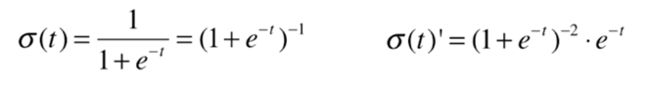
带入到log()函数进行求导:

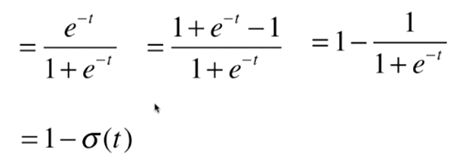
即:
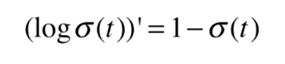
现在开始求后半部分:
先是log求导:

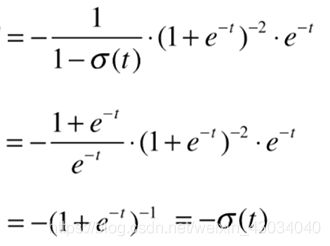
再进行整个后半部分的求导:

最后进行前后合并。


和线性回归是一样的。同样的方式进行向量化。
求导结果
逻辑回归用例
鸡尾花二分类。
先进行封装。
36-Implement-Logistic-Regression.ipynb
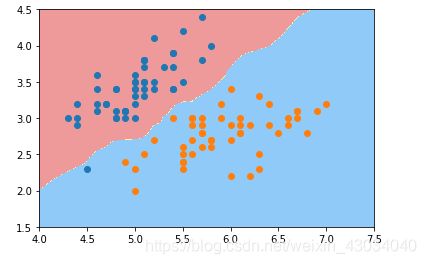
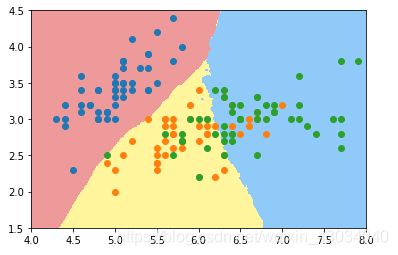
决策边界
逻辑回归边界
kNN决策边界
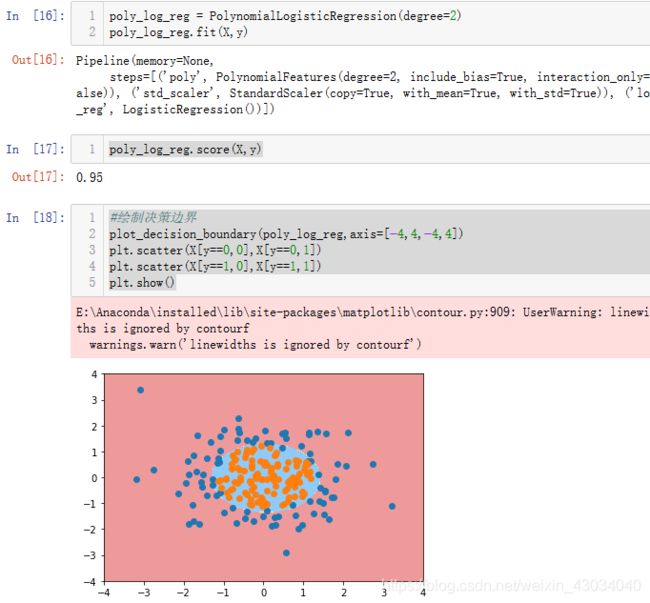
使用多项式特征
使用管道
过拟合
正则化

我们不知道样本是怎么样的,所以要使用超参数网 degree,C,penalty 都是超参数。
39-Logistic-Regression-in-sklearn.ipynb
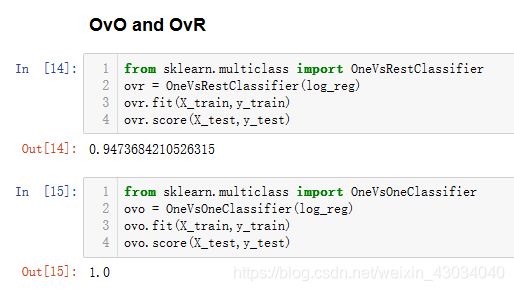
多分类
OvA=one vs all =OvR=one vs rest

slinear_model 中的LogisticRegression
OneVsRestClassifier和OneVsOneClassifier
分类算法的评价
对于线性回归问题,评价标准有MSE、RMSE、MAE、R Square.
但是对于逻辑回归的评价标准,只有一个准确度(accuracy_score)是不够的。
问题
混淆矩阵 Confusion Matrix
精准率和召回率
前一个字母表示预测正确和错误,后一个字母表示预测值。
精准率:医生说100个人有病,其中真实有病的为36人,精准率为36%。
召回率:房间里有100个人有病,医生说有36人有病,召回率是36%
41-implement-Confusion-Matrix-Precision-and-Recall.ipynb
F1 Score
精准率和召回率的选择是视情况而定。
例如
股票选择:高精准率。选出的股票一定要涨。如果我没买的股票涨了,对我也没有损失。
医生:高召回率。有病的人来到医院一定要被检测出来。如果没病却检测出有病,只要进一步验证即可。
也可以同时兼顾这两个指指标。例如F1 Score
调和平均值比平均值要好。
平均值:一个接近0,一个接近1,平均值为0.5。
调和平均值:一个接近0,一个接近1,调和平均值接近0。这就是优点。
42-F1-Score.ipynb
Precision-Recall的平衡
精准率和召回率是相互矛盾的。很难将两个都调好

不管边界往哪里移动,精准率和召回率都会相互影响。
决策边界的修改

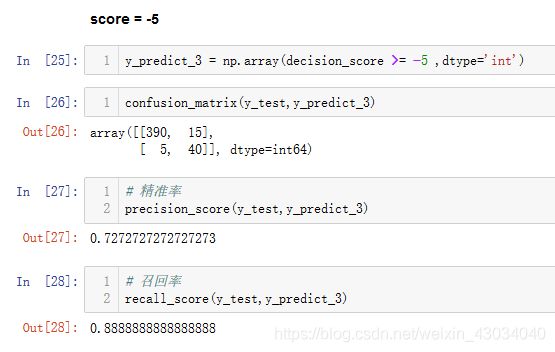
43-Precision-Recall-Trade-Off.ipynb
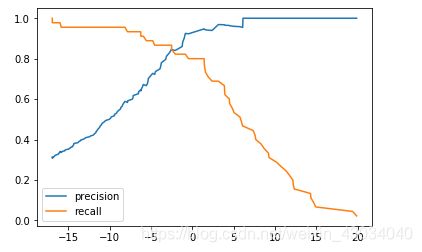
PR曲线

44-Precision-Recall-Curve.ipynb
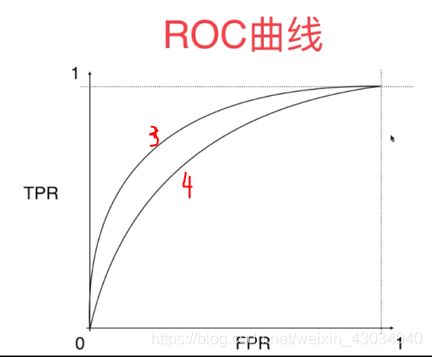
Precision-Recall曲线
上面的PR曲线大致是下图这样。下图两条PR曲线对应2个模型。明显曲线1对应的模型较好。
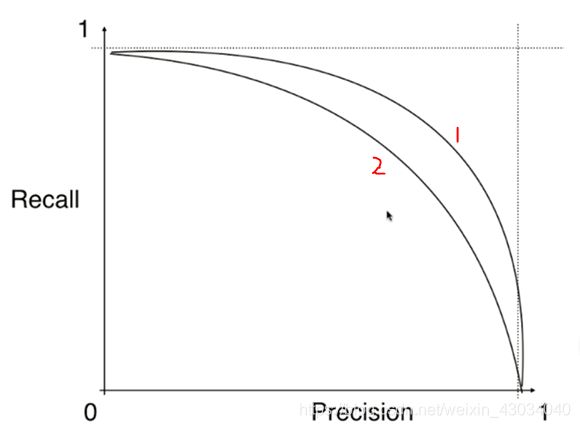
ROC曲线
Receoiver Operation Characteristic Curve
描述真正例率TPR和 假正例率FPR之间的关系
TPR = 召回率
45-ROC.ipynb
多分类问题
多分类的精准率和召回率
多分类的混淆矩阵
 46-Confusion-Matrix-in-Multi-class.ipynb
46-Confusion-Matrix-in-Multi-class.ipynb
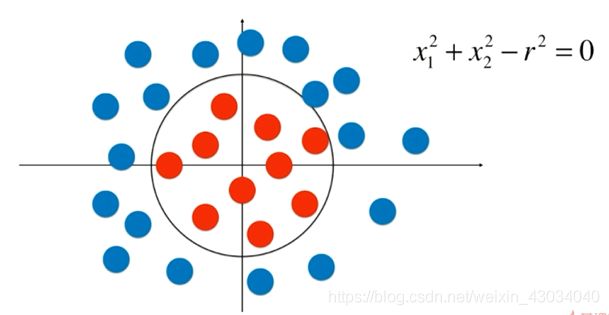
支撑向量机 SVM
由于SVM底层实现复杂,学会使用即可。
Support Vector Machine
决策边界可以有很多条可以适用。
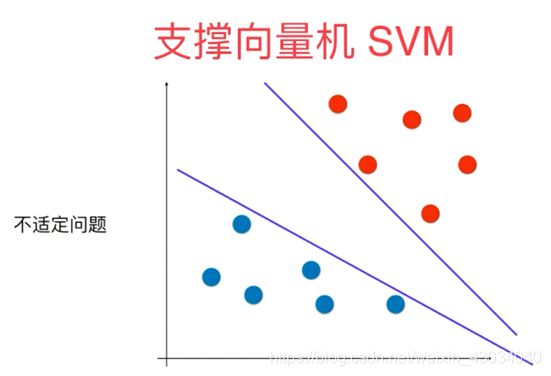
想让决策边界离红色样本越远,同时离蓝色样本也越远。

SVM思想是不仅考虑划分现有的样本,还考虑了未来的情况。
假如数据刚好是线性可分的。(当然,大部分都是不可分的,哪有一条直线刚好可以将样本分为两部分!)

线性可分:Hard Margin SVM
线性不可分: Soft Margin SVM
线性可分 Hard Margin SVM
将Wd bd重新用W b表示
线性不可分 Soft Margin SVM
错误的决策边界:
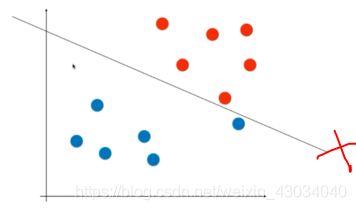
线性不可分:

从而引申出soft margin SVM:


C值越大,给的容错率越小,越接近hard margin SVM
sklearn 中的SVM
hard SVM
soft SVM
47-SVM-in-scikit-learn.ipynb
多项式
方式1:使用PolynomialFeatures增加degree

方式2:使用多项式核函数的SVM

48-Polynomial-Features-in-SVM.ipynb
核函数
之前提高阶数需要使用多项式特征添加degree。
使用核函数就是用来取代这个步骤的。交给核函数来处理。

上述推导公式不做要求。
相较于使用之前的多项式特征先变化degree,使用核函数能够降低计算量和存储空间(之前的degree上升,需要大量的存储空间)
核函数不是SVM的专属,他也是一种技巧。只不过在SVM中用的比较多。
多项式核函数
c和d就是超参数

sklearn中提供的SVC中就有kernel选择。
线性核函数
多项式核函数就是为了为线性函数添加degree.
那线性核函数就是没有degree的核函数。
高斯核函数
高斯函数属于正态分布的一种。
也叫RBF核(Radial Basis Function Kernel)、径向基函数
高斯核函数对每个样本的变形是很复杂的,变形后的结果是简单的。(就是上面的式子)
高斯核函数将每一个样本点映射到一个无穷维的特征空间。
多项式特征就是将原来线性不可分的数据线性可分。
例如:下面的线性不可分

如果把原来的转换为平方。那么久变成下面的:

这样就线性可分了。
高斯核函数做的同样也是这件事。


49-What-is-RBF-Kernel.ipynb

很容易发现,高斯是很耗计算量的。
如果初始的样本数据维度n很高,但样本数据数目m不大,那么使用高斯核函数就比较划算。例如自然语言处理。

高斯函数中,
u代表均值,
σ代表标准差,越小,图形越窄,越高。
而γ的关系和σ是呈导数的关系。
50-RBF-Kernel-in-scikit-learn.ipynb
SVM思路还可解决回归问题
和分类问题刚好相反,回归问题要求在margin里的样本点要越多越好。
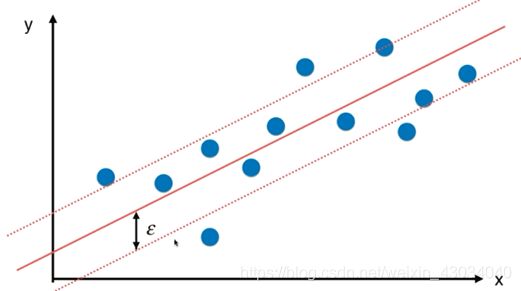
epsilon 也是一个超参数。

决策树
52-What-is-Decision-Tree.ipynb
信息熵


左边的随便给你一个样本,你完全无法估计大致在哪个类里。确定性低
但右边可以确定,有很大的概率在第三个类。确定性高
53-Entropy.ipynb
使用信息熵寻找最优分化

54-Entropy-Split-Simulation.ipynb
基尼系数
两个结果值的分布对应的基尼系数值:
55-Gini-index.ipynb
两者比较
CART
Classification And Regression Tree
既可以解决回归问题,也可以解决分类问题。

生成的是二叉树。
sklearn 就是通过这种方法实现决策树的。当然还有其他,ID3,C4.5,C5.0

非常容易过拟合(所有的非参数学习都会面临过拟合问题)
剪枝需要降低复杂度,解决过拟合问题。
解决分类问题
 56-CART-and-Decision-Tree-Classifier.ipynb
56-CART-and-Decision-Tree-Classifier.ipynb
解决回归问题
思路是在分类问题的基础上取绝对值。
一个样本来到某个叶子节点,返回叶子节点中样本的平均值。
57-Decision-Tree-Regressor.ipynb
决策树的局限性
决策树并不推荐单独使用。
结合随机森林会有很好的效果。
1.只能横竖划分
2.对个别数据敏感
改变一个样本就可能改变整个模型。
58-Problem-of-Decision-Tree.ipynb
集成学习
hard voting (一人一票)
soft voting (权重)
一人一票肯定不好,专业人士应该具有的权重更大。

带有权重的预测

这要每个模型都能估计概率。
svm算法是用来搞决策边界的,但sklearn中提供求概率的函数(计算复杂,不做底层了解)

很多很多个模型
Bagging(bootstrap放)和Pasting(不放)
如果有500个样本,不放回取样的话,只能训练5个模型。放回取样可以训练很多很多个模型。
OOB (Out-of-Bag)
62-oob-和更多Bagging相关.ipynb
取出来又放回去,这样平均大概37%是没有取到的。可以直接使用这37%的样本作为测试数据集。而不需要测试和训练集分离。
简单使用
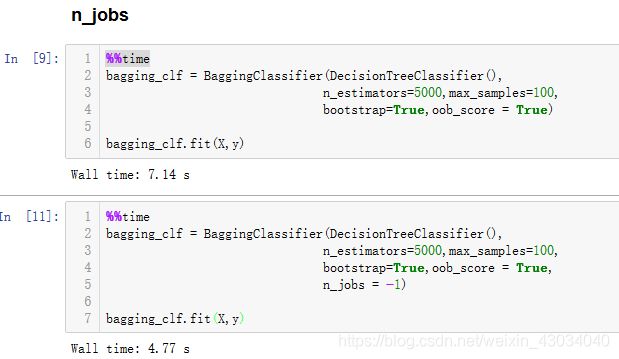
多线程运行
随机取样
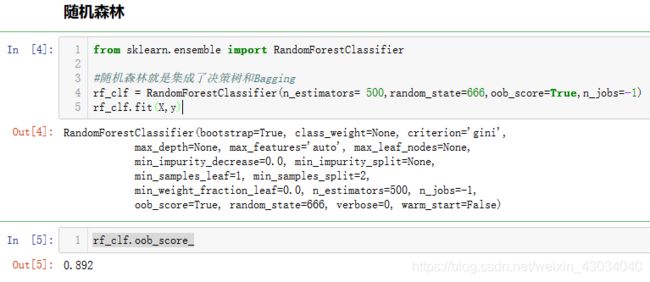
随机森林
有很多的决策树模型,就形成了决策树森林。
随机森林就是集成了决策树和Bagging
63-Random-Forest-Trees-and-Extra-Trees.ipynb
随机森林
极度随机森林

使用随机的特征和阀值看起来你很扯淡,但不要忘了集成学习只需要求模型的准确度高于50%。
解决回归问题
和分类问题差不多。有空自己学习。
Boosting(增强)
同样集成多个模型。
但和Bagging不同,它的每个模型不是独立的,而是每个模型都在增强(Boosting)整体的效果。
Ada Boosting
 预测对了的样本在下一次的训练中权重会降低。
预测对了的样本在下一次的训练中权重会降低。
可以发现每个模型都在弥补上一个模型的错误。
Gradient Boosting
64-Boosting.ipynb
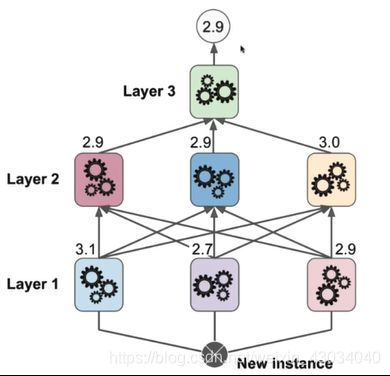
Stacking

思想:多个模型输出结果,再把结果作为输入创建新的一个模型(说好的建国之后不许套娃!!)
- 拆分样本,分为两份
- 将第一份样本作为训练集,训练上面的三个模型
- 将第二份样本作为测试集,每个样本得到三个预测值
- 将第二份样本和对应的预测值组合成新的样本,投入到新的模型训练中。
sklearn文档的使用
user guide
user guide相当于一本机器学习的书,有兴趣可以通读
user guide的每一部分先是介绍,点击着重字体会进入到API的具体使用。
API
API是每个可以使用的函数。也就是我们用到的东西。
进入API后可以使用网页查找找到具体的内容
扩展
贝叶斯算法
神经网络
数据预处理
索引
最大值索引argmin、最小值索引argmax
排序sort、索引排序argsort、partition、argpartition
sort(x)返回排好序的值,不改变本身值。
x.sort()会改变本身值。
一维:
sort
 argsort
argsort
 partition、argpartition
partition、argpartition

二维
sort
 argsort
argsort
![]() partition、argpartition
partition、argpartition

Fancy Indexing
matplotlib
matplotlib包含很多绘图工具,用的较多的是它的子模块pyplot.
一条线
多条线
样式color、linestyle
color:
https://matplotlib.org/gallery/color/named_colors.html
linestyle:
https://matplotlib.org/gallery/lines_bars_and_markers/linestyles.html?highlight=linestyle

坐标轴范围xlim、ylim、axis
标签xlabel、ylable、label、title
xlabel、ylable是给x和y轴添加标注,label是给图中曲线增加标注。
 添加label
添加label
散点图(Scatter Plot)scatter
透明度 alpha
marker
参考文档:
https://matplotlib.org/api/markers_api.html?highlight=marker#module-matplotlib.markers
可视化
各类库
sklearn.datasets
提供样本数据集

make_moons
获得类似月亮形状的样本数据集
项目48
sklearn.preprocessing
预处理
StandardScaler
使用训练样本来求均值和方差,用于数据归一化。
PolynomialFeatures
多项式回归。将1次的样本特征装换为多次。
pipeline
Pipeline
加上多项式回归后,数据就变得复杂了,要先处理多项式,还要归一化,再进行数据回归。所以出现了Pipeline,将这三个整合成一个。
可以参考第28个项目。
sklearn.model_selection
提供数据模型
train_test_split
将样本的训练和测试按比例分离
GridSearchCV
超参数网格搜寻,后面的CV是交叉验证
cross_val_score
交叉验证。
可以查看第32个项目。
sklearn.neighbors
提供训练模型
KNeighborsClassifier
kNN分类器,解决分类问题
KNeighborsRegressor
kNN 回归,解决回归问题
sklearn.metrics
提供衡量
mean_squared_error
mean_absolute_error
r2_score
计算R squre
confusion_matrix
混淆矩阵
项目41
precision_score
精准率
项目41
recall_score
查回率
项目41
roc_curve
ROC曲线
项目45
roc_auc_score
ROC曲线的面积(即AUC),越大越好。(0.98是一个不错的值)
项目45
sklearn.linear_model
回归问题
LinearRegressor
使用批量梯度下降法的线性回归。
SGDRegressor
使用随机梯度下降法的线性回归。
Ridge
岭回归
项目33中使用
LASSO
LASSO回归
项目34中使用
和岭回归差不多
LogisticRegression
逻辑回归,逻辑回归也是和线性回归差不多的。
项目39
sklearn.multiclass
OneVsRestClassifier
分类问题的OvR方式
项目40
OneVsOneClassifier
分类问题的OvO方式
项目40
sklearn.decomposition
PCA
主成分。
项目25
sklearn.svm
支持向量机
LinearSVC
线性的SVM处理分类问题。
线性的支持向量分类(Linear suport vector classify)
项目47
SVC
多项式的 suport vector classify
可以自由添加核函数
项目48
LinearSVR
线性的SVM处理回归问题。
项目51
SVR
SVM解决回归问题
可以添加核函数
项目51,也可参考SVC
sklearn.tree
决策树
DecisionTreeClassifier
决策树分类
使用决策树解决分类问题
项目56
DecisionTreeRegressor
决策树回归
使用决策树解决回归问题
项目57
sklearn.ensemble
集成学习
VotingClassifier
少数服从多数的投票
项目60
BaggingClassifier
放回样本的集成学习
项目61
RandomForestClassifier
随机森林,整合了决策树和Bagging
项目63
ExtraTreesClassifier
极度随机决策树
在随机森林的基础上,进一步随机
项目63
BaggingRegressor
Bagging解决回归问题
RandomForestRegressor
随机森林解决回归问题
ExtraTreesRegressor
极度随机森林解决回归问题
AdaBoostClassifier
Ada增强分类器
项目64
GradientBoostingClassifier
Gradient增强分类器
项目64
AdaBoostRegressor
AdaBoost解决回归问题
GradientBoostingRegressor
GradientBoosting解决回归问题
kNN-k邻近算法(k-Nearest Neighors)
k的大小自己取。
下图中,红色代表良性肿瘤,蓝色代表恶性肿瘤。
邻近绿色的点是三个恶性肿瘤,所以绿色可以判断为恶性肿瘤。

下图中,邻近绿色的点是1个恶性肿瘤,2个良性肿瘤,2大于1,所以绿色可以判断为良性肿瘤。

很简单,依次求出该点到各个点的距离,再取出前面几个即可。
使用scikit-learn中的kNN
训练和测试分离
实现1:jupter notebook(自己写的)
实现2:pycharm
import numpy as np
def train_test_split(X, y, test_ratio=0.2, seed=None):
"""将数据 X和y 按照test_ratio分割成X_train,X_test,y_train,y_test"""
assert X.shape[0] == y.shape[0], \
"the size of X must be equal to the size of y"
assert 0.0 <= test_ratio <= 1.0, \
"test_ratio must be valid"
if seed:
np.random.seed(seed)
shuffled_indexes = np.random.permutation(len(X))
test_size = int(len(X) * test_ratio)
test_indexes = shuffled_indexes[:test_size]
train_indexes = shuffled_indexes[test_size:]
X_train = X[train_indexes]
y_train = y[train_indexes]
X_test = X[test_indexes]
y_test = y[test_indexes]
return X_train, X_test, y_train, y_test
实现3:sklearn中的train_test_split
手写体识别
超参数
超参数: 在训练之前就需要确定的参数为超参数。例如,在KNN模型中的k.
模型参数:算法过程中学习的参数。
KNN中K
距离的权重
距离取倒数。
什么是距离
曼哈顿距离:
当p=1时,明可夫斯基距离=曼哈顿距离
当p=2时,明可夫斯基距离=欧拉距离
所以选择距离的p参数又成了超参数。
网格搜索
数据归一化
最值归一化、均值方差归一化
方式二:均值方差归一化 standardization (推荐)
测试数据归一化
优缺点
优点
解决分类问题,天然可以解决多分类问题。
思想简单,效果强大。
还可以解决回归问题。具体预测一个数值,例如房价多少。
使用kNN解决回归问题:

缺点
效率低下、高度数据相关、预测结果不具有可解释性、维数灾难

即使使用了优化,依旧效率低下。

不要以为10000维很大,100*100的图片就是1万维了
解决方法:降维
总结
线性回归
简单线性回归(一个特征值)
最小二乘法过程
向量化运算
衡量线性回归的指标
标准1:均方误差MSE
标准2:均方误差跟RMSE
标准3:平均绝对误差MAE
比较 RMSE和MAE
RMSE放大了误差较大的值
例如误差是10和2
RMSE =(100+4)/2 再开方
MAE = (10+2)/2
标准4(最佳):R Squared
分母是直接粗暴的取平均值,也就是说,我直接将预测结果定为平均值。
分子是我们使用模型预测的差值。

多元线性回归
正规方程

思路是和最小二乘法一样的也是求导求极值的过程,只不过是在整个矩阵上。但难度超过了本科的要求



自我实现线性回归
sklearn中的线性回归
sklearn中的 kNN 回归
数据可解释性
例如发现:
RM越大,价格越高。解释了房屋面积对房价的影响。
CHAS为1,价格越高。解释了是否临近泰晤士河对房价的影响。
NOX越高,房价月底。解释了NO气体越浓,房价月底。
例如:通过NOX又可以取找附近是否有工厂,从而进行优化。
梯度下降法
可能会遇到的问题:


eta一般取0.01是可以的,但出现异常的情况,可以把图像显示出来查看。
一个theta是求导数,多个theta是求偏导数



 14-Gradient-Descent-Simulation.ipynb
14-Gradient-Descent-Simulation.ipynb
向量化
X_b.T.dot(X_b.dot(theta)-y)* 2 / len(X_b)
16-Vectorize-Gradient-Descent.ipynb
数据归一化
批量和随机 下降法
学习率需要逐渐的减小。上图中的a,b决定了eta的变化,所a,b是两个超参数。但在此不做过多讨论。a=5,b=50
17-Stochastic-Gradient-Descent.ipynb
18-SDG-in-scikit-learn.ipynb
关于梯度的调试
取theta旁边的两个点来代替求导过程是很好理解的,但是计算的复杂度大大增加。
因为每求一个theta的导数都需要带入两遍的J(theta).
但可以使用少数的数据进行调试
先使用调试的求导方式,虽然耗时长,但会得到正确的结果。再通过数学推导的求导方式来求解。
这里面的调试求导方法适用于所有函数的求导。

19-Gradient-Debugging.ipynb
总结
批量梯度下降法速度慢,但稳定。
随机梯度下降法速度快,但不稳定。
从而引申出小批量梯度下降法。
随机梯度下降法:每次求导只提取一个样本
小批量梯度下降法:每次求导提取K(例:10到20)个样本
主成分分析 PCA
Principal Component Analysis
原理

要使方差尽可能大,因为方差越大代表着数据越分散,越能体现特征。

步骤:
使用 X*w代替 Xproject
使用梯度上升法
![]()

X1w1+X2w2 …上述就是点乘的问题,等价于下面的



上面的式子很好推,花三分钟就推出来了。
实现
这里使用批量梯度上升法,同理,还可以使用随机梯度上升法和小批量梯度上升法。
20-Implement-PCA-in-BGA.ipynb
前n个主成分
求出一个主成分后,当要求下一个主成分时,需要消除之前的那个主成分的影响。
下图中,蓝线是一个主成分。当求下一个主成分时,需要将样本映射到绿线上。再来求下一个主成分。
依次类推。


21-Getting-First-N-Component.ipynb
高维向低维映射
数据映射
22-Data-Projection.ipynb
scikit-learn中的PCA
23-PCA-in scikit-learn.ipynb
MNIST 7万手写体识别
PCA实现降噪
降维的时候丢失信息,其实丢失了大部分的噪音。
25-PCA-for-noice-reduction.ipynb
人脸识别和特征脸

X中的每行是一个样本,可以是一个人脸图像样本。
W中的每行,也可以理解是一个人脸,称为特征脸。每个特征脸对应一个主成分。
W中的每一行的维度是和X中的样本一样的。
特征脸:eigen face
特征值:eigen value
特征向量:eigen vector
多项式回归
简单示例

多项式回归的问题本质还是线性回归。是原有特征的组合。
上一章的PCA是降维,而这个是升维。
27-Polynomial-Regression.ipynb
scikit-learn的多项式回归和Pipeline
算是数据预处理的过程。

加上多项式回归后,数据就变得复杂了,要先处理多项式,还要归一化,再进行数据回归。所以出现了Pipeline,将这三个整合成一个。

28-Polynomial-Regression.ipynb
过拟合和欠拟合
欠拟合:

过拟合:
较好的拟合了训练样本集。
但是不能拟合测试样本集。
过多的表达了数据间的噪音关系。

29-Underfitting-and-Overfitting.ipynb
过拟合对原来的样本点能够很好的拟合,但一旦来了新的样本点,就无法进行性预测了。
模型的范化能力非常的差。
分离训练集和测试集的意义
从欠拟合到过拟合的过程。
学习曲线
随着训练样本的逐渐增多,算法训练出的模型的表现能力。
下图中横坐标表示训练样本数,纵坐标表示均方误差跟。

 31-Learning-Curve.ipynb
31-Learning-Curve.ipynb
验证数据集
面临问题:
一直用测试数据集进行评判,会出现针对特定测试数据集过拟合。例如:当通过训练数据训练好模型后,用测试数据集进行测试,一旦不理想,就换个超参数。这样一直是围绕测试数据集打转。也就是会根据测试数据集进行调参。测试数据集不应该出现在模型塑造的过程中。
解决方法:

这样又有一个问题:
验证数据集如何获取?
是随机给吗?
如果验证数据集中出现极端数据怎么办?
解决方法是交叉验证
交叉验证
![]()
交叉验证的过程中,是将各个模型的验证结果求平方,这样就避免了个别极端样本的影响
32-Validation-and-Cross-Validation.ipynb

如果有m个样本,k取m-1这种极端的情况,那么称为留一法。
留一法运行时间特别缓慢,但是能够充分反映样本的性能。有时,发表论文时会使用到。一般不会用到。

偏差和方差的权衡
偏差 : bias
方差: variance
越分散,方差越大。
越偏离,偏差越大。
偏差
方差
解决高方差(过拟合)
不使用验证集会过拟合,这是对测试数据集的过拟合。
正则化

终于理解了正则化的含义,吼吼。
出现过拟合时,theta是异常的,会出现特别大的值。

正则化就是对theta进行惩罚。
开发经验
开发经验:
岭回归是精准的,如果计算量承受的住的话,就是用岭回归。
当特征特别多(岭回归无法使θ为0,无法减少特征值),计算量承受不住,优先使用弹性网。
弹性网既有LASSO的特征选择优点,又不至于使过多的θ为0。
方式1:岭回归 ridge regression
- theta0 不需要正则化,因为theta0 是截距。
只决定曲线的高低,不形象是否过拟合。 - 取二分之一是为了求导方便
- α是一个超参数 。α为0时,等同于没有正则化,α很大时,前面的MSE就无意义了。
33-Ridge-Regression.ipynb
方式2:LASSO Regularization
比较Ridge和LASSO
Ridge会让theta变小,但不会让theta变为0。
LASSO会让部分theta变为0


在 ridge回归中,theta接近0的过程中,每个theta都不断变小,但不会为0
岭回归的三维图:


在 LASSO回归中,theta接近0的过程中,各个偏导数导数是1(或-1,反正都一样),那么在某个时刻,部分的theta会变为0,但其他的没有变为0.这就是上图中的拐点部分。
LASSO回归的三维图:
优缺点
因为LASSO会使部分的theta变为0,所以从计算的准确度而言,使用ridge较为准确。
但是当特征特别多的时候,LASSO可以让特征数变小。
开发经验:
岭回归是精准的,如果计算量承受的住的话,就是用岭回归。
当特征特别多(岭回归无法使θ为0,无法减少特征值),计算量承受不住,优先使用弹性网。
弹性网既有LASSO的特征选择优点,又不至于使过多的θ为0。
数学思想
数学相像。
L1正则,L2正则,L0正则

Lp范数是对任意一个样本的所有特征进行运算。
p=1是L1范数,等价于曼哈顿距离。
p=2是L2范数,等价于欧拉距离。
Ln正则项只是在Lp的基础上不做开p次方。
一般不用n大于3的正则项,但数学理论上存在的。

L0正则项是指使θ的个数越少,当然很少用。
实际使用L1取代,因为L0正则的优化是一个NP难的问题。使用L1(LASSO)就会使部分theta变为0,实现了L0想要达到的目的
弹性网 Elastic Net
正则项使用 是 L1正则 + L2正则。同时拥有了两者的优势。

上式中的r有时一个超参数,表示两种超参数的比例。前面的是r,后面的是1-r后面的1/2是对付平方导数的(不懂的话,拖出去打死就行)
逻辑回归
从下图可以发现,算法不是越复杂越好。
算法是越适合越好。


逻辑回归也是回归,它是在最后根据概率来判断是否。
逻辑回归本身只能解决二分类,当然,是可以处理的。
sigmod
代价函数
求导过程
sigmod(t)求导:
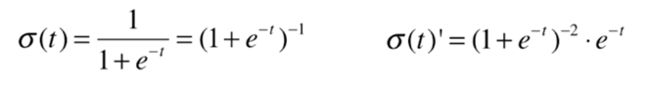
带入到log()函数进行求导:

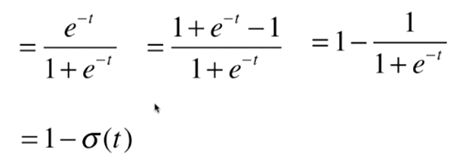
即:
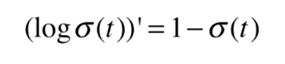
现在开始求后半部分:
先是log求导:

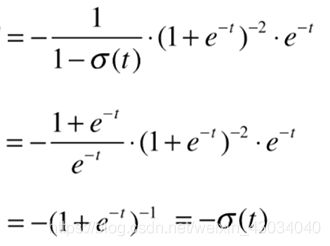
再进行整个后半部分的求导:

最后进行前后合并。


和线性回归是一样的。同样的方式进行向量化。
求导结果
逻辑回归用例
鸡尾花二分类。
先进行封装。
36-Implement-Logistic-Regression.ipynb
决策边界
逻辑回归边界
kNN决策边界
使用多项式特征
使用管道
过拟合
正则化

我们不知道样本是怎么样的,所以要使用超参数网 degree,C,penalty 都是超参数。
39-Logistic-Regression-in-sklearn.ipynb
多分类
OvA=one vs all =OvR=one vs rest

slinear_model 中的LogisticRegression
OneVsRestClassifier和OneVsOneClassifier
分类算法的评价
对于线性回归问题,评价标准有MSE、RMSE、MAE、R Square.
但是对于逻辑回归的评价标准,只有一个准确度(accuracy_score)是不够的。
问题
混淆矩阵 Confusion Matrix
精准率和召回率
前一个字母表示预测正确和错误,后一个字母表示预测值。
精准率:医生说100个人有病,其中真实有病的为36人,精准率为36%。
召回率:房间里有100个人有病,医生说有36人有病,召回率是36%
41-implement-Confusion-Matrix-Precision-and-Recall.ipynb
F1 Score
精准率和召回率的选择是视情况而定。
例如
股票选择:高精准率。选出的股票一定要涨。如果我没买的股票涨了,对我也没有损失。
医生:高召回率。有病的人来到医院一定要被检测出来。如果没病却检测出有病,只要进一步验证即可。
也可以同时兼顾这两个指指标。例如F1 Score
调和平均值比平均值要好。
平均值:一个接近0,一个接近1,平均值为0.5。
调和平均值:一个接近0,一个接近1,调和平均值接近0。这就是优点。
42-F1-Score.ipynb
Precision-Recall的平衡
精准率和召回率是相互矛盾的。很难将两个都调好

不管边界往哪里移动,精准率和召回率都会相互影响。
决策边界的修改


43-Precision-Recall-Trade-Off.ipynb

PR曲线

44-Precision-Recall-Curve.ipynb
Precision-Recall曲线
上面的PR曲线大致是下图这样。下图两条PR曲线对应2个模型。明显曲线1对应的模型较好。
![]()
ROC曲线
Receoiver Operation Characteristic Curve
描述真正例率TPR和 假正例率FPR之间的关系
TPR = 召回率
45-ROC.ipynb
多分类问题
多分类的精准率和召回率
多分类的混淆矩阵
 46-Confusion-Matrix-in-Multi-class.ipynb
46-Confusion-Matrix-in-Multi-class.ipynb
支撑向量机 SVM
由于SVM底层实现复杂,学会使用即可。
Support Vector Machine
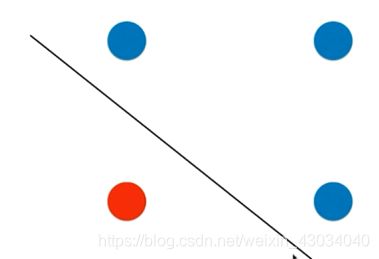
决策边界可以有很多条可以适用。

想让决策边界离红色样本越远,同时离蓝色样本也越远。

SVM思想是不仅考虑划分现有的样本,还考虑了未来的情况。
假如数据刚好是线性可分的。(当然,大部分都是不可分的,哪有一条直线刚好可以将样本分为两部分!)

线性可分:Hard Margin SVM
线性不可分: Soft Margin SVM
线性可分 Hard Margin SVM
将Wd bd重新用W b表示
线性不可分 Soft Margin SVM
错误的决策边界:

线性不可分:

从而引申出soft margin SVM:


C值越大,给的容错率越小,越接近hard margin SVM
sklearn 中的SVM
hard SVM
soft SVM
47-SVM-in-scikit-learn.ipynb
多项式
方式1:使用PolynomialFeatures增加degree

方式2:使用多项式核函数的SVM

48-Polynomial-Features-in-SVM.ipynb
核函数
之前提高阶数需要使用多项式特征添加degree。
使用核函数就是用来取代这个步骤的。交给核函数来处理。

上述推导公式不做要求。
相较于使用之前的多项式特征先变化degree,使用核函数能够降低计算量和存储空间(之前的degree上升,需要大量的存储空间)
核函数不是SVM的专属,他也是一种技巧。只不过在SVM中用的比较多。
多项式核函数
c和d就是超参数

sklearn中提供的SVC中就有kernel选择。
线性核函数
多项式核函数就是为了为线性函数添加degree.
那线性核函数就是没有degree的核函数。
高斯核函数
高斯函数属于正态分布的一种。
也叫RBF核(Radial Basis Function Kernel)、径向基函数
高斯核函数对每个样本的变形是很复杂的,变形后的结果是简单的。(就是上面的式子)
高斯核函数将每一个样本点映射到一个无穷维的特征空间。
多项式特征就是将原来线性不可分的数据线性可分。
例如:下面的线性不可分
![]()
如果把原来的转换为平方。那么久变成下面的:

这样就线性可分了。
高斯核函数做的同样也是这件事。


49-What-is-RBF-Kernel.ipynb

很容易发现,高斯是很耗计算量的。
如果初始的样本数据维度n很高,但样本数据数目m不大,那么使用高斯核函数就比较划算。例如自然语言处理。
![]()
高斯函数中,
u代表均值,
σ代表标准差,越小,图形越窄,越高。
而γ的关系和σ是呈导数的关系。
50-RBF-Kernel-in-scikit-learn.ipynb
SVM思路还可解决回归问题
和分类问题刚好相反,回归问题要求在margin里的样本点要越多越好。

epsilon 也是一个超参数。

决策树
52-What-is-Decision-Tree.ipynb
信息熵


左边的随便给你一个样本,你完全无法估计大致在哪个类里。确定性低
但右边可以确定,有很大的概率在第三个类。确定性高
53-Entropy.ipynb
使用信息熵寻找最优分化

54-Entropy-Split-Simulation.ipynb
基尼系数
两个结果值的分布对应的基尼系数值:
55-Gini-index.ipynb
两者比较
CART
Classification And Regression Tree
既可以解决回归问题,也可以解决分类问题。
![]()
生成的是二叉树。
sklearn 就是通过这种方法实现决策树的。当然还有其他,ID3,C4.5,C5.0

非常容易过拟合(所有的非参数学习都会面临过拟合问题)
剪枝需要降低复杂度,解决过拟合问题。
解决分类问题
 56-CART-and-Decision-Tree-Classifier.ipynb
56-CART-and-Decision-Tree-Classifier.ipynb
解决回归问题
思路是在分类问题的基础上取绝对值。
一个样本来到某个叶子节点,返回叶子节点中样本的平均值。
57-Decision-Tree-Regressor.ipynb
决策树的局限性
决策树并不推荐单独使用。
结合随机森林会有很好的效果。
1.只能横竖划分
2.对个别数据敏感
改变一个样本就可能改变整个模型。
58-Problem-of-Decision-Tree.ipynb
集成学习
hard voting (一人一票)
soft voting (权重)
一人一票肯定不好,专业人士应该具有的权重更大。

带有权重的预测

这要每个模型都能估计概率。
svm算法是用来搞决策边界的,但sklearn中提供求概率的函数(计算复杂,不做底层了解)

很多很多个模型
Bagging(bootstrap放)和Pasting(不放)
如果有500个样本,不放回取样的话,只能训练5个模型。放回取样可以训练很多很多个模型。
OOB (Out-of-Bag)
62-oob-和更多Bagging相关.ipynb
取出来又放回去,这样平均大概37%是没有取到的。可以直接使用这37%的样本作为测试数据集。而不需要测试和训练集分离。
简单使用
多线程运行
随机取样
随机森林
有很多的决策树模型,就形成了决策树森林。
随机森林就是集成了决策树和Bagging
63-Random-Forest-Trees-and-Extra-Trees.ipynb
随机森林
极度随机森林

使用随机的特征和阀值看起来你很扯淡,但不要忘了集成学习只需要求模型的准确度高于50%。
解决回归问题
和分类问题差不多。有空自己学习。
Boosting(增强)
同样集成多个模型。
但和Bagging不同,它的每个模型不是独立的,而是每个模型都在增强(Boosting)整体的效果。
Ada Boosting
 预测对了的样本在下一次的训练中权重会降低。
预测对了的样本在下一次的训练中权重会降低。
可以发现每个模型都在弥补上一个模型的错误。
Gradient Boosting
64-Boosting.ipynb
Stacking

思想:多个模型输出结果,再把结果作为输入创建新的一个模型(说好的建国之后不许套娃!!)
- 拆分样本,分为两份
- 将第一份样本作为训练集,训练上面的三个模型
- 将第二份样本作为测试集,每个样本得到三个预测值
- 将第二份样本和对应的预测值组合成新的样本,投入到新的模型训练中。
sklearn文档的使用
user guide
user guide相当于一本机器学习的书,有兴趣可以通读
user guide的每一部分先是介绍,点击着重字体会进入到API的具体使用。
API
API是每个可以使用的函数。也就是我们用到的东西。
进入API后可以使用网页查找找到具体的内容