Java实现冒泡排序、快速排序算法

一、排序算法

1.1 概念

排序：假设含有n个记录的序列为{R1，R2，…,Rn},其相应的关键字序列为{K1，K2，…,Kn}。将这些记录重新排序为{Ri1,Ri2,…,Rin},使得相应的关键字值满足条Ki1<=Ki2<=…<=Kin,这样的一种操作称为排序。
通常来说，排序的目的是快速查找。

1.2 排序衡量标准

衡量排序算法的优劣：
1.时间复杂度：分析关键字的比较次数和记录的移动次数
2.空间复杂度：分析排序算法中需要多少辅助内存
3.稳定性：若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种排序算法是稳定的。

1.3 排序的分类

排序算法分类：内部排序和外部排序。
内部排序：整个排序过程不需要借助于外部存储器（如磁盘等），所有排序操作都在内存中完成。
==说明：==后面详细讲的冒泡排序、快速排序、归并排序和堆排序都是内部排序。
外部排序：参与排序的数据非常多，数据量非常大，计算机无法把整个排序过程放在内存中完成，必须借助于外部存储器（如磁盘）。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。

二、冒泡排序

排序思想：
相邻两元素进行比较，如有需要则进行交换，每完成一次循环就将最大元素排在最后（如从小到大排序），下一次循环是将其它的数进行类似操作。
效率分析：
时间效率：O（n^2）
空间效率：空间效率很高，只需要一个附加程序单元用于交换，其空间效率为O(1)
稳定性：稳定
实现代码如下：

public class SortTest {
     
 public static void main(String[] args) {
     
  int[] arr = new int[] {
     23,445,32,65,-32,-43,0,9,72,32};
  //使用冒泡排序实现数组元素从小到大的顺序排序
  for(int i = 0;i < arr.length -1;i++) {
     
   for(int j = 0;j < arr.length-1-i;j++) {
     
   if(arr[j] > arr[j+1]) {
     
    int temp = arr[j];
    arr[j] = arr[j+1];
    arr[j+1] = temp;
   }
  }
 } for(int i = 0; i< arr.length;i++) {
     
  System.out.print(arr[i] + "  ");}
 }
}

三、快速排序

在java.util包下的Arrays类sort()方法：用来对array进行排序。底层使用快速排序。
快排思路：
快速排序也是交换排序的一种。
其核心思想是分治法。步骤：
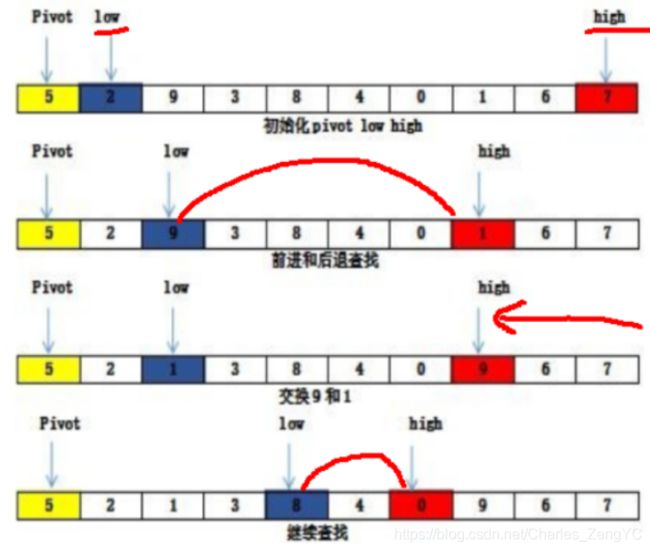
1.设立一个基准数，如下图所示，第一个数5为基准数。
2.设置两个指针low和high，指向数列的最左和最右两个元素，如图low索引对应的数据为2，high索引对应的数据为7.
3.low从左向右移动，找到比基准数大的值停止；high从右往左移动，找到比基准数小的值停止；第一次low对应数据为9，high对应数据为1时为第一次满足情况。
4.交换这low和high索引对应的值；
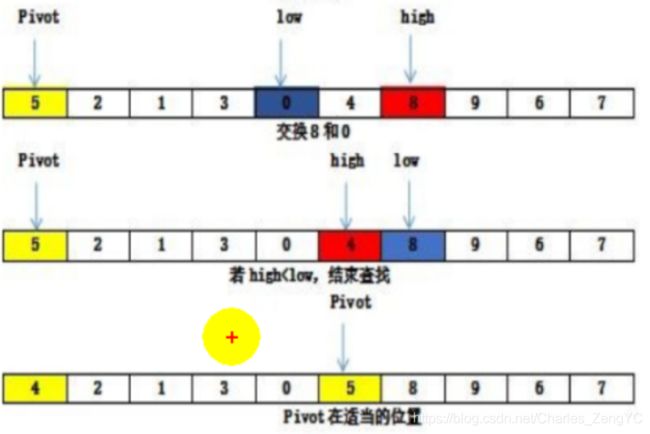
5.继续第三步，low和high指针继续移动。直到low的索引大于high索引时停止。
6.把基准值放到合适的索引位置。如图基准值5跟4位置交换。即把基准值的索引与最后一次high索引交换。
7.再次重复以上步骤

效率分析：
算法的时间效率：在分治法的思想下，原数列在每一轮被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止。故时间复杂度为O(nlogn)
算法的空间效率：由于使用递归，而递归使用栈，因此空间效率最优时为O(logn)
算法的稳定性：由于包含跳跃式交换，因此不稳定

（1）swap交换两个数的静态方法

 private static void swap(int[] data, int i, int j) {
     
  int temp = data[i];
  data[i] = data[j];
  data[j] = temp;
 }
 

（2）快速排序核心代码

private static void subSort(int[] data, int start, int end) {
     
  if (start < end) {
     
   int base = data[start];
   int i = start;
   int j = end + 1;
   while (true) {
     
    while (i < end && data[++i] - base <= 0)//从左往右首次直到比base大的数
     ;
    while (j > start && data[--j] - base >= 0)//从右往左直到出现比base小的数
     ;
     if (i < j) {
     
     swap(data, i, j);//交换两个数，其实可以理解为把这两个索引交换
    } else {
     
     break;
    }
 }
   swap(data, start, j);//把基准值换到合适的位置。其实就是最后一次的high索引所对应位置
   subSort(data, start, j - 1);//递归调用
   subSort(data, j + 1, end);
    }
 }
public static void quickSort(int[] data){
     
  subSort(data,0,data.length-1);
 }

（3）主方法（测试）

public static void main(String[] args) {
     
  int[] data = {
      9, -16, 21, 23, -30, -49, 21, 30, 30 };
  System.out.println("排序之前：\n" + Arrays.toString(data));
  quickSort(data);
  System.out.println("排序之后：\n" + java.util.Arrays.toString(data));
 }

四、了解堆排序和归并排序

4.1 堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。
堆排序是将数据看成是完全二叉树、根据完全二叉树的特性来进行排序的一种算法，那么：
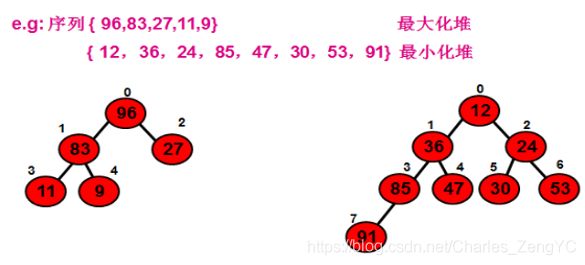
1.最大堆要求节点的元素都要不小于其孩子，最小堆要求节点元素都不大于其左右孩子
2.那么处于最大堆的根节点的元素一定是这个堆中的最大值

说明：
完全二叉树： 除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐。
满二叉树：除了叶子结点之外的每一个结点都有两个孩子，每一层(当然包含最后一层)都被完全填充。

4.2 归并排序

二路归并排序的基本思想：将两个有序表合并成一个有序表。
例如，将下列两个已排序的顺序表合并成一个已排序表。顺序比较两者的相应元素，小者移入另一表中，反复如此，直至其中任一表都移入另一表为止。

如图一：13与7比较，7更小，把7放入

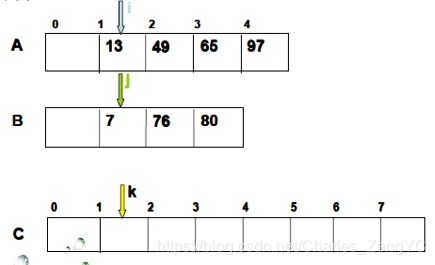
如图二：13与76比较，13更小，把13放入

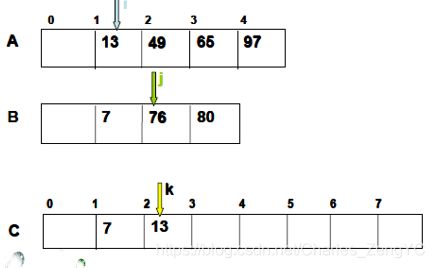
如图三：继续比较下去，至B表元素都已移入C表，只需将A表的剩余部分移入C即可。

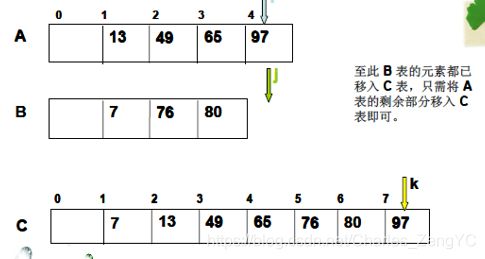
2-路归并排序的具体过程范例如下：

算法的时间效率：归并算法需要递归地进行分解、合并，每进行一趟归并排序，需要merge()方法一次，每次执行merge()需要比较n次，故复杂度为O(n*logn)
算法的空间效率：较差，需要一个与原始序列同样大小的辅助序列
算法的稳定性：稳定