Matlab吴恩达机器学习编程练习ex4:神经网络Neural Networks Learning
本文基于吴恩达老师第五周的练习,在这次的练习中,你将会实现神经网路的后向传播算法(BP神经网络)。
作业大纲
- 1 神经网络 Neural Networks ex4.m
-
- 1.1 数据可视化
- 1.2 模型表示
- 1.3 前向传播和代价函数 nnCostFunction.m
- 1.4 正则化代价函数
- 2 后向传播 nnCostFunction.m
-
- 2.1 Sigmoid函数的导数 sigmoidGradient.m
- 2.2 随机初始化 randInitializeWeights.m
- 2.3 后向传播
- 梯度检查
- 2.5 正则化神经网络
- 2.6 使用fmincg来学习参数
- 3 隐层可视化
- 总结
1 神经网络 Neural Networks ex4.m
在以前的练习中,你实现了神经网络的前向传播并且用已知的权重进行手写数字的预测。在这次的练习中,你将实现后向传播算法进行参数的学习。
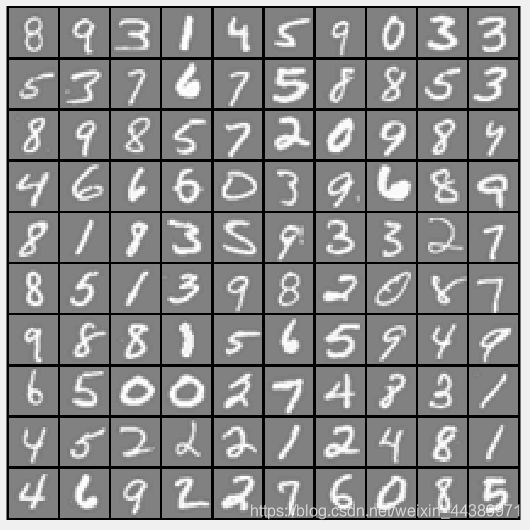
1.1 数据可视化
就和上周一样展示数据,有5000个样本,一个样本就是一张手写数字的图片,20*20px,有400个特征。然后y中,0用10来表示,其他数字不变。
1.2 模型表示
本次训练的模型是一个三层的神经网络,一个输入层,有400个单元。一个隐含层,有25个单元。一个输出层,有十个单元,分别对应了十个数字类别。
1.3 前向传播和代价函数 nnCostFunction.m
现在你将要实现神经网络的代价函数以及梯度。首先,完成nnCostFunction.m这个函数的代码去返回cost的值。回忆一下没有正则化的神经网络的代价函数公式:
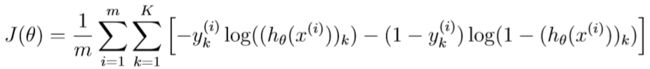
在完成了上述的公式代码之后,你可以在屏幕上看见代价为0.287629,下面是这部分的代码
a1 = [ones(m, 1) X]; %5000x401
z2 = a1 * Theta1'; %5000x25 Theta1 25*401
a2 = sigmoid(z2); %5000x25
a2 = [ones(m, 1) a2]; %5000x26
z3 = a2 * Theta2'; %5000x10 Theta2 10×26
a3 = sigmoid(z3); %5000x10
h = a3; %5000x10
u = eye(num_labels);
y = u(y,:);
J = 1/m*(sum(sum(-y .* log(h) - (1 - y) .* log(1 - h))));
1.4 正则化代价函数
公式如下:
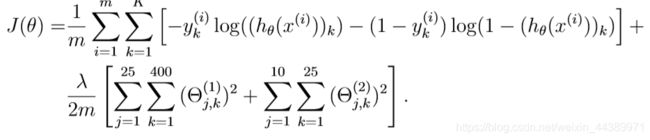
这就是在上面的基础上再加上正则项目,但是要注意这个正则项是从1开始计算的。
修改这部分代码即可:
regularization = lambda/(2 * m) * (sum(sum(Theta1(:,2:end) .^ 2)) + sum(sum(Theta2(:,2:end) .^ 2)));
J = J + regularization;
这时候的cost就变成了0.383770.
2 后向传播 nnCostFunction.m
在这部分的练习中,你将会用后向传播算法计算神经网络代价函数的梯度。你需要继续完成nnCostFunction.m使得这个函数返回一个合适的梯度值。
2.1 Sigmoid函数的导数 sigmoidGradient.m
为了帮助你开始这个部分的练习,你将要最先实现sigmoid梯度函数,如下:
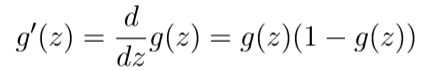
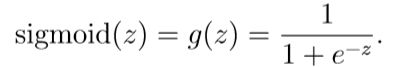
根据上述公式完成sigmoidGradient.m函数,当你完成了,你可以通过调用函数来进行验证,当z的值都很大时,不管正负,结果应该是接近于0的,当z=0,其值应为0.25。你的公式不仅要适用于一个数字,对于向量矩阵都能计算出每一个元素的值。
function g = sigmoidGradient(z)
%SIGMOIDGRADIENT returns the gradient of the sigmoid function
%evaluated at z
% g = SIGMOIDGRADIENT(z) computes the gradient of the sigmoid function
% evaluated at z. This should work regardless if z is a matrix or a
% vector. In particular, if z is a vector or matrix, you should return
% the gradient for each element.
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the gradient of the sigmoid function evaluated at
% each value of z (z can be a matrix, vector or scalar).
s = 1.0 ./ (1.0 + exp(-z));
g = s .* (1-s);
% =============================================================
end
2.2 随机初始化 randInitializeWeights.m
当训练神经网络时,随机的初始化参数来防止对称现象的发生。一个有效的随机初始化的方法是,随机地在[−ε init,init]初始化Θ的值。代码如下:
function W = randInitializeWeights(L_in, L_out)
W = zeros(L_out, 1 + L_in);
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init;
end
2.3 后向传播
给出训练样本,我们想要实现前向传播去计算所有的在这个神经网络里面的激活单元,包括输出层的假设函数值。然后,对于每一个l的每一个结点,我们要计算偏差项δ。
对于输出结点,我们会直接计算不同的神经网络激活单元和正确的目标值。而对于隐藏层,你将通过第l+1层的节点偏差项的权重平均值计算![]() 。
。
更详细的,下面是实现后向传播的算法。你需要实现步骤1-4在一个循坏里面,一次处理一个样本。具体来说,你需要实现for循坏,用for i = 1:m然后讲步骤1-4放在这个循环里面,那么第i次迭代就是计算第i个样本。然后第五步会将所有的梯度值相加在除m,获得了神经网络的代价函数的梯度。
- 将第输入层的值设置成第t个训练样本。先进行前向传播,计算出第2层和第3层的激活单元值。
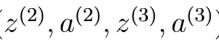
在第2层和第3层添加偏置单元。a 1 = [1 ; a 1] - 对于每一个输出单元k,设置:
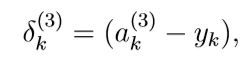
这里的yk是0,1变量,就是说当属于这类是就是1,其他的就是0.
3.对于第2层,设置
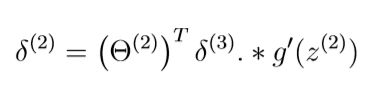
4.将梯度值相加。
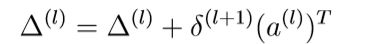
5.将梯度值/m。
代码如下:
delta3 = a3 - y; % 5000 * 10
delta2 = delta3 * Theta2; % 5000 * 26
delta2 = delta2(:,2:end); % 5000 * 25
delta2 = delta2 .* sigmoidGradient(z2); % 5000 * 25
Delta1 = zeros(size(Theta1)); % 25 * 401
Delta2 = zeros(size(Theta2)); % 10 * 26
Delta1 = Delta1 + delta2' * a1; % 25 * 401 5000×25' * 5000x401
Delta2 = Delta2 + delta3' * a2; % 10 * 26 5000×10' * 5000x26
梯度检查
在你的神经网络中,你在最小化代价函数J。为了进行梯度检查,你可以想象展开系数Θ1和Θ2,变成一个长向量θ。通过这样做,你可以认为下面的梯度检查过程来代替代价函数。
假设你有一个函数,并且你想要算偏导数,并且你想要检车所得到的结果是不是正确。
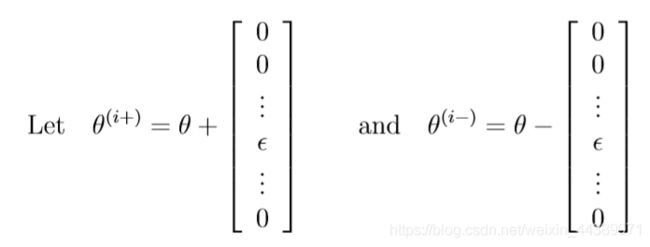
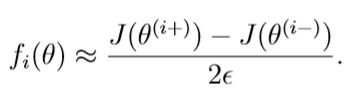
这两个值彼此近似的程度取决于J的细节。但是,假设= 10−4,通常会发现上述内容的左边和右边至少要4个有效数字(并且通常还要更多)。在这个部分代码已经写好了,你需要看一看并理解他是怎么样运行的。如果说你的代码正确的话,你将会看到相关误差小于1e-9.
2.5 正则化神经网络
在你成功的完成后向传播算法后,你将要加入正则项。结果表明你可以用后向传播计算完梯度后,再将正则项加进去。公式如下:
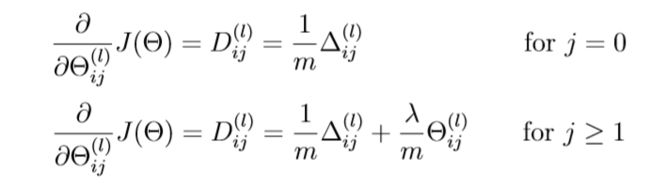
要记住偏置单元是不需要被正则的。
2.6 使用fmincg来学习参数
当你成功的完成了上述的步骤之后,下一步是使用fmincg函数去优化参数。完成训练之后,ex.m脚本会向你报告你分类的准确率。如果说你的程序是正确的话,你就会看见95.3%的正确率(这个可能会有1%的变化因为随机初始化参数的不同)。也会随着迭代的增多,正确率会变高。我们建议你去尝试更多迭代次数的神经网络,比如400次等等,也可以尝试改变正则化系数λ。通过正确的学习设置,让神经网络完美的拟合训练集是很有可能的。
3 隐层可视化
一种理解你的神经网络的方法是学习可视化隐层神经元所代表的。通俗一点,给出一个特殊的隐层单元,将他所计算的东西可视化的一个方法是找一个能激活他的输入x。
总结
对于神经网络这节,是比较抽象难理解的一个章节。包括做题目的时候按照老师说的新手用循坏来做。发现其实还是矩阵来做更加清晰。当然,对于这些章节还是需要再反复斟酌的。对于这篇文章还是比较乱,在我的草稿箱里存了好久,仅供参考!下面是我的成绩: