红黑树的插入、及模拟实现红黑树(附代码 + 图解 + 注释)
1.红黑树概念及性质
红黑树:为一棵二叉搜索树,树中的每一个结点颜色不是红色就是黑色。
红黑树性质:
- 根节点和所有的外部节点的颜色都是黑色;外部节点为叶子节点的左右孩子节点
- 从根节点到外部节点的途中没有连续两个节点的颜色为红色;
- 从根节点到外部节点的所有路径上都有着相同的黑色节点。
- 最长路径中节点个数不会超过最短路径节点个数的两倍。
证第4条性质:
假设一红黑树任意路径的黑色节点个数为r,由性质2可得,不存在连续两个红色的节点,因此红色节点 后面都会跟随着黑色节点,则从根节点到任一外部节点路径上都有r~2r个节点。故得证。
结论1.设h为红黑树的高度,n为树中节点的个数,r为任一路径的黑色节点个数,则有以下关系:
(1) h ≤ 2r
(2) n ≥ 2^r - 1
(3) h ≤ 2log2(n + 1)
证明:
(1)从根到任一外部节点的路径长度不超过2r,同时从树的定义可知,树的高度即为根节点的高度,等于从根到离根最远的外部节点的路径的长度,因此有h ≤ 2r。
(2)红黑树任一路径黑色节点数为r,则从第1层到第r层没有外部节点,因而在这些层内共有2^r - 1个内部节点,也就是说,内部节点的总数至少为2 ^ r - 1。
(3)由(2)得 r ≤ log2(n + 1),则推得,h ≤ 2log2(n + 1)。
红黑树的最大高度为2log2(n + 1),所以插入、搜索、删除的时间复杂度为O(log2(n))。
2.红黑树的插入
使用bst的插入算法将一个元素插入到红黑树中,将该元素作为新的叶节点插入到某一位置,并为该元素进行染色。
- 如果插入前为空树,那么新元素将成为根节点,根据性质1,根节点必须为黑色;
- 如果插入前树非空,若新节点被染成黑色,那么将违反性质3,根节点到任一外部节点路径上黑色节点数不相等,因此,一般将新插入的节点默认为染成红色,但这可能会违反性质2,出现连续2个红色节点,故需要重新平衡。
cur:当前节点,parent:父节点,grandfather:祖父节点,uncle:叔叔节点
2.1 第一种情况
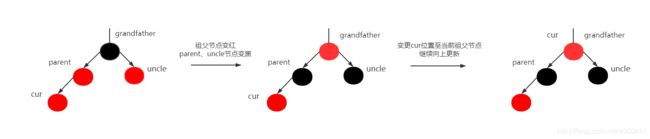
cur为红,parent为红,grandfather为黑,uncle存在且为红。
cur 和 parent 出现连续两个红色节点,则违反了性质3,解决办法:对parent、uncle节点染色为黑,将grandfather染色为红色,此时可能依然会出现两个连续的红色节点,则将cur节点变更为grandfather节点,继续向上更新。
情况1伪代码:
if (uncle && uncle->_color == RED)//uncle节点存在且为红色
{
parent->_color = BLACK;//父节点变为黑色
uncle->_color == BLACK;//叔叔节点变为黑色
grandfather->_color = RED;//祖父节点变为红色
cur = grandfather;//cur变更为当前祖父节点,继续向上更新
parent = cur->_parent;//parent变为当前cur的父节点
}
继续向上更新是因为,当前祖父节点可能是子树,可能为根节点,若为子树,则需要向上更新,若为根节点,则在更新完毕之后,再将根节点置为黑色。
2.2 第二种情况
cur为红,parent为红,grandfather为黑,uncle不存在或者uncle为黑。
uncle的两种情况:
- 如果uncle节点不存在,则cur一定为刚插入的新节点,因为如果cur不是新插入的节点,则cur和parent一定有一个节点的颜色为黑色,则不满足性质3,每条路径上黑色节点数相同;
- 如果uncle节点存在,则一定为黑色,那么cur节点原来的颜色一定是黑色的,现在变为红色是因为cur的子树在调整的过程中将cur节点的颜色由黑色变为了红色。
解决办法:parent为grandfather的左孩子,cur为parent的左孩子,对grandfather进行右单旋,parent变为黑色,grandfather变为红色。
2.3 第三种情况
cur为红,parent为红,grandfather为黑,uncle不存在或者uncle为黑。
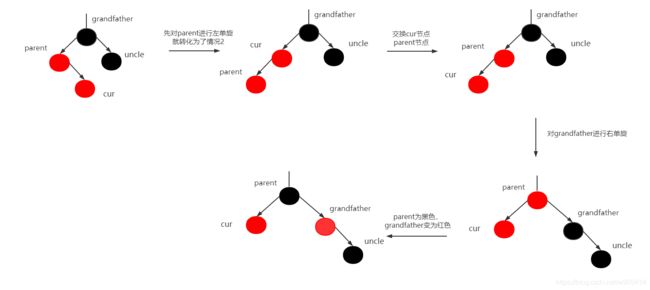
这种情况下,主要是cur节点在parent节点右侧。
解决办法:parent为grandfather的左孩子,cur为parent的右孩子,先对parent进行左单旋,交换cur和parent节点,再对grandfather进行右单旋,parent变为黑色,grandfather变为红色。
情况2与情况3伪代码:
if (cur == parent->_right)//cur节点在右侧,先左单旋,转化为情况2
{
RotateLeft(parent);//左单旋
swap(parent, cur);//交换parent和cur节点
}
RotateRight(grandfather);//祖父节点右单旋
grandfather->_color = RED;//祖父颜色变为红色
parent->_color = BLACK;//父节点颜色变为黑色
上述三种情况,全部是在parent节点在祖父节点左侧的情况。
下面讨论,parent节点在祖父节点右侧的情况。
2.4 第四种情况
cur为红,parent为红,grandfather为黑,uncle存在且为红。
与情况一类似,解决方法相同。
解决办法:对parent、uncle节点染色为黑,将grandfather染色为红色,此时可能依然会出现两个连续的红色节点,则将cur节点变更为grandfather节点,继续向上更新。
情况4伪代码:
if (uncle && uncle->_color == RED)//uncle节点存在且为红色
{
parent->_color = BLACK;//父节点变为黑色
uncle->_color == BLACK;//叔叔节点变为黑色
grandfather->_color = RED;//祖父节点变为红色
cur = grandfather;//cur变更为当前祖父节点,继续向上更新
parent = cur->_parent;//parent变为当前cur的父节点
}
2.5 第五种情况
cur为红,parent为红,grandfather为黑,uncle不存在或者uncle为黑。
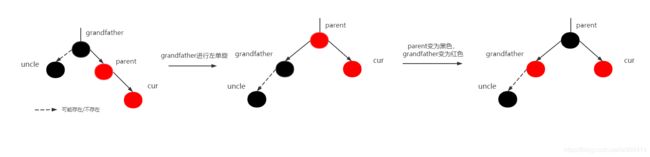
cur为parent的右孩子。
解决办法:parent为grandfather的右孩子,cur为parent的右孩子,对grandfather进行左单旋,parent变为黑色,grandfather变为红色。
2.6 第六种情况
cur为红,parent为红,grandfather为黑,uncle不存在或者uncle为黑。
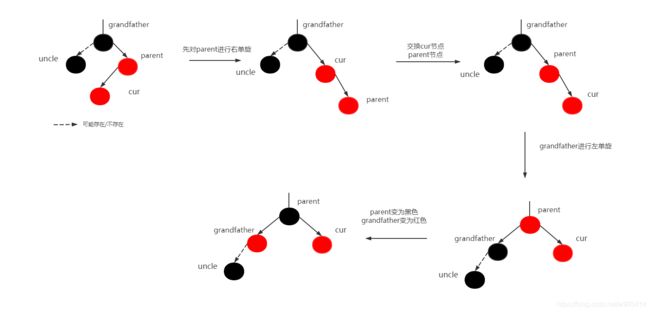
cur为parent的左孩子。
解决办法:parent为grandfather的右孩子,cur为parent的左孩子,先对parent进行右单旋,交换cur和parent节点,再对grandfather进行左单旋,parent变为黑色,grandfather变为红色。
情况5与情况6伪代码:
if (cur == parent->_left)//cur节点在左侧,先右单旋,转化为情况5
{
RotateRight(parent);//左单旋
swap(parent, cur);//交换parent和cur节点
}
RotateLeft(grandfather);//祖父节点右单旋
grandfather->_color = RED;//祖父颜色变为红色
parent->_color = BLACK;//父节点颜色变为黑色
3.模拟实现红黑树
#pragma once
#include