AVL树的四种旋转,模拟实现AVL树
AVL树又称高度平衡的二叉搜索树,引入AVL树是为了提高二叉搜索树的查找效率,减小树的平均搜索长度,因此,每向二叉搜索树插入一个新节点时就必须调整树的结构,使得二叉搜索树保持平衡,从而降低树的高度,减少树的平均搜索长度。 -------殷人昆《数据结构》
目录
- 1.AVL树的性质
- 2. 单旋转
-
- 2.1左单旋
- 2.2右单旋
- 3.双旋转
-
- 3.1右左双旋
- 3.2左右双旋
- 4. 如何选择哪一种旋转?
- 5.模拟实现
1.AVL树的性质
- 一颗空树是AVL树;
- 左右子树的高度之差绝对值不超过1;
- 任一节点的平衡因子只能取-1,0,1;(平衡因子 = 右子树高度 - 左子树高度 或者 左子树高度 - 右子树高度)
如果在一颗原本是平衡的二叉搜索树中插入一个新节点,可能就会造成不平衡,因此必须调整树的结构,使树平衡化。 旋转分为两种:单旋转(左单旋、右单旋),双旋转(右左双旋、左右双旋)。
以下旋转中:平衡因子 = 右子树高度 - 左子树高度
2. 单旋转
2.1左单旋
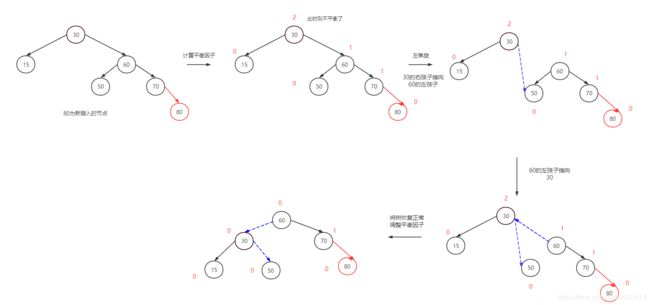
左单旋:新插入的节点在较高右子树的右侧:右右。
图解:
左单旋中的步骤:
- 找到当前不平衡的节点
- 让其右子树成为其父亲节点
- 该右子树的左分支节点作为当前不平衡节点的右分支
- 注意:①当前不平衡节点不为根节点时,需要注意;②当前右子树其左分支节点为空时。
具体实现可看代码代码:
void RotateLeft(Node* parent)//左单旋
{
Node* subR = parent->_right;//右孩子
if (subR->_left != nullptr)//右孩子的左分支不为空
subR->_left->_parent = parent;//改变其父节点指向
parent->_right = subR->_left;//parent的右孩子,节点变化
subR->_left = parent;//其subR的左分支节点为当前parent节点
subR->_parent = parent->_parent;//subR的父节点为parent的父节点
if (parent->_parent == nullptr)//说明parent为根节点,左单旋后,需要更改根节点位置
{
_root = subR;
}
else //说明parent不为根节点,需要判断是其右子树还是左子树
{
if (parent == parent->_parent->_left)
parent->_parent->_left = subR;
else
parent->_parent->_right = subR;
}
parent->_parent = subR;//改变当前parent父节点的指向
parent->_bf = subR->_bf = 0;//调整好了,平衡因子,置为0
}
2.2右单旋
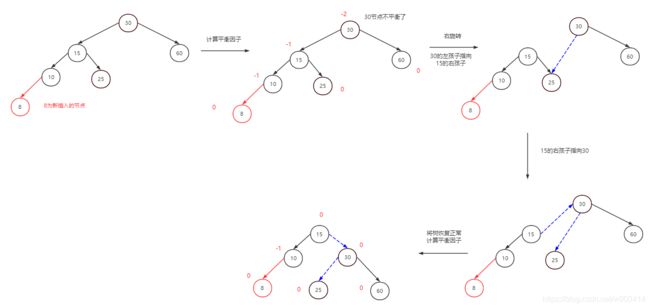
右单旋:新插入的节点在较高左子树的左侧:左左。
图解:
- 找到当前不平衡的节点
- 让其左子树成为其父节点
- 让该左子树的右分支作为当前不平衡节点的左分支
- 需要注意:①当前不平衡节点不为根节点时;②当前左子树其右分支节点为空时。
具体实现可看代码代码:
void RotateRight(Node* parent)//右单旋
{
Node* subL = parent->_left;//左孩子
if (subL->_right != nullptr)//左孩子的右分支不为空
subL->_right->_parent = parent;//改变其父节点指向
parent->_left = subL->_right;//parent的左孩子,节点变化
subL->_right = parent;//其subL的右分支节点为当前parent节点
subL->_parent = parent->_parent;//subL的父节点为parent的父节点
if (parent->_parent == nullptr)//说明parent为根节点,左单旋后,需要更改根节点位置
{
_root = subL;
}
else //说明parent不为根节点,需要判断是其右子树还是左子树
{
if (parent == parent->_parent->_left)
parent->_parent->_left = subL;
else
parent->_parent->_right = subL;
}
parent->_parent = subL;//改变当前parent父节点的指向
parent->_bf = subL->_bf = 0;//调整好了,平衡因子,置为0
}
3.双旋转
3.1右左双旋
右左双旋:新插入的节点在较高右子树的左侧插入:右左
图解:
右左单旋中的步骤:
- 找到当前不平衡的节点
- 先对其进行右旋转,可看出,此时树就变成了,在较高右子树的右侧插入
- 再进行左旋转,即可得到AVL树
具体实现可看代码代码:
void RotateRL(Node* parent)// 右左双旋
{
RotateRight(parent->_right);
RotateLeft(parent);
}
3.2左右双旋
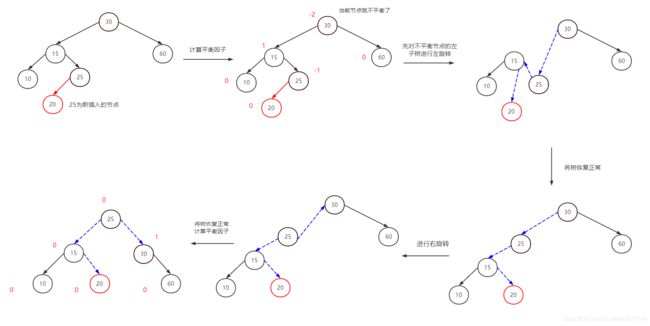
左右双旋:新插入的节点在较高左子树的右侧插入:左右
图解:
- 找到当前不平衡的节点
- 先对其进行左旋转,可看出,此时树就变成了,在较高左子树的左侧插入
- 再进行右旋转,即可得到AVL树
具体实现可看代码代码:
void RotateLR(Node* parent)// 左右双旋
{
RotateLeft(parent->_left);
RotateRight(parent);
}
4. 如何选择哪一种旋转?
根据平衡因子去看,这里我是用右子树高度 - 左子树高度
- 当前父节点不平衡,父节点平衡因子为 2,当前子节点平衡因子与父节点平衡因子同号,右右插入,选择左单旋
- 当前父节点不平衡,父节点平衡因子为 2,当前子节点平衡因子与父节点平衡因子异号,右左插入,选择右左双旋
- 当前父节点不平衡,父节点平衡因子为 -2,当前子节点平衡因子与父节点平衡因子同号,左左插入,选择右单旋
- 当前父节点不平衡,父节点平衡因子为 -2,当前子节点平衡因子与父节点平衡因子异号,左右插入,选择左右双旋
| 父节点平衡因子 | 当前节点平衡因子 | 符号状态 | |
|---|---|---|---|
| 右单旋 | 小于-1 | 等于-1 | 同号 |
| 左单旋 | 大于1 | 等于1 | 同号 |
| 左右双旋 | 小于-1 | 等于1 | 异号 |
| 右左双旋 | 大于1 | 等于-1 | 异号 |
还是不清楚的小伙伴,可以结合上面的图解,每一张图的第二个平衡因子图。有问题可以评论区或者私我哦
5.模拟实现
完整代码:
#pragma once
using namespace std;
template<class T>
struct AVLTreeNode
{
AVLTreeNode(const T& x = T())
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(x)
,_bf(0)
{
}
AVLTreeNode<T>* _left;
AVLTreeNode<T>* _right;
AVLTreeNode<T>* _parent;
T _data;
int _bf;//平衡因子
};
template<class T>
class AVLTree
{
typedef AVLTreeNode<T> Node;
public:
AVLTree()
:_root(nullptr)
{
}
~AVLTree()
{
//Destroy(_root);
}
bool Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
return true;
}
// 根节点不是空节点,则需要对插入的节点,进行调整
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (data < cur->_data)
cur = cur->_left;
else if (data > cur->_data)
cur = cur->_right;
else//不插入重复的元素
return false;
}
//插入新节点
cur = new Node(data);
if (parent->_data > data)
parent->_left = cur;
else
parent->_right = cur;
cur->_parent = parent;
//插入新节点之后,该双亲节点的平衡性会遭到破坏
// 这里我计算的平衡因子为:用右子树高度减去左子树高度
while (parent)
{
if (cur == parent->_left)//左子树高度增加
--parent->_bf;
else
++parent->_bf;
if (parent->_bf == 0)//此时为平衡的,则不需要调整
break;
else if (parent->_bf == 1 || parent->_bf == -1)//当前的子树,是平衡的,但是破坏了整体的AVL树平衡性
{
//树不平衡,则需要向上更新,调整AVL树
cur = parent;
parent = parent->_parent;
}
else
{
//parent平衡因子为2 或者 -2,则需要对AVL树进行旋转处理
if (parent->_bf == 2)
{
if (cur->_bf == 1)//右右,左单旋
RotateLeft(parent);
else // 右左
RotateRL(parent);
}
else
{
if (cur->_bf == -1)//左左,右单旋
RotateRight(parent);
else // 左右
RotateLR(parent);
}
break;
}
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalanceTree()
{
if (_root == nullptr)
return true;
bool flag = true;
_IsBalanceTree(_root, flag);
return flag;
}
private:
bool _IsBalanceTree(Node* root, bool& flag)
{
if (root == nullptr)
return 0;
int right = _IsBalanceTree(root->_right, flag) + 1;
int left = _IsBalanceTree(root->_right, flag) + 1;
if (abs(right - left) > 1)
flag = false;
return right > left ? right : left;
}
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}
void RotateLeft(Node* parent)//左单旋
{
Node* subR = parent->_right;//右孩子
if (subR->_left != nullptr)//右孩子的左分支不为空
subR->_left->_parent = parent;//改变其父节点指向
parent->_right = subR->_left;//parent的右孩子,节点变化
subR->_left = parent;//其subR的左分支节点为当前parent节点
subR->_parent = parent->_parent;//subR的父节点为parent的父节点
if (parent->_parent == nullptr)//说明parent为根节点,左单旋后,需要更改根节点位置
{
_root = subR;
}
else //说明parent不为根节点,需要判断是其右子树还是左子树
{
if (parent == parent->_parent->_left)
parent->_parent->_left = subR;
else
parent->_parent->_right = subR;
}
parent->_parent = subR;//改变当前parent父节点的指向
parent->_bf = subR->_bf = 0;
}
void RotateRight(Node* parent)//右单旋
{
Node* subL = parent->_left;//左孩子
if (subL->_right != nullptr)//左孩子的右分支不为空
subL->_right->_parent = parent;//改变其父节点指向
parent->_left = subL->_right;//parent的左孩子,节点变化
subL->_right = parent;//其subL的右分支节点为当前parent节点
subL->_parent = parent->_parent;//subL的父节点为parent的父节点
if (parent->_parent == nullptr)//说明parent为根节点,左单旋后,需要更改根节点位置
{
_root = subL;
}
else //说明parent不为根节点,需要判断是其右子树还是左子树
{
if (parent == parent->_parent->_left)
parent->_parent->_left = subL;
else
parent->_parent->_right = subL;
}
parent->_parent = subL;//改变当前parent父节点的指向
parent->_bf = subL->_bf = 0;
}
void RotateRL(Node* parent)// 右左双旋
{
RotateRight(parent->_right);
RotateLeft(parent);
}
void RotateLR(Node* parent)// 左右双旋
{
RotateLeft(parent->_left);
RotateRight(parent);
}
private:
Node* _root;
};