【啃书】《智能优化算法及其MATLAB实例》例5.1蚁群算法求解TSP问题

问题描述

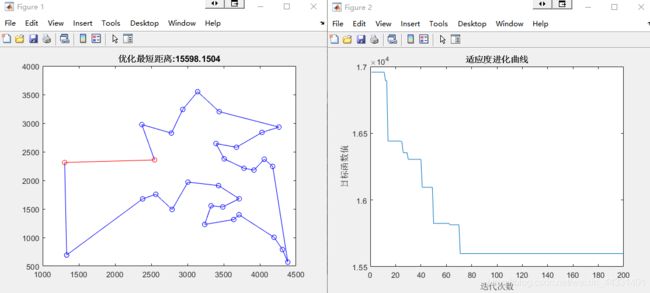
仿真过程

matlab源码

%20201012lu注：该matlab代码成功在matlabR2019a运行
%%%%%%%%%%%%%%%%%%%%蚁群算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;                %清除所有变量
close all;                %清图
clc;                      %清屏
m=50;                     %蚂蚁个数
Alpha=1;                  %信息素重要程度参数              
Beta=5;                   %启发式因子重要程度参数
Rho=0.1;                  %信息素蒸发系数
G_max=200;                %最大迭代次数
Q=100;                    %信息素增加强度系数
% C=[6734	1453
% 2233	10
% 5530	1424
% 401	841
% 3082	1644
% 7608	4458
% 7573	3716
% 7265	1268
% 6898	1885
% 1112	2049
% 5468	2606
% 5989	2873
% 4706	2674
% 4612	2035
% 6347	2683
% 6107	669
% 7611	5184
% 7462	3590
% 7732	4723
% 5900	3561
% 4483	3369
% 6101	1110
% 5199	2182
% 1633	2809
% 4307	2322
% 675	1006
% 7555	4819
% 7541	3981
% 3177	756
% 7352	4506
% 7545	2801
% 3245	3305
% 6426	3173
% 4608	1198
% 23	2216
% 7248	3779
% 7762	4595
% 7392	2244
% 3484	2829
% 6271	2135
% 4985	140
% 1916	1569
% 7280	4899
% 7509	3239
% 10	2676
% 6807	2993
% 5185	3258
% 3023	1942];                %31个省会城市坐标

C=[1304 2312
    3639 1315
    4177 2244
    3712 1399
    3488 1535
    3326 1556
    3238 1229
    4196 1004
    4312 790
    4386 570
    3007 1970
    2562 1756
    2788 1491
    2381 1676
    1332 695
    3715 1678
    3918 2179
    4061 2370
    3780 2212
    3676 2578
    4029 2838
    4263 2931
    3429 1908
    3507 2376
    3394 2643
    3439 3201
    2935 3240
    3140 3550
    2545 2357
    2778 2826
    2370 2975];

%%%%%%%%%%%%%%%%%%%%%%%%第一步：变量初始化%%%%%%%%%%%%%%%%%%%%%%%%
n=size(C,1);              %n表示问题的规模（城市个数）
D=zeros(n,n);             %D表示两个城市距离间隔矩阵
for i=1:n
    for j=1:n
        if i~=j
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j)=eps;
        end
        D(j,i)=D(i,j);
    end
end
Eta=1./D;                    %Eta为启发因子，这里设为距离的倒数
Tau=ones(n,n);               %Tau为信息素矩阵
Tabu=zeros(m,n);             %存储并记录路径的生成
NC=1;                        %迭代计数器
R_best=zeros(G_max,n);       %各代最佳路线
L_best=inf.*ones(G_max,1);   %各代最佳路线的长度
figure(1);%优化解
while NC<=G_max            
    %%%%%%%%%%%%%%%%%%第二步：将m只蚂蚁放到n个城市上%%%%%%%%%%%%%%%%
    Randpos=[];
    for i=1:(ceil(m/n))
        Randpos=[Randpos,randperm(n)];
    end
    Tabu(:,1)=(Randpos(1,1:m))'; 
    %%%%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游%%%%%%
    for j=2:n
        for i=1:m
            visited=Tabu(i,1:(j-1));  %已访问的城市
            J=zeros(1,(n-j+1));       %待访问的城市
            P=J;                      %待访问城市的选择概率分布
            Jc=1;
            for k=1:n
                if length(find(visited==k))==0
                    J(Jc)=k;
                    Jc=Jc+1;
                end
            end
            %%%%%%%%%%%%%%%%%%计算待选城市的概率分布%%%%%%%%%%%%%%%%
            for k=1:length(J)
                P(k)=(Tau(visited(end),J(k))^Alpha)...
                    *(Eta(visited(end),J(k))^Beta);
            end
            P=P/(sum(P));
            %%%%%%%%%%%%%%%%按概率原则选取下一个城市%%%%%%%%%%%%%%%%
            Pcum=cumsum(P);
            Select=find(Pcum>=rand);
            to_visit=J(Select(1));
            Tabu(i,j)=to_visit;
        end
    end
    if NC>=2
        Tabu(1,:)=R_best(NC-1,:);
    end
    %%%%%%%%%%%%%%%%%%%第四步：记录本次迭代最佳路线%%%%%%%%%%%%%%%%%%
    L=zeros(m,1);
    for i=1:m
        R=Tabu(i,:);
        for j=1:(n-1)
            L(i)=L(i)+D(R(j),R(j+1));
        end
        L(i)=L(i)+D(R(1),R(n));
    end
    L_best(NC)=min(L);
    pos=find(L==L_best(NC));
    R_best(NC,:)=Tabu(pos(1),:);
    %%%%%%%%%%%%%%%%%%%%%%%%%第五步：更新信息素%%%%%%%%%%%%%%%%%%%%%%
    Delta_Tau=zeros(n,n);
    for i=1:m
        for j=1:(n-1)
            Delta_Tau(Tabu(i,j),Tabu(i,j+1))=...
                Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
        end
        Delta_Tau(Tabu(i,n),Tabu(i,1))=...
            Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
    end
    Tau=(1-Rho).*Tau+Delta_Tau;
    %%%%%%%%%%%%%%%%%%%%%%%第六步：禁忌表清零%%%%%%%%%%%%%%%%%%%%%%
    Tabu=zeros(m,n);
    %%%%%%%%%%%%%%%%%%%%%%%%%历代最优路线%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:n-1
        plot([ C(R_best(NC,i),1), C(R_best(NC,i+1),1)],...
            [C(R_best(NC,i),2), C(R_best(NC,i+1),2)],'bo-');
        hold on;
    end
    plot([C(R_best(NC,n),1), C(R_best(NC,1),1)],...
        [C(R_best(NC,n),2), C(R_best(NC,1),2)],'ro-');  
    title(['优化最短距离:',num2str(L_best(NC))]);
    hold off;
    pause(0.005);
    NC=NC+1;    
end
%%%%%%%%%%%%%%%%%%%%%%%%%%第七步：输出结果%%%%%%%%%%%%%%%%%%%%%%%%%%
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:);            %最佳路线
Shortest_Length=L_best(Pos(1));             %最佳路线长度
figure(2),
plot(L_best)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

中 智能优化算法及其MATLAB实例（第二版）[包子阳，余继周][电子工业出版社][2018年01月][9787121330308]