我花了三个小时写了一道题的六千字题解....（POJ 2888 Magic Bracelet）

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

---

一道简单的题目

Problem 24.2.1 POJ 2888 Magic Bracelet / AcWing 3134. 魔法手链（（Burnside引理，矩阵快速幂优化DP，欧拉函数））

给定 $m$ 种不同颜色的魔法珠子，每种颜色的珠子的个数都足够多。

现在要从中挑选 $n$ 个珠子，串成一个环形魔法手链。

魔法珠子之间存在 $k$ 对排斥关系，互相排斥的两种颜色的珠子不能相邻，否则会发生爆炸。（同一种颜色的珠子之间也可能存在排斥）

请问一共可以制作出多少种不同的手链。

注意，如果两个手链经旋转后能够完全重合在一起，对应位置的珠子颜色完全相同，则视为同一种手链。

答案对 $9973$ 取模。
$1\le T\le 10$
$1\le n\le 10^9$
$\gcd (n,9973)=1$
$1\le m\le 10$
$0\le k\le \frac{m(m+1)}{2}$
$1\le a,b\le m$

Solution

这里因为多了很多互斥关系，也就是不同的循环之间有一定有了很多限制，所以不能使用 Polya 定理，只能使用 Burnside引理 。

本题比上一题简化了，只有循环这一种置换。我们可以发现 $n$ 很大，需要模 $9973$ ，并且保证 $\gcd (n,9973)=1$ 也就意味着我们最后除以 $n$ 的时候可以直接使用乘法逆元。

我们设旋转的距离为 $k=0,1,2,\cdots n-1$。

由于需要使用 Burnside引理，所以我们需要求一下不动点的数量。

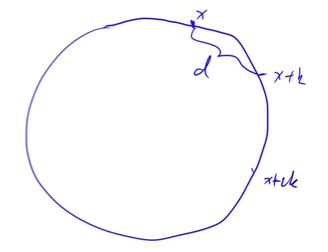
设一个点初始位置为 $x$ ，那么每转一次就会转到 $x+k$ 的位置

如图 24.2.1 所示

图 24.2.1

那么转多少会重复呢（回到起点，出现 循环）

回到起点不一定只赚一圈，可能需要转很多圈，由于点数是有限的，所以我们这样每次走 $k$ 步是一定会重复的。

这里很明显可以得到一个同余方程：

$x+kt\equiv x(\mathrm{m}\mathrm{o}\mathrm{d}n)$

$kt\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}n)$

即

$kt=nr+c$
$t=\frac{n}{d}$

其中 $d=\gcd (n,k)$

这也就意味着我们走 $\frac{n}{d}$ 步就会出现 循环

即：每一个循环一共有 $\frac{n}{d}$ 个点。

即：每个循环均使用了 $\frac{n}{d}$ 个点，而我们一共有 $n$ 个点，

所以一共会有 $\frac{n}{\frac{n}{d}}=d$ 个循环。

即我们仅有旋转这一种置换操作，会得到 $d=\gcd (n,k)$ 个循环。

我们发现 每个循环均有 $\frac{n}{d}$ 个点，我们可以先分析一个循环，其余的循环与该循环性质相同，分析一个循环即可得到所有的循环的答案。

我们发现了这一个循环的 $\frac{n}{d}$ 个点的一个性质：我们按照原本的点的编号的顺序看，任意两个相邻的点之间的距离均为 $d$ 。

---

证明： $d=\gcd (n,k)$

设 $k^{\prime }=\frac{k}{d}$，$n^{\prime }=\frac{n}{d}$。

由于我们每次走都是跳 $k$ 步，然后如果跳过了一圈长度为 $n$ 以后，就 $\%n$。因为 $k$ 和 $n$ 是 $d$ 的倍数，所以我们从起点 $x$ 出发，每次走到的点到起点的距离都必然是 $d$ 的倍数。然后因为我们一共走了 $\frac{n}{d}$ 步，而每一步又都是 $d$ 的倍数，也就是说我们每次走的就是距离可以写成表格，并且我们将 $0,d,2d\cdots$ 做一个映射:

距离   0  d  2d  3d  ...  (n / d - 1) * d = n - 1  
步数   0  1  2   3   ...           n / d           
映射   0  1  2   3   ...           n / d           

也就意味着我们每一步走的距离均为 $d$ 。

综上所诉，该性质得证 □

---

这个性质也就意味着对于每一个循环（我们当前分析的就是一个循环），我们只需要考虑 $d$ 的倍数的这 $\frac{n}{d}$ 个点即可。

所以我们仅考虑这些点的映射（$0,1,2,3,\cdots$），就会得到一个长度为 $n^{\prime }=\frac{n}{d}$ 的一个小环（共有 $n^{\prime }=\frac{n}{d}$ 个点），并且每次跳的距离是 $k^{\prime }$，其中 $k^{\prime }=\frac{k}{d}$，即 $k^{\prime }$ 与 $n$ 互质。也就可以证明这样跳，一定能遍历到这个小环的所有的点。

小环如图 24.2.2 所示

图 24.2.2

因为可以遍历这个小环的所有的点，可以得到：

$k^{\prime }\times 0,k^{\prime }\times 1,k^{\prime }\times 2,\cdots ,k^{\prime }\times (n-1)$ 构成了一个 $0$ ~ $n$ 的一个简化剩余系。（ 即该 $k^{\prime }$ 的序列在 $\mathrm{m}\mathrm{o}\mathrm{d}n$ 意义下还是 $0$ ~ $n-1$）

---

证明：

我们使用反证法。

假设$k^{\prime }\times 0,k^{\prime }\times 1,k^{\prime }\times 2,\cdots ,k^{\prime }\times (n-1)$ 不是$0$ ~ $n$ 简化剩余系，即序列中存在两个下标， $i\ne j$ 且 $k^{\prime }i=k^{\prime }j$

$k^{\prime }i=k^{\prime }j$

实际上就是：

$k^{\prime }(i-j)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}n)$

因为 $k^{\prime }$ 与 $n$ 互质，所以可以吧 $k^{\prime }$ 去掉

即：$i\equiv j(\mathrm{m}\mathrm{o}\mathrm{d}n)$

而 $0\le i,j<n$。

若 $i\equiv j(\mathrm{m}\mathrm{o}\mathrm{d}n)$，则定有 $i=j$，与前提不符，产生矛盾。

故对于所有的 $k^{\prime }i$，$k^{\prime }j$ ，$0\le i,j<n$，任意两个数均不相同，故在 $\%n$ 的意义下一定能遍历完 $0$ ~ $n-1$ 里的每一个数，故一定是 $0$ ~ $n-1$ 的一个简化剩余系。

综上所诉，该性质得证 □

---

由于我们刚刚得到的这一个循环的 $\frac{n}{d}$ 个点的一个性质：我们按照原本的点的编号的顺序看，任意两个相邻的点之间的距离均为 $d$ 。

以及另一个性质 $k^{\prime }\times 0,k^{\prime }\times 1,k^{\prime }\times 2,\cdots ,k^{\prime }\times (n-1)$ 构成了一个 $0$ ~ $n$ 的一个简化剩余系，也就意味着在 $\%n$ 的意义下一定能遍历完 $0$ ~ $n-1$ 里的每一个数

而我们仅考虑这些点的映射（$0,1,2,3,\cdots$），就会得到一个长度为 $n^{\prime }=\frac{n}{d}$ 的一个小环（共有 $n^{\prime }=\frac{n}{d}$ 个点），并且每次跳的距离是 $k^{\prime }$。我们再回代，即乘上一个 $d$ 以后，就意味着可以遍历所有与 $x$ 的距离为 $d$ 的倍数的点。

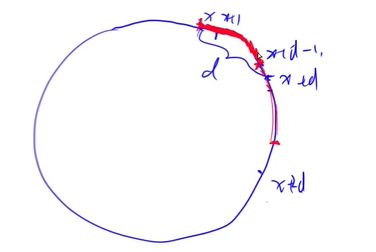
而最开始我们由得到了仅考虑旋转这一种置换，我们一共会有 $d$ 个循环，每次循环的步数（走的距离）均为 $d$ ，也就是每个循环的起点，为 $x,x+d,x+2d,\cdots$。

也就意味着第一个循环的区间为 $[x,x+d-1]$，第二个循环的区间为 $[x+d,x+2d-1]$，以此类推。我们之前说过，由于仅是旋转操作，得到的 $d$ 个循环的解法一摸一样，每一个循环的不动点的个数均相同，即为每一个循环内部的点的颜色按照顺序相同。

例如：第一个循环的颜色为 1 2 3 4 5 ，则第二个循环的颜色同样为 1 2 3 4 5 ，以此类推。

具体图形如图 24.2.3 所示：

图 24.2.3

因为每一个循环区间内部点的颜色都是相同的，也就意味着每个区间的最后一个点和下一个区间的第一个点相邻，而下一个区间的第一个点和这个区间的第一个点的颜色是相同的，所以我们就可以看作每个区间的最后一个点和该区间的第一个点是相邻的，也就意味着每个长度为 $d$ 的小区间又可以看作是一个循环，也就可以画成一个更小的圈。

也就意味着我们只需要讨论一下这个长度为 $d$ 的圈有多少个染色方案就行啦！

这个染色方案的数量就是这个置换的这个循环的不动点的数量。（因为这个圈固定以后，这一个段就固定了，那么这一小段的这个区间固定了以后，因为整个环分为 $d$ 段，也就是 $d$ 个循环，那么整个环也就固定了）

也就是说我们只需要求一下长度为 $d$ 的，满足要求的这个环的染色方案即可。

那么怎么求解这个方案数呢？我们仅需枚举一下这个环的起点

我们分情况讨论一下，我们枚举一下 $d$这个点是那种颜色，因为一共有 $m$ 种颜色，所以我们 $1$ ~ $m$ 枚举一遍。

我们求一下 $d$ 染乘 $1$ 的所有方案， $d$ 染 $2$ 的所有方案，$\cdots$ 到 $d$ 染 $m$ 的所有方案。

若 $d$ 染的颜色为 $i$ ，我们可以使用 DP 来求解这个答案。

$f[i][j]$ 表示的是染完了前 $i$ 个珠子的颜色，并且最后一个珠子的颜色为 $j$ 的所有方案的数量。

例如我们将 $d$ 染为 $i$，即 f[0][i] = 1，其余均为 $0$：f[0][1] = f[0][2] = ...f[0][m] = 0;。（$d$ 就是 $1$ 前面的这个珠子，编号为 $0$）

暴力转移即可：

f[i][j] += vis[k][j] ? f[i - 1][k] : 0;

其中 vis[k][j] 表示 $k$ 和 $j$ 是否互斥（由题目输入），如果不互斥的话说明 $k$ 和 $j$ 可以相邻。

最后的答案：分类讨论：

若 $d$ 染色为 $1$ ，答案为 f[d][1]。其余同理。

但是由于本题的 $n\le 10^9$ ，暴力转移无法通过，所以我们可以使用矩阵乘法来优化。

设 $F[i]=f[i][1...m]$

则 $F[i]=F[i-1]\ast M$

其中转移矩阵 M 就代表 若$k$ 和 $j$ 可以相邻，互不排斥，就为 $1$ ，否则就为 $0$ 。（该矩阵的转移方程实际上展开以后就是上面的DP转移方程）

则答案 $F[d]=F[0]\ast M^d$，我们可以来使用快速幂优化。

总时间复杂度为 $O(M^{3}logn)$

最后一个问题，因为 $n$ 很大，所以我们枚举 $k$ 的时候不可能直接枚举。

我们发现 $k$ 的唯一作用就是得到 $d=\gcd (n,k)$，而我们非常容易就可以发现很多 $gcd(n,k)$ 是相同的，因此我们就可以将 $k$ 按照所有的最大公约数分类，也就是直接枚举$\gcd (n,k)$ 即可，也即是说我们只需要枚举 $n$ 的约数即可，那么就意味着最多只会有 $\phi (n\le 10^9)\le 1600$ 种。

则对于所有的 $d=\gcd (n,k)$ 都可以直接使用快速幂来求解。分类之后我们肯定要算一下每一个 $d$ 都包含了多少个 $k$，换句话说就是一共有多少个 $k$ 满足 $\gcd (n,k)=d$ 呢？

我们发现这就是一个 非常经典的欧拉函数问题。

$\gcd (n,k)=d$

即：$\gcd (\frac{n}{d},\frac{k}{d})=1$ 的个数，也就是在$0$ ~ $\frac{n}{d}$ 种互质的个数，也就是 $\phi (\frac{n}{d})$。直接暴力求，复杂度 $O(\sqrt{\phi (\frac{n}{d}})$。

这里的答案（所有不动点的和）就是 $$ans=\sum _{d=0}^{n}F[0]\ast M^d\ast \phi (\frac{n}{d})$$

最后的答案就是所有不动点的平均值即不动点个数和除以所有置换的个数。

因为我们这里的置换是旋转，一共有 $n$ 个点，所以一共有 $n$ 种置换

即最后的答案为：$\frac{ans}{n}$，也就是乘上 $n$ 模 $9973$ 的逆元 $ans\times inv(n)$

Code

#include 
#include 
#include 

using namespace std;

const int N = 11, P = 9973;

int m;
struct Matrix
{
     
    int a[N][N];
    Matrix()
    {
     
        memset(a, 0, sizeof a);
    }
};

Matrix operator* (Matrix a, Matrix b)
{
     
    Matrix c;
    for (int i = 1; i <= m; i ++ )
        for (int j = 1; j <= m; j ++ )
            for (int k = 1; k <= m; k ++ )
                c.a[i][j] = (c.a[i][j] + a.a[i][k] * b.a[k][j]) % P;
    return c;
}

int qmi(Matrix a, int b)
{
     
    Matrix res;
    for (int i = 1; i <= m; i ++ ) res.a[i][i] = 1;
    while (b)
    {
     
        if (b & 1) res = res * a;
        a = a * a;
        b >>= 1;
    }

    int sum = 0;
    for (int i = 1; i <= m; i ++ ) sum += res.a[i][i];
    return sum % P;
}

int phi(int n)
{
     
    int res = n;
    for (int i = 2; i * i <= n; i ++ )
        if (n % i == 0)
        {
     
            res = res / i * (i - 1);
            while (n % i == 0) n /= i;
        }
    if (n > 1) res = res / n * (n - 1);
    return res % P;
}

int inv(int n)
{
     
    n %= P;
    for (int i = 1; i < P; i ++ )
        if (i * n % P == 1)
            return i;
    return -1;
}

int main()
{
     
    int T;
    cin >> T;
    while (T -- )
    {
     
        int n, k;
        cin >> n >> m >> k;
        Matrix tr;
        for (int i = 1; i <= m; i ++ )
            for (int j = 1; j <= m; j ++ )
                tr.a[i][j] = 1;
        while (k -- )
        {
     
            int x, y;
            cin >> x >> y;
            tr.a[x][y] = tr.a[y][x] = 0;
        }
        int res = 0;
        for (int i = 1; i * i <= n; i ++ )
            if (n % i == 0)
            {
     
                res = (res + qmi(tr, i) * phi(n / i)) % P;
                if (i != n / i)
                    res = (res + qmi(tr, n / i) * phi(i)) % P;
            }
        cout << res * inv(n) % P << endl;
    }
    return 0;
}

讲完啦！六千字的题解，快写死我了，你看懂了嘛？(●ˇ∀ˇ●)

看不懂没关系，点个赞就懂了 =￣ω￣=