『最短路径』单源无负权值最短路径算法——Dijkstra算法（优先队列优化 + C++实现 + 例题）

『算法原理』

---

最短路径（Shortest Path）：一个结点到另一个结点的最小权值和。

Dijkstra算法同时也叫单源最短路算法，其思想是——按路径长度递增的次序产生最短路的算法。

通俗来讲就是，找出从源点开始通过1条边可以到达的点的最小路径，2条边可以到达的点的最小路径，....，n-1条边可以到达的点的最小路径，将权值最小的点加入到集合S中，一直更新到终点位置，找到源点和终点的最小路径，将所有结点都加入到S中，结束算法。和Prim算法十分类似。

算法步骤如下：

a.找到一个源点s，更新源点和其他结点的距离（权值），如果不能直接到达就先赋值为无穷大，将源点加入到集合S。

b.更新从源点出发最多经过1条边就可以到达的点的最小权值，将权值最小的点加入到集合S，最多2条边就可以的点的最小权值，...，最多n-1条边就可以的点的最小权值，将权值最小的点加入到集合S。

c.把所有的结点都加入到集合S中，找到源点和终点的最短路径，结束算法。

【算法图示】

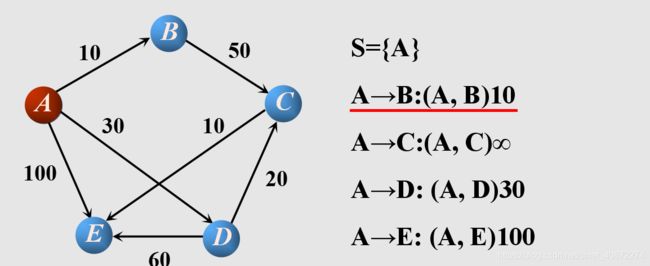
  对于图G：

 a.选择一个源点A，更新A到B，C，D，E的距离，将A加入到集合S中

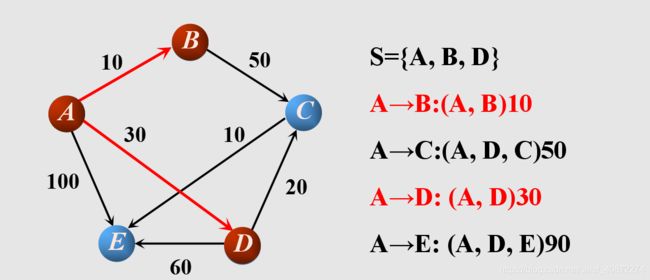
b(1).更新从源点开始通过1条边就可以到达的点，找到其中的权值最小的点B，更新到各结点的权值，将B加入到集合S中

 b(2).更新从源点开始最多通过2条边就可以到达的点，找到未加入到集合S的结点中的权值最小的点D，更新到各结点的权值，将D加入到集合S中

找到未加入到集合S的结点中的权值最小的点C，更新到各结点的权值，将C加入到集合S中

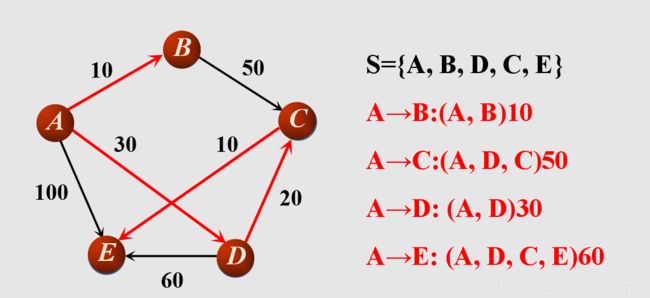
 b(3).更新从源点开始最多通过3条边就可以到达的点， 找到未加入到集合S的结点中的权值最小的点E，更新到各结点的权值，将E加入到集合S中

算法结束。

『算法模板』

 

【朴素模板】

#include 
#include 
using namespace std;
const int N = 107,INF= 0x3f3f3f3f;
int map[N][N],n,m;

void dijstra(){
	int i,j,min,u;
	int d[N],vis[N];
	//d数组表示从原点到i点的最短距离
	//vis用于表达这个点是否已经被选中
	for(i=1;i<=n;i++){
		d[i]=map[1][i];
		vis[i]=0;
	}
	vis[1] = 1;
	for(i=1;i<=n-1;i++){
		min=INF;
		for(j=1;j<=n;j++)		//每次找点的过程，首先这个点没有被发现，然后找一个最小点
			if(vis[j]==0 && d[j] d[u]+map[u][v]) //对每个点依次进行松弛操作 
					d[v] = d[u]+map[u][v];
	}
	printf("ans = "); 
	for(i=1;i<=n;i++)
		printf("%d ",d[i]);
}
int main(){	
	scanf("%d %d",&n,&m);
	for(int i = 1; i <= n; i++)
		for(int j =1; j<=n; j++)
			if(i == j) map[i][j] = 0;
			else map[i][j] = INF;
	for(int i = 1,u,v,w; i <= m; i++){
		scanf("%d %d %d",&u,&v,&w);
		//printf("%d %d %d\n",u,v,w);
		map[u][v] = w;
	}
	dijstra();
	return 0;
 
}
/*
5 9 1
1 2 10
1 3 3
2 3 1
2 4 2
3 2 4
3 4 8 
3 5 2
4 5 7
5 4 9 
ans:0 7 3 9 5 
*/

【使用堆(priority_queue)优化+vector存图】

/*****************************
*author:ccf
*source:
*topic:shortest_path_dijkstra_que
*tip:邻接表使用vector
*******************************/
#include 
#include 
#include 
#include 
#include 
#include 
#include  
#define ll long long
using namespace std;

const int N = 5e5+7;
const int INF = 2147483647;
int n,m,s;
int dis[N]; //dis[i] 为源点到i点的最短路径 
bool vis[N] = {0};//vis[i] = 1,证明 i 已经确定了最短路 
struct Node{
	int v;//端点的编号 
	int w;//权值 
	bool operator < (const Node& b) const{
		return w > b.w;   //priority_queue总是将最大的元素出列
	}
}node;
vector > G; 

void dijkstra(int s){
	priority_queue pq;
	node.v = s;//放入起点 
	node.w = 0;
	pq.push(node);
	dis[s] = 0;
	while(pq.size()){
		Node tp = pq.top();pq.pop();//获取堆顶
		int u = tp.v,vv; //u是已经确认最短路径的点编号，vv是没有确认的点的编号 
		if(vis[u]) continue;
		vis[u] = true;
		int len = G[u].size();
		for(int i = 0; i < len; ++i){
			vv = G[tp.v][i].v;
			if(vis[vv]) continue;
			if(dis[vv] > dis[u] + G[u][i].w){//松弛操作 
				dis[vv] = dis[u] + G[u][i].w;
				node.v = G[u][i].v,node.w = dis[vv];
				pq.push(node);
			}
		}
	}
}

int main(){
	freopen("data.in","r",stdin);
	scanf("%d %d %d",&n,&m,&s);
	G.resize(n+7);
	G.clear();
	for(int i = 1; i <= n; i++) dis[i] = INF;
	for(int i = 1,u,v,w; i <= m; ++i){
		scanf("%d %d %d",&u,&v,&w);
		node.v = v;
		node.w = w;
		G[u].push_back(node);
	}
	dijkstra(s);
	for(int i = 1; i <= n; ++i)
		printf("%d ",dis[i]);
	return 0;
}

【使用堆(priority_queue)优化+链式前向星存图】

/*****************************
*author:ccf
*source:POJ-
*topic:
*******************************/
#include 
#include 
#include 
#include 
#include 
#include  
#define ll long long
using namespace std;

const int N = 1e4+7,M = 5e5+7;
const int INF = 2147483647;
int n,m,s;
int dis[N]; //dis[i] 为源点到i点的最短路径 
bool vis[N] = {0};//vis[i] = 1,证明 i 已经确定了最短路 
int head[N],nex[M],to[M],eg[M],cnt_e = 0;
struct Node{
	int v;//端点的编号 
	int w;//权值 
	bool operator < (const Node& b) const{
		return w > b.w;   //priority_queue总是将最大的元素出列
	}
}node;
void addedge(int u,int v,int w){
	nex[++cnt_e] = head[u];
	head[u] = cnt_e;
	to[cnt_e] = v;
	eg[cnt_e] = w;
}
void dijkstra(){
	for(int i = 1; i <= n; i++) dis[i] = INF;
	priority_queue pq;
	node.v = s;
	node.w = 0;
	pq.push(node);
	dis[s] = 0;
	while(pq.size()){
		int u = pq.top().v;
		pq.pop();
		if(vis[u]) continue;
		vis[u] = true;
		for(int i = head[u],vv; i; i = nex[i]){
			vv = to[i];
			if(dis[vv] > dis[u] + eg[i]){
				dis[vv] = dis[u] + eg[i];
				//node.w = dis[vv];node.v = vv;
				pq.push((Node){vv,dis[vv]});
			}
		}
	}
}

int main(){
	//freopen("data.in","r",stdin);
	scanf("%d %d %d",&n,&m,&s);
	for(int i = 1,u,v,w; i <= m; ++i){
		scanf("%d %d %d",&u,&v,&w);
		addedge(u,v,w);
	}
	dijkstra();
	for(int i = 1; i <= n; ++i)
		printf("%d ",dis[i]);
	return 0;
}

例题：洛谷 P3371 【模板】单源最短路径（弱化版）https://www.luogu.com.cn/problem/P3371