c++ 遍历所有点且距离最短_最短路径问题Dijkstra算法详解
1、Dijkstra算法介绍
·
算法起源:
·
Djkstra 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-Source Shortest Path)的算法,由计算机科学家Edsger Djkstra于1956年构思并于1959年发表。其解决的问题是:给定图和源顶点v,找到从v至图中所有顶点的最短路径。
·
算法特点:
·
Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
·
基本思想
·
1.通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
2.此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
3.初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是”起点s到该顶点的路径”。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。… 重复该操作,直到遍历完所有顶点。
·
操作步骤
·
1.初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
2.从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
3.更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
4.重复步骤(2)和(3),直到遍历完所有顶点。
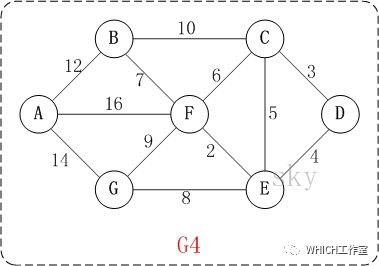
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
图解2.
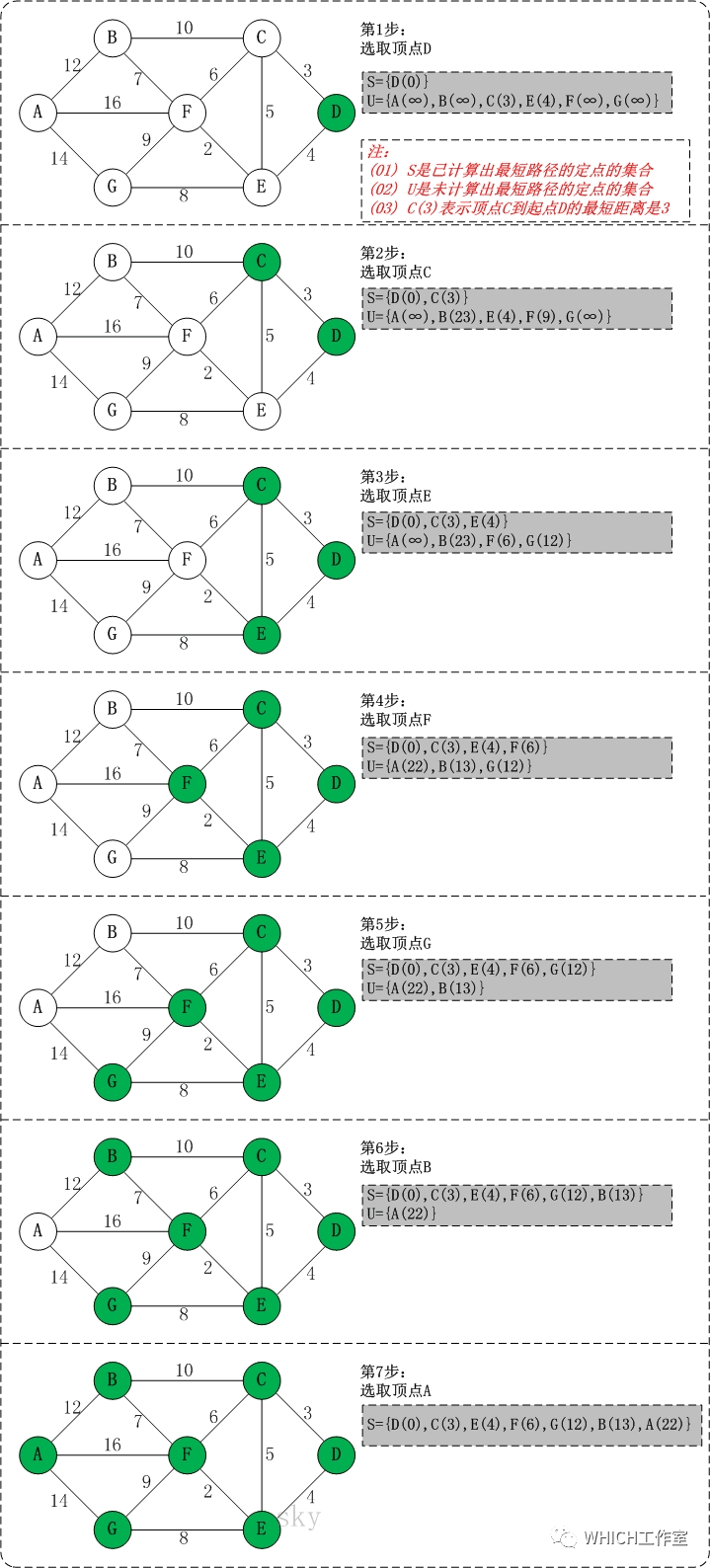
以下B节点中23应为13。
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
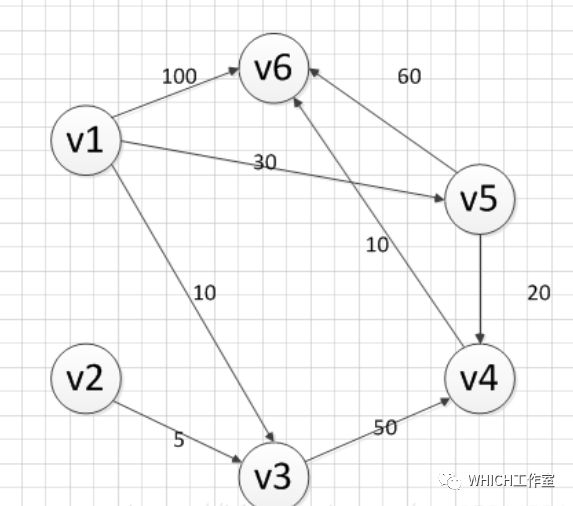
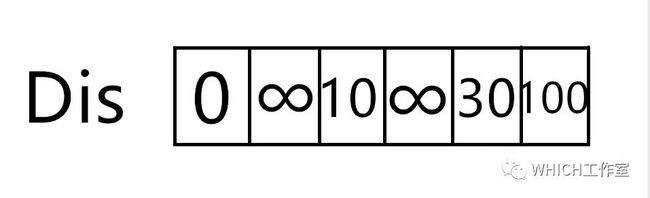
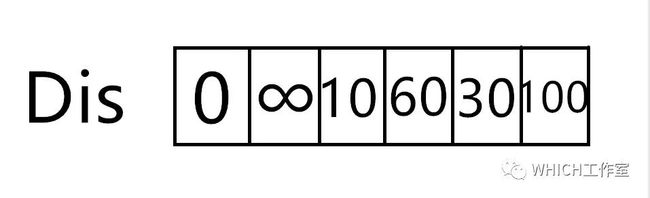
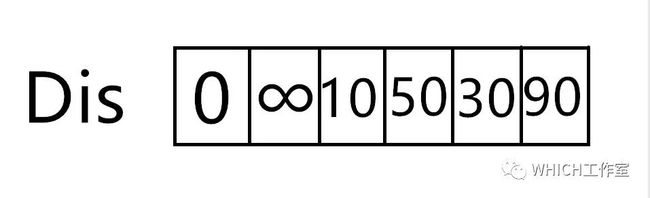
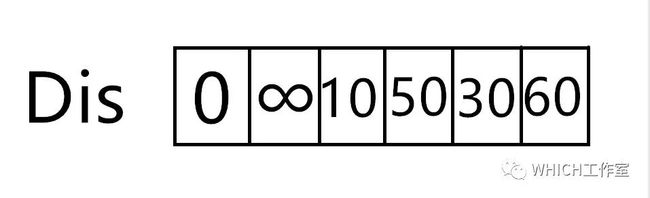
图解2.
求从顶点v1到其他各个顶点的最短路径
这个图解相对简单,易于理解
我们最后得到的结果为:
起点 终点 最短路径 长度v1 v2 无 ∞ v3 {v1,v3} 10 v4 {v1,v5,v4} 50 v5 {v1,v5} 30 v6 {v1,v5,v4,v6} 60附加一道例题供大家练习:
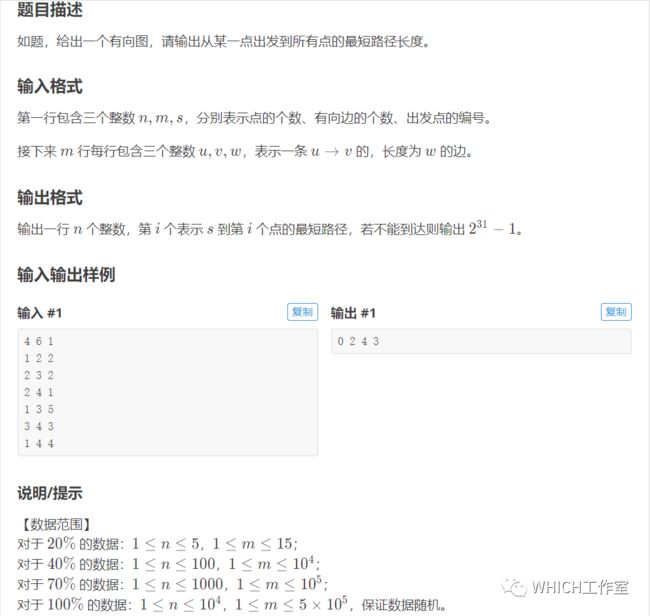
洛谷 P3371 【模板】单源最短路径
参考代码如下:
#includeusing namespace std;#define maxn 10005#define maxm 500005#define INF 1234567890inline int read(){
int x=0,k=1; char c=getchar(); while(c'9'){if(c=='-')k=-1;c=getchar();} while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar(); return x*k;}struct Edge{
int u,v,w,next;}e[maxm];int head[maxn],cnt,n,m,s,vis[maxn],dis[maxn];struct node{
int w,now; inline bool operator //重载运算符把最小的元素放在堆顶(大根堆) {
return w>x.w;//这里注意符号要为'>' }};priority_queueq;//优先队列,其实这里一般使用一个pair,但为了方便理解所以用的结构体inline void add(int u,int v,int w){
e[++cnt].u=u; //这句话对于此题不需要,但在缩点之类的问题还是有用的 e[cnt].v=v; e[cnt].w=w; e[cnt].next=head[u]; //存储该点的下一条边 head[u]=cnt; //更新目前该点的最后一条边(就是这一条边)}//链式前向星加边void dijkstra(){
for(int i=1;i<=n;i++) {
dis[i]=INF; } dis[s]=0; //赋初值 q.push((node){0,s}); while(!q.empty()) //堆为空即为所有点都更新 {
node x=q.top(); q.pop(); int u=x.now; //记录堆顶(堆内最小的边)并将其弹出 if(vis[u]) continue; //没有遍历过才需要遍历 vis[u]=1; for(int i=head[u];i;i=e[i].next) //搜索堆顶所有连边 {
int v=e[i].v; if(dis[v]>dis[u]+e[i].w) {
dis[v]=dis[u]+e[i].w; //松弛操作 q.push((node){dis[v],v}); //把新遍历到的点加入堆中 } } }}int main(){
n=read(),m=read(),s=read(); for(int i=1,x,y,z;i<=m;i++) {
x=read(),y=read(),z=read(); add(x,y,z); } dijkstra(); for(int i=1;i<=n;i++) {
printf("%d ",dis[i]); } return 0;}文中很多干货,写这篇文章目的就是希望这篇文章可以帮到有需要的人。希望喜欢的同学可以多多转发到朋友圈、点击文章右下角“在看”,这就是对我们最大的鼓励啦,谢谢支持。