对抗攻击经典论文剖析(下)【DeepFool、One pixel attack、Universal adversarial perturbations、ATN】
引言
上一篇讲的几篇经典对抗攻击论文主要讲的是如何在梯度上扰动或者优化,即尽可能保证下的扰动,不被人类发现,却大大降低了模型的性能。这一篇我们将会有一些更有意思的对抗攻击样本生成,包括像素级别的扰动以及样本生成(DeepFool、One pixel attack、Universal adversarial perturbations、ATN)。
DeepFool: a simple and accurate method to fool deep neural networks
动机
文章作者思考究竟对原始图像做了多大修改就可以欺骗AI模型呢?换个说法就是,如何尽量少的修改原始图像就可以达到欺骗AI模型的目的呢,换言之就是扰动大小多少合适,取值大小这会对算法效果产生很大影响,那么今天的这个算法可以避免这个问题。
算法
文章首次提出了一个分类器鲁棒性的评估指标,对于图像样本 x x x,分类器$ k ^ ( ⋅ ) \hat k\left( \cdot \right) k^(⋅),对抗扰动 r r r,那么该分类器在 x x x鲁棒性评价指标为:
![]()
对于二分类问题:
设分类边界为: ℓ = { x : f ( x ) = 0 } \ell = \left\{ {x:f\left( x \right) = 0} \right\} ℓ={ x:f(x)=0},扰动向量为 r ( x 0 ) = arg min ∥ r ∥ 2 r\left( { {x_0}} \right) = \arg \min {\left\| r \right\|_2} r(x0)=argmin∥r∥2,其中 s i g n ( f ( x 0 + r ) ) ≠ s i g n ( f ( x 0 ) ) = − f ( x 0 ) ∥ w ∥ 2 w sign\left( {f\left( { {x_0} + r} \right)} \right) \ne sign\left( {f\left( { {x_0}} \right)} \right) = - { {f\left( { {x_0}} \right)} \over { { {\left\| w \right\|}_2}}}w sign(f(x0+r))=sign(f(x0))=−∥w∥2f(x0)w。
我们借助原图的示例来理解公式
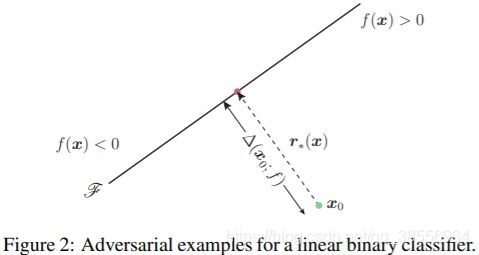
所以上面的公式就可以理解为样本到分类边界的最短距离。
对于多分类问题:
多分类问题可以看作由许多二分类问题的共同作用。如同二分类一样,我们需要得到一个点和某分类函数边界的最小距离。
l ^ ( x 0 ) = arg min k ≠ k ^ ( x 0 ) ∣ f k ( x 0 ) − f k ^ ( x 0 ) ∣ ∥ w k − w k ^ ∥ 2 \hat l\left( { {x_0}} \right) = \arg \mathop {\min }\limits_{k \ne \hat k\left( { {x_0}} \right)} { {\left| { {f_k}\left( { {x_0}} \right) - {f_{\hat k}}\left( { {x_0}} \right)} \right|} \over { { {\left\| { {w_k} - {w_{\hat k}}} \right\|}_2}}} l^(x0)=argk=k^(x0)min∥∥wk−wk^∥∥2∣∣fk(x0)−fk^(x0)∣∣
用论文中的图示理解如下:

实验
从上面的实验结果来看,deepfool明显优于FGSM,无论是攻击真确率还是在降低扰动方面。
One pixel attack for fooling deep neural networks
动机
作者首先思考一下像素级别攻击可行的原因。
- 自然图像邻域的分析,以前通过限制固定干扰向量长度分析自然图片的邻域。比如,通用扰动在每个像素上添加一些小的变化,在图像的周围获得球形范围内的对抗样本。同时,少量像素扰动可以看做是对输入空间以较低维度进行切分,与DNN网络中高维度提取输入特征不同。
- 实际过程中,攻击可以对隐藏的对抗信息有效果。前人的工作没有可以保证做的改变不被人观察到。一种直接方式是尽可能少的修改扰动量。本文提出了简单的限制扰动像素的个数,而不是增加额外的限制条件与设计复杂的损失函数构建扰动,换言之,本文通过控制扰动像素的个数而不是扰动向量来评估扰动的强度。考虑了最差情形,单个像素的条件。
贡献
本文提出了一个黑盒DNN攻击,仅扰动一个差分进化的单个像素,而其中唯一可用的信息是概率标签。贡献如下:
(1)有效性,在CIFAR-10数据集上,在三个常见的网络结构框架上进行无目标攻击,有效率为68.71%,72.85%,63.53%。平均每个图片可以被扰动为1.9,2.3和1.7个其他的类别。在ImageNet上BVLC和AlexNet模型攻击的有效率为41.22%。
(2)半黑盒攻击:只需要返回概率标签,而不需要返回想梯度和网络结构等内部信息等。本文只考虑了概率标签,而不是所有明确目标的抽象化。
(3) 灵活性:可以对梯度难以计算和不可微的网络进行攻击。
算法定式
对抗图片的生成可以看作是一个带条件的优化问题,假定每个图片可以由向量表示,每个向量中的元素代表图像的一个像素值。 f f f作为目标图像分类器,接受一个 n n n维的输入,则 x = ( x 1 , x 2 , ⋯ , x n ) x = \left( { {x_1},{x_2}, \cdots ,{x_n}} \right) x=(x1,x2,⋯,xn)代表原始正确分类为 t t t的图片,我们根据原始样本人为设计的干扰样本为 e ( x ) = ( e 1 , e 2 , ⋯ , e n ) e\left( x \right) = \left( { {e_1},{e_2}, \cdots ,{e_n}} \right) e(x)=(e1,e2,⋯,en),那么对于攻击性问题,主要是优化以下的方程:
m a x i m i z e f a d v ( x + e ( x ) ) { {\mathop{\rm maximize}\nolimits} {f_{adv}}\left( {x + e\left( x \right)} \right)} maximizefadv(x+e(x))
s u b j u e c t − t o ∥ e ( x ) ∥ ≤ L {subjuect - to\left\| {e\left( x \right)} \right\| \le L} subjuect−to∥e(x)∥≤L
问题主要分为两个部分(1)需要干扰的维度(2)每个维度需要干扰多大的量,本文有点不同,对于单像素,d为1,先前的工作需要修改部分像素。 对于单像素的修改可以看作是沿着n维向量中的一个平行的方向对数据点进行扰动。一般来说少量的像素攻击,在输入切片低维上造成扰动。实际上,并不关心扰动的强度,单个像素可以对图片中的n个方向进行多个维度任意强度的攻击,如下图所示:

差分进化(DE) 差分进化算法是解决复杂多模型优化问题的优化算法。DE属于一般的进化算法,在population select阶段可以保持多样性,实际中相比梯度和其他进化算法,更加高效的寻找可行解,在每次迭代过程中,根据当前的population(father)生成候选解集合(child)。每个子类与其对应的父类进行比较,如果比父类更适合,则可以留存下来。这样,只与父类和子类进行比较,在保持多样性同时可以获得较高的稳定值。由于,DE不需要梯度的信息进行优化,因此,不要求目标函数是已知的或者是可微分的。比梯度下降方法可应用的问题更广(像不可分,动态噪音等)。基于DE算法进行对抗图像的生成有以下几个优点:
I.可以以更大的概率找到全局最优解
II.需要得信息更少。
III简易性。
实验
首先说一下评价指标。
Success Rate: 在非目标攻击的情况下,被定义为对抗图像被成功分为任意其他类别的比例。 在目标攻击的情况下,它被定义为将图像扰动为一个特定目标类的概率。
Adversarial Probability Labels(confidences):累加每次成功扰动为目标类别概率值,然后除以成功扰动的总数。表示模型对对抗图像产生“误分类”的confidence。
Number of target classes 计算成功扰动到一定数量类别的图片的数量。尤其,计算无法被其他类别扰动的图片数量,可以评估非目标攻击的有效性。

当然攻击的像素数目越多越好!
Adversarial Transformation Networks: Learning to Generate Adversarial Examples
动机
在现有的许多方法中,利用梯度信息进行攻击的方法占绝大多数,本文另辟蹊径,提出了另一种方法:训练一个深度网络,将原图作为输入,输出为对抗样本。
算法

f ( x ) f\left( x \right) f(x)是训练好用于分类的网络,也就是我们攻击的目标。
g f , θ ( X ) {g_{f,\theta }}\left( X \right) gf,θ(X)是我们要训练的生成网络,输入为原始样本,输出为对抗样本。
L x {L_x} Lx是一种损失函数,在文中是 L 2 {L_2} L2 Loss。
本文中提到的两种生成方法。

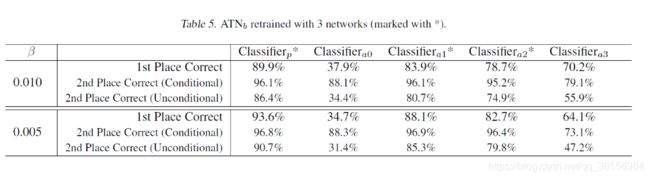
实验
作者考虑在攻击时,同时选择多个Model进行攻击,训练方式与之前大致相同,只是在此时需要同时对多个Model分别进行计算,再最小化。以发现,攻击训练时包括的模型时,其攻击成功概率大大提升,且还增加了对其他未包括的模型的攻击泛化能力。因此,如果在训练时加入大量的模型进行攻击,其产生的对抗样本的迁移能力是有很大的概率得到提升的。
Universal adversarial perturbations
动机
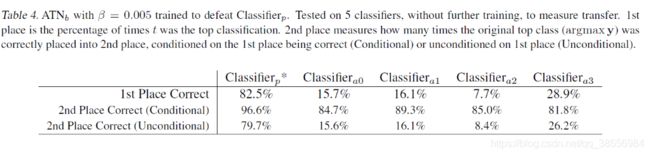
对于任意给定的高效DNN分类器,作者都能为输入图片施加一个扰动,使得分类器以较大概率分类错误,从而实现对于dCNN的攻击。这个“扰动”有两个特点:1.universal,即扰动与输入图片无关,仅与模型本身相关。2.very small,具有小的范数,从而不改变图片本身的结构。另外,作者提出了一个算法,使得对于不同的模型VGG、GoogLeNet、ResNet等都很容易计算出各自对应的扰动。
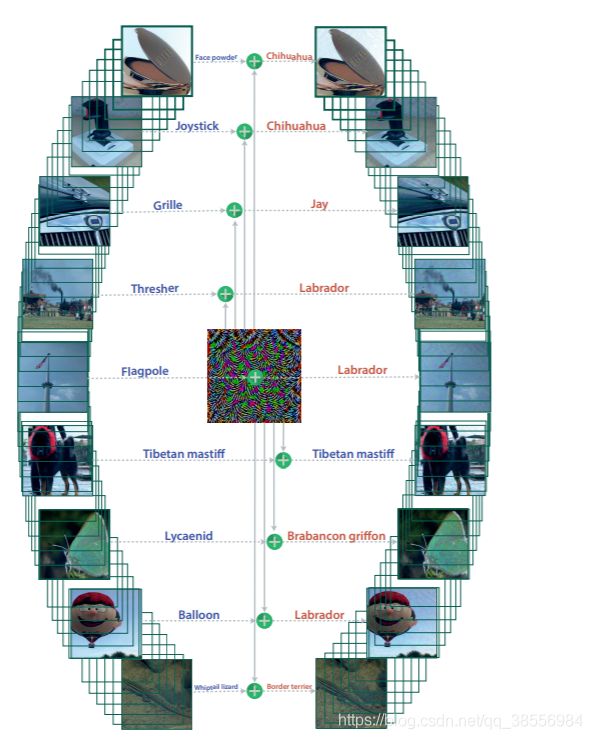
文章工作
本文的工作包括:
- 说明了通用扰动确实存在
- 提出了扰动生成算法
- 展示了扰动优异的泛化性能(通过较小的样本图片集合就能生成扰动)
- 展示扰动不仅对于输入图片是universal,对于网络架构同样是universal
- 分析了universal perturbations可用于攻击DNN的一些数学解释
算法
设采样的图片集合为 X = { x 1 , x 2 , ⋯ , x m } X = \left\{ { {x_1},{x_2}, \cdots ,{x_m}} \right\} X={ x1,x2,⋯,xm}, K ^ \hat K K^是分类器函数,我们
令扰动向量为 v v v,则要满足以下约束:
∥ v ∥ p ≤ ε {\left\| v \right\|_p} \le \varepsilon ∥v∥p≤ε
P x ∼ μ ( k ^ ( x + v ) ≠ k ^ ( x ) ) ≥ 1 − δ { {\rm P}_{x \sim \mu }}\left( {\hat k\left( {x + v} \right) \ne \hat k\left( x \right)} \right) \ge 1 - \delta Px∼μ(k^(x+v)=k^(x))≥1−δ
其中 ε \varepsilon ε为控制扰动的范数, δ \delta δ为欺骗率。
扰动算法的生成是基于初始为0的扰动迭代生成最佳的扰动的:

整个算法流程图如下: