精度验证的样本_基于IRVM的锂电池荷电状态评估方法与仿真验证
电动汽车动力电池在使用过程中表现出高度的非线性,其动力电池的荷电状态(State of Charge,SOC)SOC受多因素影响,无法通过传感器直接测量,而是必须通过测量电池电压、工作电流、电池内阻和温度等其他物理量并采用一定的数学模型和算法估计得到[1]。
近年来,支持向量机方法(Support Vector Machine,SVM)已广泛应用于锂离子电池SOC预测领域[2],但SVM算法稀疏性性有限,且只能进行单点预测,缺乏不确定性表达和管理能力。基于SVM 算法并结合概率学习的稀疏贝叶斯理论和最大似然法提出的相关向量机[3](Relevance Vector Machine,RVM)算法,其稀疏性较高,可以提供概率性预测结果,实现区间预测,具有自动参数设置和任意使用核函数等优点。RVM算法进行数据回归分析时,可以通过参数调整来对过拟合和欠拟合过程进行灵活控制。
RVM是一种适合锂离子电池预测的机器学习方法,文献[4]利用电池放电电压的样本熵作为输入数据并采用RVM算法直接实现了锂离子电池RUL 预测,较SVM获得了更高的预测精度;文献[5]选择测量电压、测量电流和表面温度作为输入数据,输入数据经过滤波归一化等预处理,直接用RVM算法对SOC进行预测,较SVM获得了更高的预测精度。
但由于RVM过于稀疏及采集的数据存在动态波动特性,导致直接采用RVM进行锂离子电池SOC预测,预测结果的稳定性差。本文首先分析了RVM算法预测精度的影响因素,并结合增量学习算法构建了一种改进的增量相关向量机算法(Incremental improved RVM,IRVM),改善了RVM算法多步预测能力差的问题,并将其应用于锂离子电池SOC评估预测领域。为了验证研究方法的适用性和有效性,研究采用欧洲的NEDC和日本的1015两典型工况数据为参照,对比分析了IRVM算法和完全重新训练的相关向量机(Retraining RVM,RRVM)算法的预测效果和性能,结果表明提出的改进的IRVM针对锂离子电池SOC预测具有较好预测效果,为该方法在锂离子电池SOC预测领域提供思路和借鉴。
1 相关向量机方法基本原理
对于给定的训练样本输入集X={x1,x2,…,xN}和对应的样本输出集T={t1,t2,…,tN},N为训练样本数,RVM的回归模型可定义为:

其中,Lb和Ub分别为预测值的下限和上限;zα/2为正态分布的双侧α分位点。
2 锂离子电池IRVM荷电状态分析
增量学习算法随在线样本的到来动态更新预测模型,具有较高的预测精度。SYED N A等提出的增量SVM算法[7],节省了大量的时空消耗,但由于在重新训练的过程中丢失了过多的支持向量,该算法的精度较差。
相比于SVM算法,RVM算法的相关向量十分稀疏,且具有概率式输出的特点,因此采用增量学习算法对RVM算法的输出影响不大[8]。图1所示为IRVM算法流程示意图,其中,TS为训练样本集;NS为预测样本集,NS=[NX,NY];RS为相关向量集,RS=[RX,RY];Error为预测的最大绝对误差,ynew为预测值。

针对锂离子电池SOC的IRVM预测评估,可以概括为以下主要步骤:
(1)初始化数据集和RVM参数;
(2)RVM训练,获得训练值yxun、相关向量集RS;
(3)判断训练值yxun是否达到精度要求,若未达到,调整核参数,重新训练;否则,获得RVM的模型,并输入新增样本NX进行预测,输出预测值ynew;
(4)判断预测值ynew是否达到精度要求,未达到,则构造新的训练集TS=RS∪NS,重新训练RVM,更新RVM模型;否则保持RVM模型不变,继续预测,直到所有数据预测完成。
3 IRVM荷电状态评估验证与结果讨论
3.1 核参数BW和训练样本数对预测效果的影响
为了验证所建立的IRVM算法的预测效果,研究数据集来源于ADVISOR软件平台,选用gm_ev1_in车型、ESS_L17_temp型号的锂离子电池(25 ℃条件下,7.035 Ah)、rint电池模型,其他参数均为默认设置,获取NEDC工况和1015工况的电压、电流、温度和SOC数据。
验证分析选用NEDC工况的数据,共1 826组,输入数据为锂离子电池的电压、电流和温度,输出数据为SOC。RVM的核函数选择常用的高斯核函数,噪声方差σ2=var(y)*0.1,分别规定训练样本为200、400和600,预测步长为200、400和600,核参数BW过小预测精度较低,因此设置BW从10开始,增长率为1,最大值为40。预测精度的评价选用平均绝对误差AME,如式(5)所示,其中,Y为SOC的真实值,Y′为SOC的预测值,n为预测步长。
分别用以上三个训练样本依次进行实验,分析核参数BW和训练样本数对预测效果的影响,仿真结果如图2所示。

图2为不同训练样本数预测结果对比图,其中横坐标为核参数,纵坐标为预测的平均绝对误差,三幅图的预测步长分别为200、400和600。
由图2可知:
(1)核参数的大小影响RVM的预测精度,核参数过小,其预测误差过大,三幅图中核参数BW在35~40时的预测效果优于20之前,在20~35之间时预测效果最好,且当BW=35时,三种训练样本的预测误差同时达到低峰,此时的预测精度受训练样本数和预测样本数的影响较小,可以改善由训练样本数不足和预测步长过长对预测结果影响,是预测模型中核参数的最优值。
(2)不同训练样本数N对预测结果影响较大,三幅图均表明,当N为400时,预测效果最好。图2(a)中,预测步长为200,其预测精度受训练样本数的影响,N越小,预测精度越低;图2(b)中,预测步长为400,此时N为200和600时的预测精度相差较小,N=600时的预测精度较好;图2(c)中,预测步长为600,此时N=600时的预测精度低于N=200时。由此可见,训练样本数过大或过小均影响预测精度,N=400时的预测精度最好。
(3)不同的预测步长对预测结果影响较大,预测步长越大,预测精度越低,故RVM算法的多步预测能力差。
综上所述,核参数BW、训练样本数和预测步长均影响RVM算法的预测效果,合理设置这三个参数可以改善算法的预测精度,减少IRVM算法重新训练的次数,提高算法的计算效率。
3.2 IRVM算法的适应性和有效性验证
为了进一步验证本文所提出方法的适用性和有效性,和RRVM算法进行对比,采用NEDC和1015两个工况数据进行仿真分析以对其进行验证。核函数选择常用的高斯核函数,核参数BW为40,噪声方差σ2=var(y)·0.1,误差限Error=0.04,根据3.1小节的分析,训练样本数选择400左右,预测步长为50。
对SOC的预测精度进行评价,评价的标准采用最大绝对误差maxe和均方根误差RMSE两个指标,均方根误差主要评价预测模型的整体性能,而最大绝对误差主要衡量预测模型的局部性能,即:
其中,Y为SOC的真实值,Y′为SOC的预测值。
两种工况对应的仿真结果如图3、图4所示。其中的(a)、(b)两图的横坐标为“工况时间/ns”,n为两个工况采样间隔,单位为“s”,由于两个工况的数据总量不同,n的值也不同,每个工况均采样25个点;纵坐标分别为SOC和SOC的估计误差,图例中,REL-SOC为SOC的真实值,RRVM-SOC和IRVM-SOC分别为两种算法的预测值。
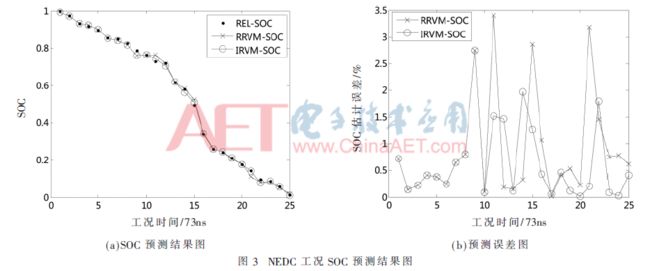

从图3和图4可以看出:在两种工况下,IRVM算法和RRVM算法的预测误差均在5%以内,拟合效果和预测效果都很好。在预测阶段,两种算法的在线训练集均有新的相关向量加入,相比于图2的RVM算法仅用初始训练集直接预测的结果来说,此两种算法均改善了RVM算法多步预测能力差的问题,且受初始训练样本数的影响较小。
为进一步对比不同算法在不同工况下的性能,表1给出了相应的性能数据。其中工况数据列为两种工况以及工况数据的总量;M为相关向量的个数。由表1可以看出:
(1)IRVM算法和RRVM算法的精度对比:在NEDC工况中,RRVM算法的最大误差和均方根误差均大于IRVM算法,在1015工况中则相反。由此可知,在不同的工况下,两种算法的预测精度和稳定性相似,即IRVM算法预测锂电池SOC时没有过多地丢失相关向量,可以保证预测的精度。
(2)IRVM算法和RRVM算法的计算效率对比:在两种工况下,IRVM算法的运行速度均比RRVM算法的运行速度快,相关向量的个数少。这是因为IRVM算法进行预测时,每次只将相关向量而不是所有数据留下来和新增的样本一起进行训练,彻底丢弃了非相关向量,使训练样本大大减小,提高了计算效率。
4 结论
本文提出的IRVM算法将增量学习法与RVM离线算法结合在一起,改善了RVM算法多步预测能力差的问题,提高了预测精度。以锂离子电池SOC在线预测为应用背景,IRVM算法使用快速序列稀疏贝叶斯学习算法进行训练,减小了矩阵运算的复杂度,提高了算法的计算效率。实验分析了核参数、训练样本的大小以及预测步长对算法预测精度的影响,算法中通过自动调整核参数的方式保证算法的预测精度。
基于NEDC和1015典型工况对所提出的IRVM锂离子电池SOC预测方法与RRVM进行分析对比,结果表明,IRVM算法与RRVM算法的预测精度相当,但IRVM算法的计算效率更高,相关向量更稀疏,适用于多种工况的预测。
参考文献
[1] 郑旭,黄鸿,郭汾.动力电池SOC估算复杂方法综述[J].电子技术应用,2018,44(3):3-6,10.
[2] 刘大同,周建宝,郭力萌,等.锂离子电池健康评估和寿命预测综述[J].仪器仪表学报,2015,36(1):1-16.
[3] TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001,1(3):211-244.
[4] WIDODO A,SHIM M C,CAESARENDRA W,et al.Intelligent prognostics for battery health monitoring based on sample entropy[J].Expert Systems with Applications An International Journal,2011,38(9):11763-11769.
[5] 高向阳,张骏,宁宁.基于相关向量机的蓄电池荷电状态预测[J].电源技术,2010,34(12):1273-1275.
[6] TIPPING M E,FAUL A C.Fast marginal likelihood maximisation for sparse Bayesian models[C].Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics,2003:3-6.
[7] SYED N A,LIU H,SUNG K K.Incremental learning with support vector machines[J].Technical Reports,2001,228(4):641-642.
[8] LIU D,ZHOU J,PAN D,et al.Lithium-ion battery remaining useful life estimation with an optimized Relevance Vector Machine algorithm with incremental learning[J].Measurement,2015,63:143-151.
作者信息:
王 超,范兴明,张 鑫,高琳琳,刘华东
(桂林电子科技大学 电气工程及其自动化系,广西 桂林541004)