第十七课.感知机

感知机算法

感知机模型

感知机（perceptron）模型是一个简单的线性二分类模型，它是支持向量机与神经网络的基础。感知机模型的数学表达式如下：
$$f(x)=sign(wx+b)$$
$$w\in R^n,x\in R^n,b\in R$$
对应实现：

import numpy as np

def predict(x,w,b):
    ''' 预测函数
    x: 一维 numpy 数组表示的样本特征向量
    w：一维 numpy 数组表示的权值向量
    b: 偏置项（标量）
    '''
    # 线性回归的预测输出
    z = sum(w*x)+b
    # 感知机的预测输出
    return sign(z)

感知机模型是在线性回归模型的基础上套了一个符号函数sign，符号函数的定义如下：

符号函数如下：

def sign(x):
    '''符号函数
    x: 函数的输入值（标量）
    '''
    return 1 if x>=0 else -1

与以往认识到的模型不同，感知机分类模型的输出值为1和-1，其中 1 代表预测为正例，-1 代表预测为负例；

感知机模型对应特征空间中的一个超平面：$wx+b=0$，这个超平面将特征空间分为两部分，正负样本分别位于超平面的两侧，因此这个超平面又叫做分离超平面。例如，二维特征空间中的分离超平面是这样的：

特征空间中的每个样本点对应该样本的特征向量。其中$[3,3]$和$[4,3]$为正样本，用红色标记；$[1,1]$为负样本，用绿色标记；直线$1.5x_1+x_2-3=0$为二维特征空间中的一个分离超平面，它将正负样本分隔在两侧；

图中的感知机模型表达式为：$sign(1.5x_1+x_2-3)$，它可以完全正确地对图中的样本实现二分类。例如，将负样本 $[1,1]$ 代入 $sign(1.5x_1+x_2-3)$ 得到的结果为 -1；将正样本 $[3,3]$ 代入 $sign(1.5x_1+x_2-3)$ 得到的结果为 +1；

对于给定的数据集 $T$，若存在一个超平面 $S$ 可以将数据集中的正负样本完全正确地划分到超平面的两侧，则称该数据集为线性可分数据集；

但现实世界中有很多数据集是线性不可分的，比如：

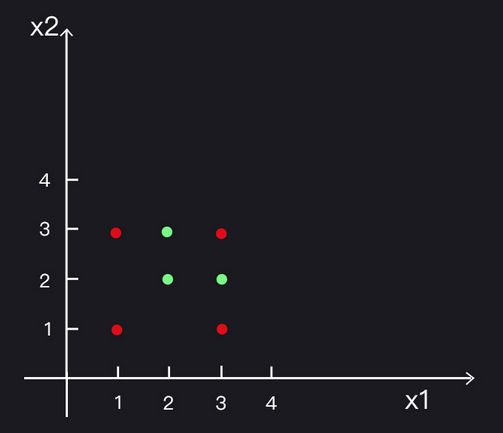
如上图所示，在这样的一个二维特征空间中，无法找到将正负样本完全分开的分离超平面；

损失函数

对于某个样本$(x_i,y_i)$，感知机模型的分类损失为：
$$loss(w,b)=-y_i(w{x}_i+b)$$
假设超平面 $S$ 的样本集合是 $M$，则感知机 $sign(wx+b)$ 学习的损失函数定义为：
$$L(w,b)=-\sum _{x_i\in M}{y}_i(w{x}_i+b)$$

随机梯度下降

感知机模型使用随机梯度下降来进行模型参数的优化，具体做法如下：

• 随机选取一个样本$(x_i,y_i)$，计算模型在该样本点上的损失对模型参数的梯度：
  $$\frac{\partial loss}{\partial w}=-y_i{x}_i,\frac{\partial loss}{\partial b}=-y_i$$
• 利用梯度更新模型参数：
  $$w-=\alpha \frac{\partial loss}{\partial w},b-=\alpha \frac{\partial loss}{\partial b},0<\alpha <1$$

梯度下降法即沿梯度的负方向进行参数更新，$\alpha$表示梯度下降的步长，也叫学习率；

算法流程

• 1.输入训练数据集 $T$，学习率 $\alpha$；
• 2.初始化权值向量 $w$ 和偏置参数 $b$；
• 3.遍历训练集中的样本点 $(x_i,y_i)$；
• 4.若 $y_i(w{x}_i+b)\le 0$（证明是误分类点），则使用如下公式更新模型参数：
  $$w=w+\alpha y_i{x}_i,b=b+\alpha y_i$$
• 5.重复步骤3到4，直到训练集中没有误分类点（相当于损失函数已经达到最小值）；

实现如下：

def fit(X_train,y_train,alpha):
    ''' 模型参数迭代
    X_train: m x n 的 numpy 二维数组
    y_train：有 m 个元素的 numpy 一维数组
    alpha: 学习率
    '''
    # 初始化模型参数
    w = np.random.randn(X_train.shape[1])
    b = np.random.randn() 

    # 使用随机梯度下降进行模型迭代
    while True:
        # 误分类点的个数
        num_errors = 0
        # 遍历训练集中的样本数据
        for x,y in zip(X_train,y_train):
            # 当线性回归的预测值和样本的类别取值异号时
            if y*(sum(w*x)+b) <= 0:
                # 误分类个数加一
                num_errors += 1
                # 使用梯度下降法更新模型参数
                w += alpha * y * x
                b += alpha * y
        # 直到训练集中没有误分类点时，停止迭代
        if num_errors == 0:
            break
    # 返回模型参数    
    return w,b

假设有以下案例：

# 数据
data = np.array([[3,3,1],
                 [4,3,1],
                 [1,1,-1]])
X_train = data[:,:2]
y_train = data[:,-1]

# 训练感知机模型,获取模型参数
w,b = fit(X_train,y_train,alpha=1)
# 样本数据和分离超平面在二维空间的可视化
visualization_2D(X_train,y_train,w,b)

可视化的函数：

import matplotlib.pyplot as plt

# 字体设置
plt.rc('font',family='Times New Roman')

def visualization_2D(X,y,w,b):
    '''样本在二维空间的可视化'''
    # 特征维度必须是二维，否则触发异常
    assert X.shape[1]==2
    # 存放分离超平面的边界点
    data = []
    # 分离超平面边界点的横坐标 x1 的取值
    x1_min = X[:,0].min()-1
    x1_max = X[:,0].max()+1
    # 计算对应的纵坐标 x2 的取值
    for x1 in [x1_min,x1_max]:
    	# w[0]x1+w[1]x2+b=0
        x2 = (x1*w[0]+b)/(-w[1])
        data.append([x1,x2])
    # 将边界点转为 numpy 数组，方便取数
    data = np.array(data)
    # 绘制正样本点，标记为红色
    plt.scatter(X[y==1][:,0],X[y==1][:,1],c='r')
    # 绘制负样本点，标记为绿色
    plt.scatter(X[y==-1][:,0],X[y==-1][:,1],c='g')
    # 绘制分离超平面，标记为蓝色
    plt.plot(data[:,0],data[:,1],c='b')
    # 设置坐标轴名称
    plt.xlabel('x1')
    plt.ylabel('x2')
    # 设置纵坐标显示范围
    plt.ylim(X[:,1].min()-1,X[:,1].max()+1)

    # 网格
    plt.grid(True, linestyle=':', color='r', alpha=0.6)

    # 显示图片
    plt.show()

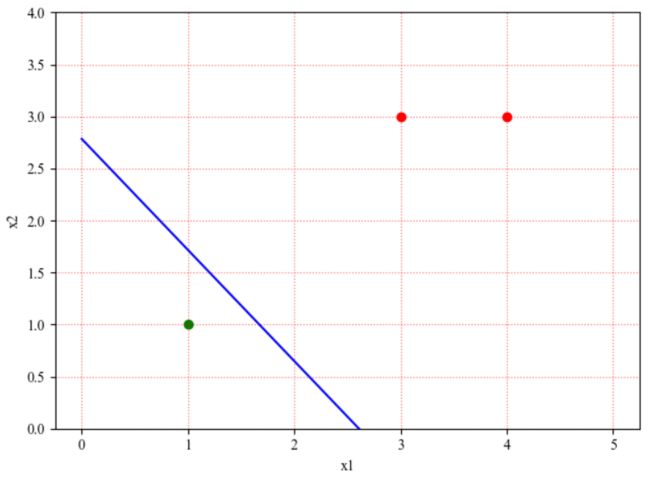
实际上能够找到无数个将正负样本分开的超平面，即感知机模型的解不唯一；

numpy实现感知机

进一步地，在鸢尾花数据集上实现感知机分类算法：

import numpy as np

class Perceptron(object):
    '''感知机算法的实现'''

    def __init__(self, alpha):
        ''' 初始化实例属性
        alpha: 学习率
        '''
        self.alpha = alpha

    def sign(self, x):
        '''符号函数
        x: 函数的输入值（标量）
        '''
        return 1 if x >= 0 else -1

    def predict(self, x):
        ''' 预测函数
        x: 一维数组表示的样本特征向量
        '''
        # 线性回归的预测输出
        z = sum(self.w * x) + self.b
        # 感知机的预测输出
        return self.sign(z)

    def fit(self, X_train, y_train):
        ''' 训练函数
        X_train: m x n 的 numpy 二维数组
        y_train：有 m 个元素的 numpy 一维数组
        '''
        # 初始化模型参数
        self.w = np.random.randn(X_train.shape[1])
        self.b = np.random.randn()

        # 使用随机梯度下降进行模型迭代
        while True:
            # 误分类点的个数
            num_errors = 0
            # 遍历训练集中的样本数据
            for x, y in zip(X_train, y_train):
                # 当线性回归的预测值和样本的类别取值异号时
                if y * (sum(self.w * x) + self.b) <= 0:
                    # 误分类个数加一
                    num_errors += 1
                    # 使用梯度下降法更新模型参数
                    self.w += self.alpha * y * x
                    self.b += self.alpha * y
            # 直到训练集中没有误分类点时，停止迭代
            if num_errors == 0:
                break

        return self


from sklearn.datasets import load_iris

# 载入鸢尾花数据集（线性可分）
X, y = load_iris(return_X_y=True)

# 取前两类的数据（类别标记为0和1）
X = X[y != 2]
y = y[y != 2]
print(X.shape,y.shape) # (100, 4) (100,)

# 将类别标记中的 0 改成 -1，作为负样本
y[y==0]=-1

# 设置学习率为 1，进行模型迭代
model = Perceptron(1).fit(X, y)
# 打印模型参数
print('w =', model.w, 'b =', model.b)
# w = [-1.60349661 -3.35526409  6.64750285  4.827056  ] b = -1.5430050734183185

# 预测新数据
x_new = np.array([3, 4, 1, 5])
y_pred = model.predict(x_new)
print(x_new, y_pred) # [3 4 1 5] 1