计算机图形学-扫描转换圆弧-方程法-中点算法-内多边形逼近算法-OPENGL实现-详解
扫描转换圆弧
- 说明与环境配置
-
- 环境配置
- 扫描转换圆弧
-
- 方法一: 方程法
-
- 代码描述: 算法比较简单, 暂无代码.
- 方法二: 中点算法
-
- 核心代码:
- 方法三: 逼近算法
-
- 核心代码:
- 工程代码下载与效果展示:
说明与环境配置
生成一段圆弧的方法主要有三种:
- 方程法
- 中点算法
- 逼近算法
我所采用的实现方式:
OPENGL1.1库 + VS2019
环境配置
https://blog.csdn.net/BoyInC0de/article/details/90079870
扫描转换圆弧
方法一: 方程法
利用隐函数方程: x 2 + y 2 = R 2 \ x^2+y^2=R^2 x2+y2=R2
( x i , y i ) = R 2 − x i 2 → 取 整 ( x i , y i , r ) \ (x_i,y_i)=\sqrt{R^2-x_i^2} \xrightarrow{取整} (x_i,y_{i,r}) (xi,yi)=R2−xi2取整(xi,yi,r)
离散角度:
利用参数方程:
{ x = R cos θ y = R sin θ \begin{cases} x=R\cos\theta \\ y=R\sin\theta \end{cases} { x=Rcosθy=Rsinθ
( r o u n d ( R cos θ i ) , r o u n d ( R sin θ i ) ) (round(R\cos\theta_i),round(R\sin\theta_i)) (round(Rcosθi),round(Rsinθi))
这种算法的缺点就是:
开平方, 三角函数计算量大
代码描述: 算法比较简单, 暂无代码.
方法二: 中点算法
利用圆弧的正负划分性来绘制圆弧, 说到正负划分性, 可以参考上一篇 直线段的扫描算法中, 中点算法也利用了直线的正负划分性
传送门: https://blog.csdn.net/BoyInC0de/article/details/90549419
方程:
F ( x , y ) = x 2 + y 2 − R 2 = 0 F(x,y)=x^2+y_2-R^2=0 F(x,y)=x2+y2−R2=0
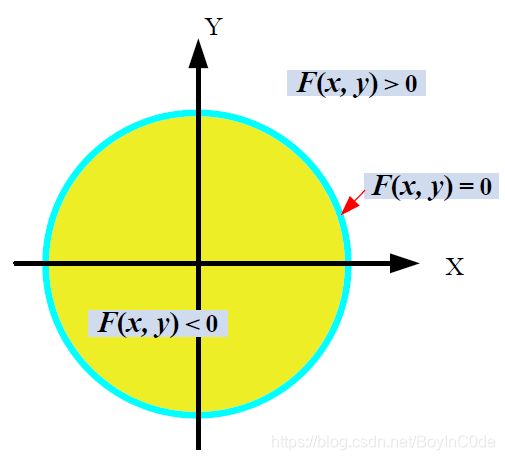
正负划分性:
圆弧外的点: F ( x , y ) > 0 \ F(x,y)\gt0 F(x,y)>0
圆弧内的点: F ( x , y ) < 0 \ F(x,y)\lt0 F(x,y)<0
圆弧上的点: F ( x , y ) = 0 \ F(x,y)=0 F(x,y)=0
圆具有八分对称性:
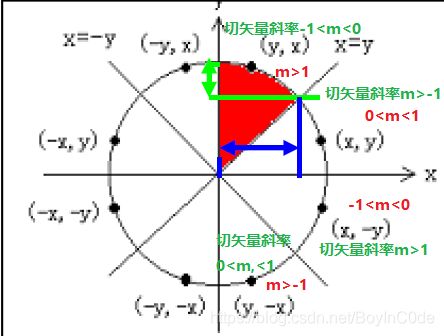
至于为什么八分, 就要从斜率的角度来考虑, 参考上一篇文章, 直线段在绘制时, 也分为了4个斜率
以第一象限切矢量斜率 − 1 < m < 0 \ -1\lt m\lt 0 −1<m<0为例说明:
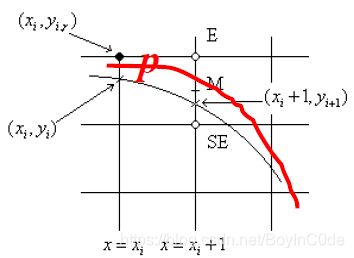
- 如果 F ( M ) ≥ 0 \ F(M)\geq0 F(M)≥0, 中点M在圆内, 取点E
- 如果 F ( M ) < 0 \ F(M)\lt0 F(M)<0, 中点M在圆外, 取点SE
构造判别式:
取第一个点 ( x 0 , y 0 ) \ (x_0,y_0) (x0,y0), 下一点(中点) M ( x 0 + 1 , y 0 − 0.5 ) \ M(x_0+1,y_0-0.5) M(x0+1,y0−0.5)
设 d = F ( M ) = F ( x 0 + 1 , y 0 − 0.5 ) = ( x 0 + 1 ) 2 + ( y 0 − 0.5 ) 2 − R 2 \begin{aligned} 设d=F(M) &=F(x_0+1,y_0 - 0.5)\\ &= (x_0+1)^2 + (y_0 - 0.5)^2 - R^2 \end{aligned} 设d=F(M)=F(x0+1,y0−0.5)=(x0+1)2+(y0−0.5)2−R2
取第三个点分两种情况:
第一种情况上一点的: d ≥ 0 \ d\geq0 d≥0, 取SE:
初始点: ( x 0 , y 0 ) \ (x_0,y_0) (x0,y0) , 第一个点: M ( x 0 + 1 , y 0 − 1 ) \ M(x_0+1,y_0-1) M(x0+1,y0−1), 那么第二个点 ( x 0 + 2 , y 0 − 1.5 ) \ (x_0+2,y_0-1.5) (x0+2,y0−1.5) 代入F(x,y)
F ( x 0 + 2 , y 0 − 1.5 ) = ( x 0 + 2 ) 2 + ( y 0 − 1.5 ) 2 − R 2 = ( x 0 2 + 2 x 0 + 1 ) + ( y 0 2 − y 0 + 0.25 ) − R 2 + 2 x 0 + 3 − 2 y 0 + 2 = d + ( 2 x 0 + 3 ) + ( − 2 y 0 + 2 ) \begin{aligned} F(x_0+2,y_0-1.5) &= (x_0+2)^2 + (y_0 - 1.5)^2 -R^2 \\ &= (x_0^2+2x_0+1)+(y_0^2-y_0+0.25)-R^2+2x_0+3-2y_0+2 \\ &= d +(2x_0+3)+(-2y_0+2) \end{aligned} F(x0+2,y0−1.5)=(x0+2)2+(y0−1.5)2−R2=(x02+2x0+1)+(y02−y0+0.25)−R2+2x0+3−2y0+2=d+(2x0+3)+(−2y0+2)
沿着右下方向, d的增量为 2 ( x 0 − y 0 ) + 5 \ 2(x_0-y_0)+5 2(x0−y0)+5
第二种情况上一点的: d < 0 \ d\lt0 d<0, 取E:
初始点: ( x 0 , y 0 ) \ (x_0,y_0) (x0,y0) , 第一个点: M ( x 0 + 1 , y 0 ) \ M(x_0+1,y_0) M(x0+1,y0), 那么第二个点 ( x 0 + 2 , y 0 − 0.5 ) \ (x_0+2,y_0-0.5) (x0+2,y0−0.5) 代入F(x,y)
F ( x 0 + 2 , y 0 − 0.5 ) = ( x 0 + 2 ) 2 + ( y 0 − 0.5 ) 2 − R 2 = ( x 0 2 + 2 x 0 + 1 ) + ( y 0 2 − y 0 + 0.25 ) − R 2 + 2 x 0 + 3 = d + ( 2 x 0 + 3 ) \begin{aligned} F(x_0+2,y_0-0.5) &= (x_0+2)^2 + (y_0 - 0.5)^2 -R^2 \\ &= (x_0^2+2x_0+1)+(y_0^2-y_0+0.25)-R^2+2x_0+3 \\ &= d +(2x_0+3) \end{aligned} F(x0+2,y0−0.5)=(x0+2)2+(y0−0.5)2−R2=(x02+2x0+1)+(y02−y0+0.25)−R2+2x0+3=d+(2x0+3)
沿着右下方向, d的增量为 2 x 0 + 3 \ 2x_0+3 2x0+3
d的初始值在第一个像素 ( 0 , R ) \ (0,R) (0,R)处
d 0 = F ( 1 , R − 0.5 ) = 1.25 − R d_0 = F(1,R-0.5) = 1.25-R d0=F(1,R−0.5)=1.25−R
因为算法中有浮点数, 和直线段中的做法类似, 我们用 h = 4 d \ h=4d h=4d, 得到:
H 0 = 5 − 4 R H_0=5-4R H0=5−4R
通过归纳法, 我们就得到递推公式:
H 0 = 5 − 4 R H i + 1 = { H i + 8 x i + 12 , H i ≤ 0 H i + 8 ( x i − y i ) + 20 , H i > 0 y i + 1 = { y i , H i ≤ 0 y i − 1 , H i > 0 x i + 1 = x i + 1 \begin{aligned} H_0 &= 5-4R \\ H_{i+1}&= \begin{cases} H_i + 8x_i + 12, & \text{$H_i\leq 0$} \\ H_i + 8(x_i-y_i)+20, & \text{$H_i\gt 0$} \\ \end{cases}\\ y_{i+1}&= \begin{cases} y_i, \quad\quad &\text{$H_i\leq 0$} \\ y_i-1, \quad\quad & \text{$H_i\gt 0$} \\ \end{cases}\quad\quad\quad x_{i+1} = x_i+1 \end{aligned} H0Hi+1yi+1=5−4R={ Hi+8xi+12,Hi+8(xi−yi)+20,Hi≤0Hi>0={ yi,yi−1,Hi≤0Hi>0xi+1=xi+1
为了便于程序实现:
令
E i = 8 x i + 12 E_i = 8x_i + 12 Ei=8xi+12
S E i = 8 ( x i − y i ) + 20 SE_i=8(x_i-y_i)+20 SEi=8(xi−yi)+20
递推公式:
E i + 1 = 8 ( x i + 1 ) + 12 = 8 x i + 12 + 8 = E i + 8 S E i + 1 = 8 ( x i + 1 − y i + 1 ) + 20 = { S E i + 8 , H i ≤ 0 S E i + 16 , H i > 0 \begin{aligned} E_{i+1} &= 8(x_i+1) +12 \\ &=8x_i+12+8 \\ &=E_i + 8 \\ SE_{i+1} &= 8(x_{i+1}-y_{i+1})+20 \\ &= \begin{cases} SE_i + 8, & \text{$H_i \leq 0$} \\ SE_i + 16, & \text{$H_i \gt 0$} \\ \end{cases} \end{aligned} Ei+1SEi+1=8(xi+1)+12=8xi+12+8=Ei+8=8(xi+1−yi+1)+20={ SEi+8,SEi+16,Hi≤0Hi>0
初始值:
E 0 = 8 x i + 12 = 12 S E 0 = 8 ( x i − y i ) + 20 = 20 − 8 R \begin{aligned} E_0 &= 8x_i+12=12 \\ SE_0 &= 8(x_i-y_i)+20=20-8R \end{aligned} E0SE0=8xi+12=12=8(xi−yi)+20=20−8R
为此, 可得到变量关系:
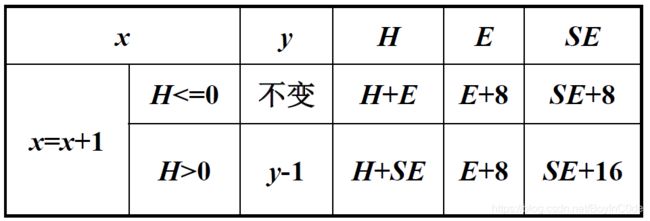
核心代码:
for (i = x0; i < x0 + (int)R * 0.707; i++) { //x0, y0 是圆心, x, y是缓冲区内写的点
if (h > 0) {
--y;
h += se;
e += 8;
se += 16;
}
else {
h += e;
e += 8;
se += 8;
}
x++;
}
方法三: 逼近算法

则逼近边数 n \ n n, 每一边对应圆心角 α \alpha α
假设半径 R = 1 \ R=1 R=1, 初始点 ( x 0 , y 0 ) = ( cos α , sin α ) \ (x_0,y_0)=(\cos\alpha, \sin\alpha) (x0,y0)=(cosα,sinα)
( x 1 y 1 ) = ( s i n ( 2 α ) c o s ( 2 α ) ) = ( cos α − sin α sin α cos α ) ( c o s α s i n α ) = ( cos α − sin α sin α cos α ) ( x 0 y 0 ) \begin{aligned} \begin{pmatrix} x_1\\ y_1\\ \end{pmatrix} = \begin{pmatrix} sin(2\alpha)\\ cos(2\alpha)\\ \end{pmatrix} &= \begin{pmatrix} \cos\alpha&-\sin\alpha\\ \sin\alpha&\cos\alpha\\ \end{pmatrix} \begin{pmatrix} cos\alpha\\ sin\alpha\\ \end{pmatrix} \\ &=\begin{pmatrix} \cos\alpha &-\sin\alpha\\ \sin\alpha&\cos\alpha\\ \end{pmatrix} \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix} \\ \end{aligned} (x1y1)=(sin(2α)cos(2α))=(cosαsinα−sinαcosα)(cosαsinα)=(cosαsinα−sinαcosα)(x0y0)
经过归纳法:
( x i + 1 y i + 1 ) = ( cos α − sin α sin α cos α ) ( x i y i ) \begin{aligned} \begin{pmatrix} x_{i+1}\\ y_{i+1}\\ \end{pmatrix} = \begin{pmatrix} \cos\alpha&-\sin\alpha\\ \sin\alpha&\cos\alpha\\ \end{pmatrix} \begin{pmatrix} x_i\\ y_i\\ \end{pmatrix} \\ \end{aligned} (xi+1yi+1)=(cosαsinα−sinαcosα)(xiyi)
特点:
α \alpha α是常数, sin α \sin\alpha sinα, cos α \cos\alpha cosα 只需要在开始时计算一次.
所以一个顶点只需4次乘法, 共 4 n \ 4n 4n次乘法, 外加直线段的中点算法的计算量.
(我上传的代码里是6n次乘法, 已经将改正写在后面)
核心代码:
for (int i = 0; i <= edgen; i++) {
glVertex2f(x0 + R * x, y_0 + R * y);
temp = x;
x = ca * x - sa * y;
y = sa * temp + ca * y;
}
工程代码下载与效果展示:
该代码采用包含圆弧绘制的两种算法:
**中点算法, 和 内多边形逼近算法. **
分别采用函数来绘制, 可自选中点算法或内多边形逼近算法, 可调节内多边形边数, 可调节颜色
虽然OpenGL1.1库文件较老, 但不论是对于教学还是实践, 对理解直线段算法都具有重要意义.
下载地址: https://download.csdn.net/download/boyinc0de/11209226
更正:
下载后第78行改为:
x = R * ca; y = R * sa;
第80行改为:
glVertex2f(x0 + x, y_0 + y);
算法将少做乘法 2 n \ 2n 2n次 !!!
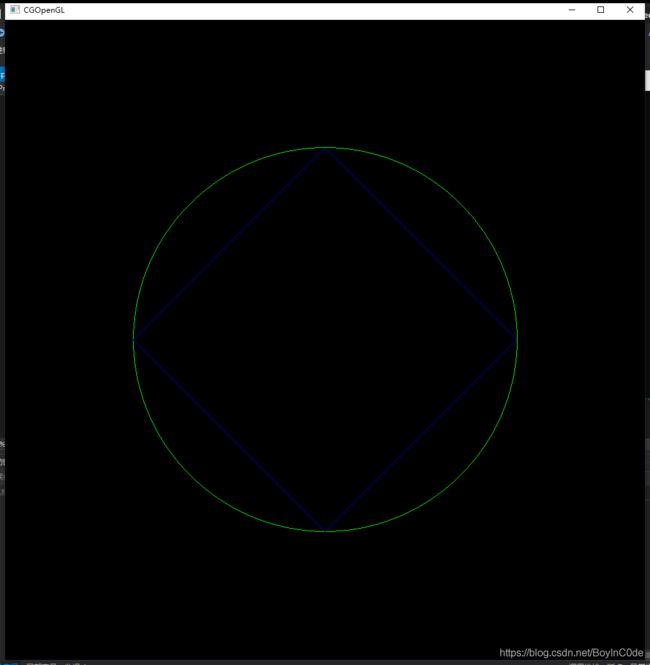
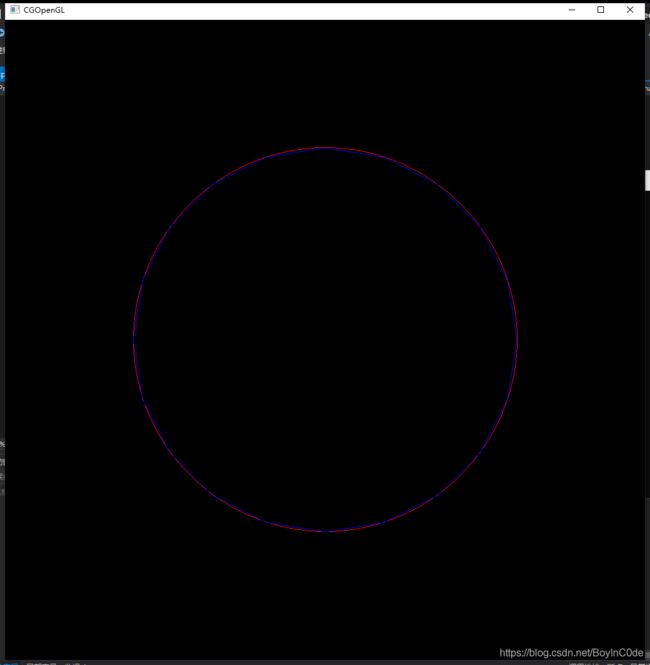
效果展示:
其中外侧图形为: 中点算法
内侧图形为: 逼近算法