排序

关于排序的算法，算是基础知识了，排序的算法有很多，这里总结一些常见的算法：冒泡排序、选择排序、插入排序、快速排序、桶排序、shell排序、归并排序等。

冒泡排序

主要思想是依次比较两个相邻的数字的大小，将小的放在前面，大的放在后面，由第一个元素开始，直到最后一个，重复上诉过程最多n次，就可以将数据排好顺序。冒泡排序法是稳定的，时间复杂度为O(n^2)。
代码实现上，冒泡排序由于理解起来比较简单，所以代码也很清晰。

void Solution::BubbleSort(std::vector<int> &arr)
{
    int i, j;
    for (i = 0; i < arr.size() - 1; i++)
    {
        for (j = arr.size() - 1; j > i; j--)
        {
            if (arr[j-1] > arr[j])
            {
                swap(arr, j-1, j);+
            }
            else
            {
                continue;
            }
        }
    }
}

冒泡排序是一种比较排序法。

选择排序

选择排序的主要思想是先从n-k个元素中找到最小的那个，将其放在已经排好序的k个数字的后面，其时间复杂度也是O(n^2)。选择排序法应该是最容易理解的一种排序方法

void Solution::ChoiceSort(std::vector<int> &arr)
{
    //
    int i, j;
    for (i = 0; i < arr.size() - 1; i++)
    {
        for (j = i + 1; j < arr.size(); j++)
        {
            //
            if (arr[i]>arr[j])
            {
                swap(arr, i, j);
            }
            else
            {
                continue;
            }
        }
    }
}

选择排序法也是一种比较排序法。

插入排序

插入排序的主要思想是从表中选取第一个元素，然后插入有序表中合适位置，使有序表依然有序。插入排序分为直接插入排序和折半插入排序。直接插入排序算法是稳定的，时间复杂度为O(n^2)。
算法的过程：待排序数列arr有n个元素，则需要n-1次插入。选中间一个时刻，即第k次插入，则已经有arr的前k个元素已经完成了排序，不妨令这个排好的序列为B，存在一个list（为了方便插入）里面。通过将arr[k]和B中元素依次比较，找到合适的位置插入，即完成该次插入。

void Solution::InserSort(std::vector<int> &arr)
{
    int n = arr.size();
    if (n <= 1)
        return;
    //std::shared_ptr sp(new int[n]);
    int *p_val = new int[n];
    p_val[0] = arr[0];
    for (int k = 1; k < n; k++)
    {
        int i = k - 1;
        p_val[i + 1] = arr[k];
        while (i >= 0)
        {
            if (p_val[i]>arr[k])
            {
                p_val[i + 1] = p_val[i];
                p_val[i] = arr[k];
                i--;
            }
            else
            {
                //
                break;
            }
        }
    }
    //
    for (int i = 0; i < n; i++)
    {
        arr[i] = p_val[i];
    }
    delete[]p_val;
}

如果提到优化，则是在插入的时候由于是对于已经排好序的序列进行的插入，所以，可以使用二分法查找插入的位置。不过时间复杂度仍然没有提高多少依然是O(n^2)。

快速排序

快速排序的中心思想概括起来就是选择一个数（我们称之为基准），把他放到数据中他应该在为位置（正确的顺序的位置）。那么如何使得这个数被放在他在数组中正确的位置呢？记这个数字为key，设想一下这个数组排序后的结果，对于key来说，必然是左边的都小于等于key，key右边的都大于等于key。现在我们就根据这个套路给key确定位置。
先选一个key然后将所有比key小的值放在key的左边，其余放在右侧，然后分别再对两侧进行排序，得到最后的结果。
实现代码如下：

void Solution::QuickSort(std::vector<int> &arr, int left, int right)
{
    //快速排序
    int i = left + 1;
    int j = right;
    //int key = left;
    if (left > right)
        return;
    while (i < j)
    {
        while (arr[j] > arr[left] && iwhile (arr[i] < arr[left] && iif (i < j)
        {
            swap(arr, i, j);
        }   
    }
    swap(arr, left, j);
    QuickSort(arr, left, j - 1);
    QuickSort(arr, j + 1, right);
}

快速排序的消耗的时间主要是在区域的划分上。实现思路就是先选一个基准点，例如，选择区间最左侧作为基准点，然后先从右开始寻找第一个小于基准点的值，找到以后，再从左开始找第一个大于基准点的值，找到以后，互换两个位置上的元素。当一轮结束以后，将基准点和最后停止的位置互换，这样就排好了基准点的位置，然后两侧的数值在分组进行快速排序。

计数排序

计数排序是基数排序的基础，基本思想是：对每一个元素x，确定小于x的元素个数，就可以把x直接放到它在有序序列的位置上。
过程描述：假设在待排序序列arr中值的范围是[0,k]，其中k为待排序元素序列中的最大值。首先用一个辅助数组count记录各个值出现在arr中的次数，比如count[i]表示i在arr中的个数，然后一次改变count中元素的值，使count[i]表示a中不大于i的元素个数。然后从后往前扫描arr序列，arr中的元素根据count中的信息直接放到辅助数组b中，然后把有序序列b复制到arr中。

基数排序

在计数排序中，当k很大时，时间和空间的开销都会增大（可以想一下对序列{8888,1234,9999}用计数排序，此时不但浪费很多空间，而且时间方面还不如比较排序）。于是可以把待排序记录分解成个位(第一位)、十位(第二位)….然后分别以第一位、第二位…对整个序列进行计数排序。这样的话分解出来的每一位不超过9，即用计数排序序列中最大值是9.

桶排序

桶排序（BucketSort）或所谓的箱排序，是一种排序算法，工作原理是将数值分到有限数量的桶子里，然后对每个桶进行排序。
桶排序算法的主要思想：待排序数组A[1…n]内的元素是随机分布，然后将元素划分到各个桶里面

shell排序

又称为希尔排序，是插入排序的进化版，可以说是分组插入排序，算法的过程就是我们先找一个d，作为分组间隔，然后每相差d坐标的元素为一组，则可以分成d组元素，那么，先对每个组进行插入排序，当每个组排序完成以后，再减小d，再次分组，进行分组排序，直到d减到1的时候。
由于通过在进行后面的插入排序时，会发现，好多的数据已经排好顺序的了，所以时间复杂度会降低，因而shell排序的时间复杂度是O(nlogn)。

归并排序

归并排序其实是利用了分治的思想，我们假设先将需要排序的数组arr，分成左右两个部分，分别排序完成后，再合成一个完整的序列，很有意思的是，我们可以依次递归下去，知道不能够再划分。
首先我们假设arr和brr是两个有序的序列，那么如何将两个有序的序列合并称为一个新的有序的数列呢？代码很简单，如下所示：

void inline Solution::MergingArray(std::vector<int> &arr, std::vector<int> &brr, std::vector<int> &ret)
{
    //获取两个需要合并的数列的长度
    int alen = arr.size();
    int blen = brr.size();
    //
    int i(0), j(0), k(0);
    while (iif (arr[i] < brr[j])
        {
            ret.push_back(arr[i++]);
        }
        else
        {
            ret.push_back(brr[j++]);
        }
        while (iwhile (j

上面已经解决了如何将两个有序的数列合并成一个新的有序的数列，再回过头来看归并排序的思想。归并排序的思想就是将待排序的数列一分为二，然后分别对两侧数据排序，如果两侧数据有序，则将两侧数据合并成新的有序数列，过程就是这么简单。
下面是简单的实现过程：

void inline Solution::_Merge(std::vector<int> &arr, int start, int mid, int end)
{
    //函数的作用是将mid两侧的序列合并成新的有序序列
    int i = start, j = mid + 1;
    int alen = mid;
    int blen = end;
    std::vector<int> tmp;
    while (i <= alen&&j <= blen)
    {
        //
        if (arr[i] < arr[j])
        {
            tmp.push_back(arr[i++]);
        }
        else
        {
            tmp.push_back(arr[j++]);
        }
    }
    while (i <= alen)
    {
        tmp.push_back(arr[i++]);
    }
    while (j <= blen)
    {
        tmp.push_back(arr[j++]);
    }
    //数据复制
    for (int i = 0; i < tmp.size(); i++)
    {
        arr[i + start] = tmp[i];
    }
    tmp.clear();
}
void inline Solution::DivideArray(std::vector<int> &arr, int start, int end)
{
    if (start < end)
    {
        int mid = (start + end) / 2;
        //以mid为中心将arr划分成两个序列
        DivideArray(arr, start, mid);       //左边有序
        DivideArray(arr, mid + 1, end);     //右边有序
        _Merge(arr, start, mid, end);       //合并
    }
}

然后就是主函数的实现了，实现就是很简单的事了：

void Solution::MergeSort(std::vector<int> &arr)
{
    //归并排序
    int n = arr.size() - 1;
    DivideArray(arr, 0, n);
}

归并排序是一个比较高效的排序方式，如果只是考虑排序的时间复杂度的话：
设数列长度为N，将数列分成小数列总共需要logN步，而将有序的小序列合并成大序列总共需要N步，故合并的时间复杂度记为O(N)，故整个归并排序的时间复杂度可以记为O(N*longN)。

堆排序

堆排序和快速排序、归并排序都是时间复杂度为O(N*logN)的几种常见的排序方法。
在正式说明堆排序之前，首先简单说明一下数据结构中的二叉堆，二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足两个条件：
1、父节点的键值总是大于或者等于/小于或者等于任何一个子节点的键值，如何设定取决会死最大堆还是最小堆。
2、每个节点的的左子树和右子树都是一个二叉堆，性质和整个二叉堆的性质相同，同为最大堆或者最小堆。
这里，当父节点的键值总是大于或者等于任何子节点的键值时，我们称之为最大堆；当父节点的键值总是小于或者等于任何子节点的键值的时候，我们称之为最小堆。此外还有二项式堆、斐波那契堆等，但是用的较少，一般将二叉堆称之为堆。在下面以最小堆为例来进行讲解。
一般可以用数组来表示堆，i节点的父节点的下标为(i-1)/2，他的左右子节点的下标分别为2*i+1，2*i+2。例如第0节点的左右子节点的下标分别为1和2：

右边是这个最小堆的数组储存方式。
下面是插入最小堆的流程：

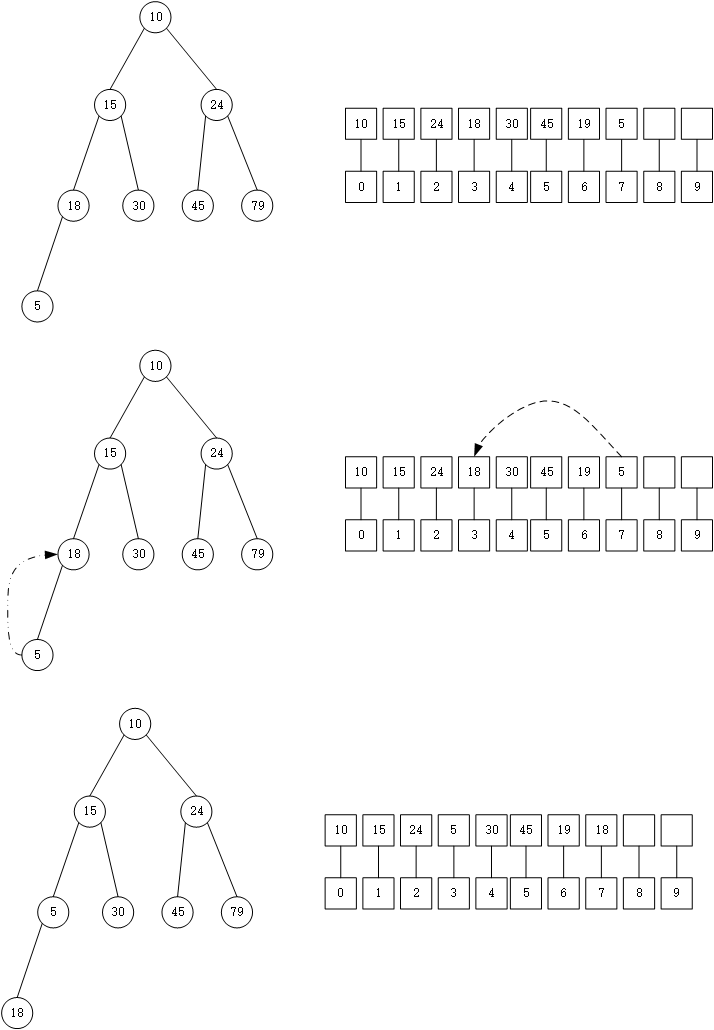
然后依次进行上面的步骤，最后的效果是：

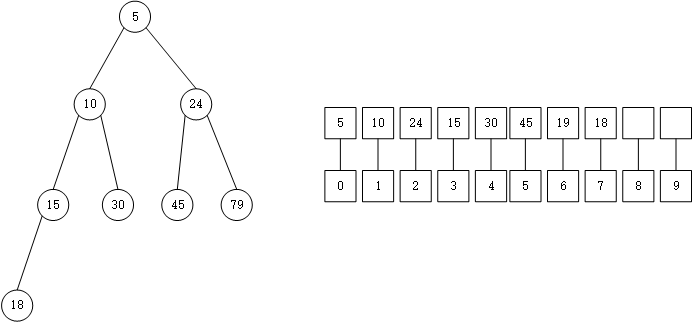
到这里就完成了这次插入。可见，每次插入都是把将要插入的数据放在堆的最后，然后进行一次排序。初始化和插入的过程没有什么区别。我们将上面完成插入操作中进行上向上排序称之为shiftup操作，也就是将i点以及i点的父节点进行排序，使之符合最小堆的形式。此外还有一个操作，将之命名为shiftdown，也就从i节点向子节点从新排序，使之符合最小堆。
删除的时候，总是从堆顶开始删除，不难发现，如果[0,n]为堆，那么[0,n-1]也为堆，所以删除的时候一般是将堆的最后一个元素移动到堆顶覆盖，然后使用shiftdown进行整理，保证最小堆。
然后进入正题，开始进入堆排序，首先可以看到堆建立之后堆顶元素是堆中最小的元素，取出这个元素，再执行下堆的删除操作，这样剩下的元素中最小的元素又到了堆顶的位置，就可以继续上面的操作，直到只有一个元素的，直接取出。
首先构建最小堆的代码，主要是Shiftup和Shiftdown这两个函数：

bool inline Solution::MiniHeapShiftdown(std::vector<int> &heap, int i)
{
    //
    int n = heap.size() - 1;        //获取堆的大小
    int m = 2 * i + 1;
    if (m > n)
        return true;
    if (m + 1 <= n)
    {
        if (heap[m] > heap[m + 1])
        {
            m = m + 1;
        }
    }
    if (heap[i] <= heap[m])
        return true;
    else
    {
        swap(heap, i, m);
        return MiniHeapShiftdown(heap, m);
    }
}
bool inline Solution::MinHeapShiftup(std::vector<int> &heap, int i)
{
    //向上调整顺序
    if (i == 0)
    {
        return true;
    }
    int m = (i - 1) / 2;
    if (heap[m] <= heap[i])
    {
        return true;
    }
    else
    {
        swap(heap, m, i);
        return MinHeapShiftup(heap, m);
    }
}

然后根据上面操作设计入堆操作和出堆操作：

int inline Solution::MinHeapInsert(std::vector<int> &heap, int key)
{
    heap.push_back(key);
    int m = heap.size() - 1;
    if (m == 0)
    {
        return 1;
    }
    MinHeapShiftup(heap, m);
    return 0;
}
int inline Solution::MinHeapPop(std::vector<int> &heap)
{
    //出堆
    if (heap.size() == 1)
    {
        return heap.back();
    }
    int ret = heap[0];
    heap[0] = heap.back();
    heap.pop_back();
    MiniHeapShiftdown(heap, 0);
    return ret;
}

那么堆排序的函数很快就能得到：

void Solution::HeapSort(std::vector<int> &arr)
{
    //堆排序
    std::vector<int> heap;
    for (int i : arr)
    {
        MinHeapInsert(heap, i);
    }
    int len = arr.size();               //length of arr
    for (int i = 0; i < len; i++)
    {
        arr[i] = MinHeapPop(heap);
    }
}

堆排序主要是经历N次入堆操作和N次出堆操作。
接下来是稳定性的分析，稍后上传……