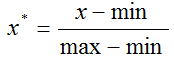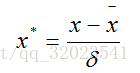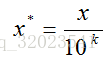python 数据挖掘(6)-- 数据标准化 和 离散化
标准化
数据规划化处理是数据挖掘的一项基础工作,为了消除指标之间的量纲和取值范围差异的影响。
(1)最小 - 最大规范化 将数据映射到 [min,max]
(2)零-均值规划化 将数据处理成均值为 0 ,标准差为 1
(3)小数定标规划化
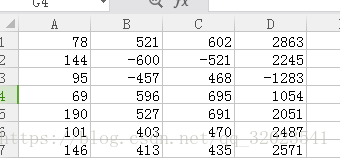
处理 normalization_data.xls 数据规范化如下
#-*- coding:utf-8 -*-
import pandas as pd
import numpy as np
# 数据规范化
datafile = 'wajue/normalization_data.xls'
data = pd.read_excel(datafile,header = None)
# 最大最小规范化
(data - data.min()) / (data.max() - data.min())
# 零-均值规范化
(data - data.mean())/ data.std()
# 小数定标规范化
data/10**np.ceil(np.log10(data.abs().max()))连续属性离散化
一些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。这样,常常需要将连续属性变换成分类属性,即连续属性离散化。常用的离散化有三种方法。
(1)等宽法
将属性的值域分成具有相同宽度的区间,区间的个数由数据本身的特点决定,这种做法的缺点是对离群点敏感,倾向于不均匀的把属性值分布到各个区间。
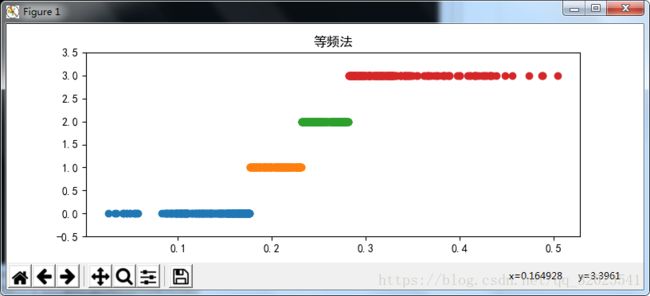
(2)等频法
将相同数量的记录放进每个区间。这种做法虽然避免了属性值分布不均匀的问题,但是可能将相同的数据值分到不同的区间以满足每个区间中固定的数据个数。
(3)聚类法
首先将连续的属性值用聚类算法进行聚类,然后对聚类得到的簇进行处理,合并到一个簇的连续属性值并做同一标记。需要用户指定簇的个数。k-means 需要。
对肝气郁结证型系数 discretization_data.xls 属性离散化处理如下:
#-*- coding:utf-8 -*-
import pandas as pd
import numpy as np
datafile = 'wajue/discretization_data.xls'
data = pd.read_excel(datafile)
data = data[u"肝气郁结证型系数"].copy()
# 离散化数
k = 4
# 等宽法离散化, 各个类比依次命名为0,1,2,3
''' 注意 d 就是由位置和 0,1,2,3 组成的序列 '''
d1 = pd.cut(data, k, labels = range(k))
# 等频法离散化
w = [1.0*i/k for i in range(k+1)]
# 使用 describe 函数自动计算分位数,可以用 w 计算自定义分位数
# w 就是 0, 1/k, 2/k...1 分位数
w = data.describe(percentiles = w)[4:4+k+1]
w[0] = w[0]*(1-1e-10)
d2 = pd.cut(data, w, labels = range(k))
'''
# 聚类分析
from sklearn.cluster import KMeans
# 建立模型,指定聚类数 k
kmodel = KMeans(n_clusters = k,n_jobs = 4)
# 训练模型
kmodel.fit(data.reshape((len(data),1)))
# 输出聚类中心,并且排序
c = pd.DataFrame(kmodel.cluster_centers_).sort(0)
# 以相邻两项中点为边界点
w = pd.rolling_mean(c,2).iloc[1:]
# 加上首末边界点
w = [0] + list(w) + [data.max()]
d3 = pd.cut(data, w, labels = range(k))
'''
def cluster_plot(d,k,s):
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize = (8,3))
plt.title(s)
for j in range(k):
plt.plot(data[d==j],[j for j in d[d==j]],'o')
# 限制 y 轴数据大小
plt.ylim(-0.5,k-0.5)
return plt
cluster_plot(d1,k,u"等宽法").show()
cluster_plot(d2,k,u"等频法").show()