《scikit-learn》PCA（一）

特征选择是从已经存在的特征中选择相关性，信息量最多的特征。
特征创造，比如降维，降维之后，新的特征矩阵就不是任何一个特征了。二十通过线性变换后创造的新的特征，新的特征不再具有可读性。

至于降维的一些算法和数学，在最早的一些文章中已经粗略学习过了。下面我们直接学习如何在scikit-learn中使用它，scikit-learn中有很多种类。

1：主要成分分析：
decomposition.PCA 主要成分分析
decomposition.IncrementalPCA 增量主要成分分析
decomposition.MiniBatchSparePCA 小批量稀疏主要成分分析
decomposition.KernelPCA 核主要成分分析
decomposition.SparePCA 系数主要成分分析
decomposition.TruncateSVD 截断的SVD

2：因子分析
decomposition.FactorAnalysis 因子分析

3：字典学习
decomposition.DictionaryLearning 字典学习

4：高级矩阵分析
Decomposition.LatentDirichletAllocation LDA
decomposition.NMF 非负矩阵分解

下面我们选择几个最基础且常用的，我们呢一起来试试PCA这个。

一：PCA使用和可视化
重要参数是n_components，也就是降维后需要保留的参数，这个参数不能太大或者太小。

先来试一试降到二维的样子

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import pandas as pd

# ======== 第一步：准备数据
iris = load_iris()
print(iris.data.shape)
print(iris.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', iris.target_names)  # 三种分类

# print(pd.DataFrame(iris.data))  # 四个特征，所以就是4维数据，我们无法用图示表示出来，只能用表格打印了

# ======== 第二步：降维操作
pca = PCA(n_components=2)  # 实例化，先降到2维
pca = pca.fit(iris.data)   # 拟合数据
x_dr = pca.transform(iris.data)   # 获取降维后的数据咯

print(pd.DataFrame(x_dr).head())

# y也可以一步到位
# x_dr = PCA(n_components=3).fit_transform(iris.data)

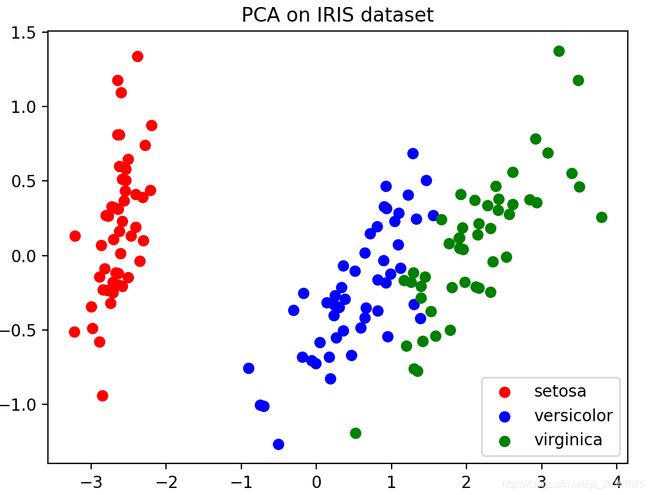
# ======== 第三步：可视化操作
# 按照不同的类别，使用布尔索引来获得不同类别的数据，不同类别的数据用不同的颜色来标注。
# 降维后是俩特征，每个特征作为一个维度，画在二维坐标系上。
colors = ['red', 'blue', 'green']
plt.figure()  # 准备一个画布
for i in range(3):  # 取值0，1，2
    plt.scatter(x=x_dr[iris.target == i, 0], y=x_dr[iris.target == i, 1], c=colors[i], label=iris.target_names[i])
plt.legend()
plt.title('PCA on IRIS dataset')
plt.show()

再来看看降到三维的样子

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import pandas as pd

# ======== 第一步：准备数据
iris = load_iris()
print(iris.data.shape)
print(iris.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', iris.target_names)  # 三种分类

# print(pd.DataFrame(iris.data))  # 四个特征，所以就是4维数据，我们无法用图示表示出来，只能用表格打印了


# ======== 第二步：降维操作
x_dr = PCA(n_components=3).fit_transform(iris.data)

# ======== 第三步：可视化操作
# 按照不同的类别，使用布尔索引来获得不同类别的数据，不同类别的数据用不同的颜色来标注。
# 降维后是俩特征，每个特征作为一个维度，画在二维坐标系上。

from mpl_toolkits.mplot3d import Axes3D  # 空间三维画图

colors = ['red', 'blue', 'green']

fig = plt.figure()  # 准备一个画布
ax = Axes3D(fig)
for i in range(3):  # 取值0，1，2
    ax.scatter(xs=x_dr[iris.target == i, 0], ys=x_dr[iris.target == i, 1], zs=x_dr[iris.target == i, 2], c=colors[i],
                label=iris.target_names[i])
ax.legend()
ax.set_zlabel('Z', fontdict={
     'size': 10, 'color': colors[2]})
ax.set_ylabel('Y', fontdict={
     'size': 10, 'color': colors[1]})
ax.set_xlabel('X', fontdict={
     'size': 10, 'color': colors[0]})
plt.title('PCA on IRIS dataset')
plt.show()

可以看出来哈，每一个类别的数据整体是分布相对有自己的空间分布位置的。
因此，有了这个明显的特点我们才能去做区分。这个数据集发现是很简单很简单的了，随便一个常见的机器学习模型都能做得很好的了。

二：n_components的选择

除此之外还可以得到降维后的一些信息
print(pca.explained_variance_) # 可以查看每个新的特征上的方差，方差越大，所带的信息量越大。
print(pca.explained_variance_ratio_) # 查看降维后，每个新特征所占的信息量占原始数据信息量的百分比。
print(pca.explained_variance_ratio_.sum()) # 看看信息损失多少？特征砍掉了，信息丢失多少呢？

上面的累计可解释方差的贡献率，可以作为选择n_components的评估指标，能帮我们选择出一个好的n_components参数。原因是之前学习过，按照SVD分解或者矩阵分解后，前面几个大奇异值或者特征值会占据几乎全部的信息量。

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np

# ======== 第一步：准备数据
iris = load_iris()
print(iris.data.shape)
print(iris.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', iris.target_names)  # 三种分类

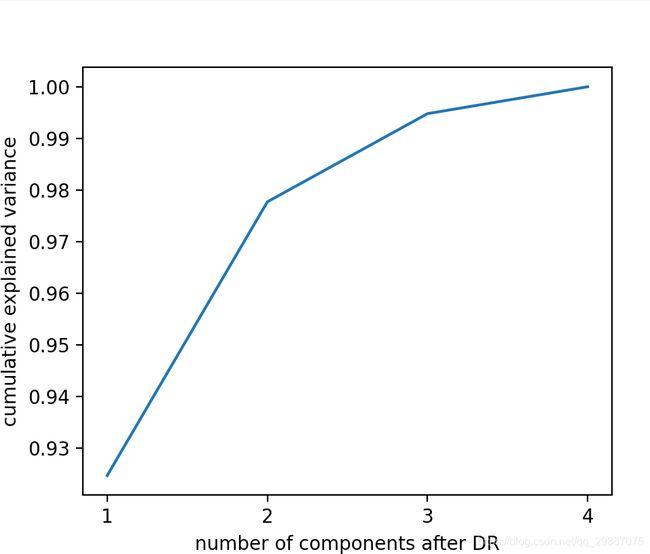
pca_line = PCA().fit(iris.data)  # 什么参数都不写，代表是 min(x.shape)，一般情况下就是原特征数目了。
print(pca_line.explained_variance_ratio_)
cumsum = np.cumsum(pca_line.explained_variance_ratio_)  # 使用累计统计，来表示可解释特征的信息占比和
print(cumsum)

plt.plot(range(1, iris.data.shape[1] + 1), cumsum)
plt.xticks(range(1, iris.data.shape[1] + 1))  # 横坐标轴是整数
plt.xlabel('number of components after DR')
plt.ylabel('cumulative explained variance')
plt.show()

如下图：

换个例子展示：

from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np

# ======== 第一步：准备数据
data = load_breast_cancer()
print(data.data.shape)
print(data.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', data.target_names)  # 三种分类

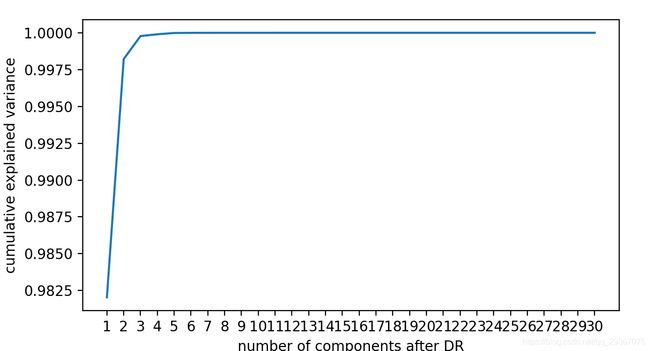
pca_line = PCA().fit(data.data)  # 什么参数都不写，代表是 min(x.shape)，一般情况下就是原特征数目了。
print(pca_line.explained_variance_ratio_)
cumsum = np.cumsum(pca_line.explained_variance_ratio_)  # 使用累计统计，来表示可解释特征的信息占比和
print(cumsum)

plt.plot(range(1, data.data.shape[1] + 1), cumsum)
plt.xticks(range(1, data.data.shape[1] + 1))  # 横坐标轴是整数
plt.xlabel('number of components after DR')
plt.ylabel('cumulative explained variance')
plt.show()

看来这个数据可以压缩到很低啊。
一般我们选择转折点的对应的特征数目。

上面讲的是我们自己来选择超参数。
如果我们不想自己选择，那么我们还可以让算法帮我自己选择，比如使用最大似然估计来自动帮我选择一个好的n_components。

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np

# ======== 第一步：准备数据
iris = load_iris()
print(iris.data.shape)
print(iris.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', iris.target_names)  # 三种分类

# ======== 第一步：使用pca
pca_mle = PCA(n_components='mle').fit(iris.data)  # 输入mle，就表示让算法自动帮我们使用最大似然估计来选择一个好的特征数目。
print(pca_mle.explained_variance_ratio_)
cumsum = np.cumsum(pca_mle.explained_variance_ratio_.sum())  # 使用累计统计，来表示可解释特征的信息占比和
print(cumsum)

data_dr = pca_mle.transform(iris.data)
print(data_dr.shape)

我们还可以使用按找信息量占比来选择。
输入浮点数[0,1]之间的，并且让参数svd_solver=’full’。表示希望降维后，总的可解释性方差信息量占比是保留多少。

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import numpy as np

# ======== 第一步：准备数据
iris = load_iris()
print(iris.data.shape)
print(iris.target.shape)  # iris.target的值是：0、1、2
print('所有的种类是：', iris.target_names)  # 三种分类

# ======== 第一步：使用pca
pca_mle = PCA(n_components=0.97,svd_solver='full').fit(iris.data)  # 输入mle，就表示让算法自动帮我们使用最大似然估计来选择一个好的特征数目。
print(pca_mle.explained_variance_ratio_)
cumsum = np.cumsum(pca_mle.explained_variance_ratio_)  # 使用累计统计，来表示可解释特征的信息占比和
print(cumsum)

data_dr = pca_mle.transform(iris.data)
print(data_dr.shape)