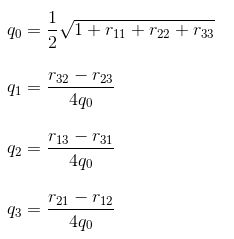05轨迹规划基础 ----笛卡尔空间轨迹规划插值代码

0.前言

我今早陷入了沉思，我想不起自己为啥要写一个逆运算包括今天这个笛卡尔空间位置和姿态插值的代码了，我在VS2019里进行仿真也不现实，我想用matlab仿真那为啥不用
matlab语言写，更何况我的毕设是在ros平台下仿真的！
但是我后来顿悟了，我是为了了解笛卡尔空间轨迹规划过程中的插值原理，尤其是四元数用于姿态的插值！我最终探讨的问题是：
如何实验笛卡尔空间下直线和圆弧的轨迹规划
并且在关节空间保证速度、加速度、加加速度的光滑！
PS：如果你不在乎原理，建议直接打开ROS 的 catkin_UR功能包进行使用！肯定比我写的好~

1.摘要

本片文章主要内容是书写笛卡尔空间的轨迹规划（PTP），插值部分的代码，输入为Ta，Tb，输出为T1，T2 、、、T100，中间的插值矩阵，实现直线的插值。

2.数学基础

2.1旋转矩阵和四元数之间的换算
公式截图来自博客https://blog.csdn.net/M_try/article/details/82900500
（这是一篇旋转变换表示换算很完整的博客）

若已知旋转矩阵R，求四元数[q0 q1 q2 q2]

则对应的四元数为：

这个来自我自己博客嘻嘻

**

2.2四元数线性插值

**
线性插值基本原理： quat_temp = quat1 + s*(quat2 - quat1)
推荐教材https://www.qiujiawei.com/understanding-quaternions/
或者其实你不看教材，也不影响这篇文章的阅读，就是高中复数的推广
我看四元数的插值分为直线，slerp等等，在我本专栏的第二篇文章中有写四元数各种插值的理论

https://blog.csdn.net/weixin_44168457/article/details/112710515

但是我这篇文章写的是PTP（点到点），所以我就简单用了线性插值，包括px，py，pz，我也没想明白可以用三次多项式或者三次样条之类，我看matlab用的是三次多项式，估计是增加了二次约束条件（边界速度约束），这个我后边文章应该会写到。

3代码

3.1第一部分是不加插值，只进行旋转矩阵的四元数换算

//笛卡尔空间PTP轨迹规划的位置和姿态插值代码编写
#include
#include"math.h"
using namespace  std;
const double d1 = 0.1273;
const double a2 = 0.612;
const double a3 = 0.5723;
const double d4 = 0.163941;
const double d5 = 0.1157;
const double d6 = 0.0922;
const double ZERO_THRESH = 0.00000001;
const double PI = 3.1415926;
void forward(const double* q, double* T) {
     
    double s1 = sin(*q), c1 = cos(*q); q++;
    double q23 = *q, q234 = *q, s2 = sin(*q), c2 = cos(*q); q++;
    double s3 = sin(*q), c3 = cos(*q); q23 += *q; q234 += *q; q++;
    double s4 = sin(*q), c4 = cos(*q); q234 += *q; q++;
    double s5 = sin(*q), c5 = cos(*q); q++;
    double s6 = sin(*q), c6 = cos(*q);
    double s23 = sin(q23), c23 = cos(q23);
    double s234 = sin(q234), c234 = cos(q234);

    *T = c6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * s6; T++;  //nx
    *T = -s6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * c6; T++;  //Ox
    *T = -(c234 * c1 * s5 - c5 * s1); T++;//ax
    *T = -(d6 * c234 * c1 * s5 - a3 * c23 * c1 - a2 * c1 * c2 - d6 * c5 * s1 - d5 * s234 * c1 - d4 * s1); T++;//Px

    *T = -c6 * (c1 * s5 - c234 * c5 * s1) - s234 * s1 * s6; T++;//ny
    *T = s6 * (c1 * s5 - c234 * c5 * s1) - s234 * c6 * s1; T++;//Oy
    *T = -(c1 * c5 + c234 * s1 * s5); T++;//ay
    *T = -(d6 * (c1 * c5 + c234 * s1 * s5) + d4 * c1 - a3 * c23 * s1 - a2 * c2 * s1 - d5 * s234 * s1); T++;//py


    *T = -(-c234 * s6 - s234 * c5 * c6); T++;//nz
    *T = -(s234 * c5 * s6 - c234 * c6); T++;//oz
    *T = -s234 * s5; T++;//az
    *T = d1 + a3 * s23 + a2 * s2 - d5 * (c23 * c4 - s23 * s4) - d6 * s5 * (c23 * s4 + s23 * c4); T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}
void OuputT(double t[4][4])

{
     
    
    
    cout << "输出矩阵T:   " << endl;
    for (int i = 0; i < 4; i++)
    {
     
        for (int j = 0; j < 4; j++)
        {
     
            cout << t[i][j] << "      ";
        }
        cout << endl;
    }
}
void OuputQuat(double quat[4])

{
     
    cout << "四元数quat：" << " [  " << quat[0] << "   " << quat[1] << "   " << quat[2] << "   " << quat[3] << "  ] " << endl;

   
}
void Quat_to_Dcm(double quat[4], double* T)
{
     
    double q0 = quat[0], q1 = quat[1],q2 = quat[2] ,q3 = quat[3];
    *T = q0*q0+q1*q1-q2*q2-q3*q3; T++;  //T00
    *T = 2*(q1*q2 - q0*q3); T++;  //T01
    *T = 2 * (q1 * q3 + q0 * q2); T++;//T02
    *T = 0; T++;//Px

    *T = 2 * (q1 * q2 +q0 * q3); T++;//ny  T10
    *T = q0 * q0 +-q1 * q1 + q2 * q2 - q3 * q3; T++;//Oy   T11
    *T = 2 * (q2 * q3 - q0 * q1); T++;//ay   T12
    *T = 0; T++;//py


    *T = 2 * (q1 * q3 - q0 * q2); T++;//nz  T20
    *T = 2 * (q3 * q2 + q0 * q1); T++;//oz   T21
    *T = q0 * q0 + -q1 * q1 - q2 * q2 +q3 * q3; T++;//az  T22
    *T = 0; T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}
void Dcm_to_Quat(double T[4][4],double * Quat)
{
     
    double q0, q1, q2, q3;
    q0 = 0.5 * sqrt(1 + T[0][0] + T[1][1] + T[2][2]);
    q1 = (T[2][1] - T[1][2]) / (4 * q0);
    q2 = (T[0][2] - T[2][0]) / (4 * q0);
    q3 = (T[1][0] - T[0][1]) / (4 * q0);
    *Quat = q0; Quat++;  *Quat = q1; Quat++;  *Quat=q2; Quat++; *Quat = q3;


}
void Ctraj(double T1, double T2, int t)
{
     
    cout << endl;
}
int main()

{
     
    double quat[4];//quat为四元数
	double q[6] = {
      0.1 ,0.2,0.3,0.4,0.5,0.6 };//q为关节角度
    double t[4][4];
    double* T, * Q,* Quat;
    T = &t[0][0];
    Q = &q[0];
    Quat = &quat[0];
    forward(Q, T);//手打矩阵T过于麻烦，所以我还是用正运动学根据q算出来的
    OuputT(t);//相对于上一篇博客，这里我把矩阵和数组的打印都封装为函数了
    Dcm_to_Quat(t, Quat);
    OuputQuat(quat);
    Quat_to_Dcm(quat,T);
    OuputT(t);
}

运行结果

输出由q 进行正运动学结果T:
0.0473957      -0.976785      -0.208915      1.18382
-0.392918      0.174058      -0.90295      -0.127305
0.918351      0.124882      -0.375547      0.416715
0      0      0      1
四元数quat： [  0.459866   0.558768   -0.612823   0.317411  ]
输出四元数计算得到的旋转矩阵T:
0.0473957      -0.976785      -0.208915      0
-0.392918      0.174058      -0.90295        0
0.918351      0.124882      -0.375547        0
0      0      0      1

可以看出来位置矩阵我还没加上 Px，Py，Pz位置是0，下边插值算法中会加上的哈~
3.2完整版插值代码

//笛卡尔空间PTP轨迹规划的位置和姿态插值代码编写
#include
#include"math.h"
using namespace  std;
const double d1 = 0.1273;
const double a2 = 0.612;
const double a3 = 0.5723;
const double d4 = 0.163941;
const double d5 = 0.1157;
const double d6 = 0.0922;
const double ZERO_THRESH = 0.00000001;
const double PI = 3.1415926;
int SIGN(double x)
{
     
    return (x > 0) - (x < 0);
}
void forward(const double* q, double* T) {
     
    double s1 = sin(*q), c1 = cos(*q); q++;
    double q23 = *q, q234 = *q, s2 = sin(*q), c2 = cos(*q); q++;
    double s3 = sin(*q), c3 = cos(*q); q23 += *q; q234 += *q; q++;
    double s4 = sin(*q), c4 = cos(*q); q234 += *q; q++;
    double s5 = sin(*q), c5 = cos(*q); q++;
    double s6 = sin(*q), c6 = cos(*q);
    double s23 = sin(q23), c23 = cos(q23);
    double s234 = sin(q234), c234 = cos(q234);

    *T = c6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * s6; T++;  //nx
    *T = -s6 * (s1 * s5 + c234 * c1 * c5) - s234 * c1 * c6; T++;  //Ox
    *T = -(c234 * c1 * s5 - c5 * s1); T++;//ax
    *T = -(d6 * c234 * c1 * s5 - a3 * c23 * c1 - a2 * c1 * c2 - d6 * c5 * s1 - d5 * s234 * c1 - d4 * s1); T++;//Px

    *T = -c6 * (c1 * s5 - c234 * c5 * s1) - s234 * s1 * s6; T++;//ny
    *T = s6 * (c1 * s5 - c234 * c5 * s1) - s234 * c6 * s1; T++;//Oy
    *T = -(c1 * c5 + c234 * s1 * s5); T++;//ay
    *T = -(d6 * (c1 * c5 + c234 * s1 * s5) + d4 * c1 - a3 * c23 * s1 - a2 * c2 * s1 - d5 * s234 * s1); T++;//py


    *T = -(-c234 * s6 - s234 * c5 * c6); T++;//nz
    *T = -(s234 * c5 * s6 - c234 * c6); T++;//oz
    *T = -s234 * s5; T++;//az
    *T = d1 + a3 * s23 + a2 * s2 - d5 * (c23 * c4 - s23 * s4) - d6 * s5 * (c23 * s4 + s23 * c4); T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}
int inverse(const double* T, double* q_sols, double* q) {
     
    int num_sols = 0;
    double T00 = *T; T++; double T01 = *T; T++; double T02 = *T; T++; double T03 = *T; T++;
    double T10 = *T; T++; double T11 = *T; T++; double T12 = *T; T++; double T13 = *T; T++;
    double T20 = *T; T++; double T21 = *T; T++; double T22 = *T; T++; double T23 = *T;
    double qq1, qq2, qq3, qq4, qq5, qq6;

    // shoulder rotate joint (q1) //
    double q1[2];
    {
     
        double A = d6 * T12 - T13;
        double B = d6 * T02 - T03;
        double R = A * A + B * B;
        if (fabs(A) < ZERO_THRESH) {
     
            double div;
            if (fabs(fabs(d4) - fabs(B)) < ZERO_THRESH)
                div = -SIGN(d4) * SIGN(B);
            else
                div = -d4 / B;
            double arcsin = asin(div);
            if (fabs(arcsin) < ZERO_THRESH)
                arcsin = 0.0;
            if (arcsin < 0.0)
                q1[0] = arcsin + 2.0 * PI;
            else
                q1[0] = arcsin;
            q1[1] = PI - arcsin;
        }
        else if (fabs(B) < ZERO_THRESH) {
     
            double div;
            if (fabs(fabs(d4) - fabs(A)) < ZERO_THRESH)
                div = SIGN(d4) * SIGN(A);
            else
                div = d4 / A;
            double arccos = acos(div);
            q1[0] = arccos;
            q1[1] = 2.0 * PI - arccos;
        }
        else if (d4 * d4 > R) {
     
            return num_sols;
        }
        else {
     
            double arccos = acos(d4 / sqrt(R));
            double arctan = atan2(-B, A);
            double pos = arccos + arctan;
            double neg = -arccos + arctan;
            if (fabs(pos) < ZERO_THRESH)
                pos = 0.0;
            if (fabs(neg) < ZERO_THRESH)
                neg = 0.0;
            if (pos >= 0.0)
                q1[0] = pos;
            else
                q1[0] = 2.0 * PI + pos;
            if (neg >= 0.0)
                q1[1] = neg;
            else
                q1[1] = 2.0 * PI + neg;
        }

        qq1 = q1[1];
    }
    

    // wrist 2 joint (q5) //
    double q5[2][2];
    {
     
        for (int i = 0; i < 2; i++) {
     
            double numer = (T03 * sin(q1[i]) - T13 * cos(q1[i]) - d4);
            double div;
            if (fabs(fabs(numer) - fabs(d6)) < ZERO_THRESH)
                div = SIGN(numer) * SIGN(d6);
            else
                div = numer / d6;
            double arccos = acos(div);
            q5[i][0] = arccos;
            q5[i][1] = 2.0 * PI - arccos;
        }

        qq5 = q5[1][0];
    }
    

    {
     
        for (int i = 0; i < 2; i++) {
     
            for (int j = 0; j < 2; j++) {
     
                double c1 = cos(q1[i]), s1 = sin(q1[i]);
                double c5 = cos(q5[i][j]), s5 = sin(q5[i][j]);
                double q6;
                // wrist 3 joint (q6) //
                if (fabs(s5) < ZERO_THRESH)
                    q6 = 0;
                else {
     
                    q6 = atan2(SIGN(s5) * -(T01 * s1 - T11 * c1),
                        SIGN(s5) * (T00 * s1 - T10 * c1));
                    if (fabs(q6) < ZERO_THRESH)
                        q6 = 0.0;
                    if (q6 < 0.0)
                        q6 += 2.0 * PI;
                }
                

                double q2[2], q3[2], q4[2];
                / RRR joints (q2,q3,q4) 
                double c6 = cos(q6), s6 = sin(q6);
                double x04x = -s5 * (T02 * c1 + T12 * s1) - c5 * (s6 * (T01 * c1 + T11 * s1) - c6 * (T00 * c1 + T10 * s1));
                double x04y = c5 * (T20 * c6 - T21 * s6) - T22 * s5;
                double p13x = d5 * (s6 * (T00 * c1 + T10 * s1) + c6 * (T01 * c1 + T11 * s1)) - d6 * (T02 * c1 + T12 * s1) +
                    T03 * c1 + T13 * s1;
                double p13y = T23 - d1 - d6 * T22 + d5 * (T21 * c6 + T20 * s6);

                double c3 = (p13x * p13x + p13y * p13y - a2 * a2 - a3 * a3) / (2.0 * a2 * a3);
                if (fabs(fabs(c3) - 1.0) < ZERO_THRESH)
                    c3 = SIGN(c3);
                else if (fabs(c3) > 1.0) {
     
                    // TODO NO SOLUTION
                    continue;
                }
                double arccos = acos(c3);
                q3[0] = arccos;
                q3[1] = 2.0 * PI - arccos;
                double denom = a2 * a2 + a3 * a3 + 2 * a2 * a3 * c3;
                double s3 = sin(arccos);
                double A = (a2 + a3 * c3), B = a3 * s3;
                q2[0] = atan2((A * p13y - B * p13x) / denom, (A * p13x + B * p13y) / denom);
                q2[1] = atan2((A * p13y + B * p13x) / denom, (A * p13x - B * p13y) / denom);
                double c23_0 = cos(q2[0] + q3[0]);
                double s23_0 = sin(q2[0] + q3[0]);
                double c23_1 = cos(q2[1] + q3[1]);
                double s23_1 = sin(q2[1] + q3[1]);
                q4[0] = atan2(c23_0 * x04y - s23_0 * x04x, x04x * c23_0 + x04y * s23_0);
                q4[1] = atan2(c23_1 * x04y - s23_1 * x04x, x04x * c23_1 + x04y * s23_1);
                qq6 = q6;
                qq2 = q2[0];
                qq3 = q3[0];
                qq4 = q4[0];


                
                for (int k = 0; k < 2; k++) {
     
                    if (fabs(q2[k]) < ZERO_THRESH)
                        q2[k] = 0.0;
                    else if (q2[k] < 0.0) q2[k] += 2.0 * PI;
                    if (fabs(q4[k]) < ZERO_THRESH)
                        q4[k] = 0.0;
                    else if (q4[k] < 0.0) q4[k] += 2.0 * PI;
                    q_sols[num_sols * 6 + 0] = q1[i];    q_sols[num_sols * 6 + 1] = q2[k];
                    q_sols[num_sols * 6 + 2] = q3[k];    q_sols[num_sols * 6 + 3] = q4[k];
                    q_sols[num_sols * 6 + 4] = q5[i][j]; q_sols[num_sols * 6 + 5] = q6;



                    num_sols++;
                }

            }
        }
    }
    *q = qq1; q++; *q = qq2; q++; *q = qq3; q++; *q = qq4; q++; *q = qq5; q++; *q = qq6;

    return num_sols;
}
void OutputT(double t[4][4])

{
     
    
    
    cout << "输出由q 进行正运动学结果T:   " << endl;
    for (int i = 0; i < 4; i++)
    {
     
        for (int j = 0; j < 4; j++)
        {
     
            cout << t[i][j] << "      ";
        }
        cout << endl;
    }
}
void OuputQuat(double quat[4])

{
     
    cout << "四元数quat：" << " [  " << quat[0] << "   " << quat[1] << "   " << quat[2] << "   " << quat[3] << "  ] " << endl;

   
}
void OutputQ(double q[6])

{
     
    cout << "关节角度q：" << " [  " << q[0] << "   " << q[1] << "   " << q[2] << "   " << q[3] <<  "   " << q[4] <<"   " << q[5] <<"  ] " << endl;


}
void Quat_to_Dcm(double quat[4], double* T)
{
     
    double q0 = quat[0], q1 = quat[1],q2 = quat[2] ,q3 = quat[3];
    *T = q0*q0+q1*q1-q2*q2-q3*q3; T++;  //T00
    *T = 2*(q1*q2 - q0*q3); T++;  //T01
    *T = 2 * (q1 * q3 + q0 * q2); T++;//T02
    *T = 0; T++;//Px

    *T = 2 * (q1 * q2 +q0 * q3); T++;//ny  T10
    *T = q0 * q0 +-q1 * q1 + q2 * q2 - q3 * q3; T++;//Oy   T11
    *T = 2 * (q2 * q3 - q0 * q1); T++;//ay   T12
    *T = 0; T++;//py


    *T = 2 * (q1 * q3 - q0 * q2); T++;//nz  T20
    *T = 2 * (q3 * q2 + q0 * q1); T++;//oz   T21
    *T = q0 * q0 + -q1 * q1 - q2 * q2 +q3 * q3; T++;//az  T22
    *T = 0; T++;//Pz
    *T = 0.0; T++; *T = 0.0; T++; *T = 0.0; T++; *T = 1.0;//姿态
}
void Dcm_to_Quat(double T[4][4],double * Quat)
{
     
    double q0, q1, q2, q3;
    q0 = 0.5 * sqrt(1 + T[0][0] + T[1][1] + T[2][2]);
    q1 = (T[2][1] - T[1][2]) / (4 * q0);
    q2 = (T[0][2] - T[2][0]) / (4 * q0);
    q3 = (T[1][0] - T[0][1]) / (4 * q0);
    *Quat = q0; Quat++;  *Quat = q1; Quat++;  *Quat=q2; Quat++; *Quat = q3;


}
void Ctraj(double T1[4][4], double T2[4][4], int t)
{
     
    for (double i = 0; i <= t;i++)
    {
     
        double T_temp[4][4]; double* T_Temp = &T_temp[0][0];
        double q[6];// double* Q = &q[0];
        double s = i / t;
        
        //姿态部分
        double quat1[4], quat2[4], quat_temp[4];
        double* Quat1 = &quat1[0], * Quat2 = &quat2[0], * Quat_temp = &quat_temp[0];
        Dcm_to_Quat(T1, Quat1); Dcm_to_Quat(T2, Quat2);
        //quat   quat_temp = quat1 + s(quat2 - quat1)
        quat_temp[0] = quat1[0] + s * (quat2[0] - quat1[0]);
        quat_temp[1] = quat1[1] + s * (quat2[1] - quat1[1]);
        quat_temp[2] = quat1[2] + s * (quat2[2] - quat1[2]);
        quat_temp[3] = quat1[3] + s * (quat2[3] - quat1[3]);
        Quat_to_Dcm(quat_temp, T_Temp);
        
        //位置部分
        
        double p1[3], p2[3], p_temp[3];
        p1[0] = T1[0][3]; p1[1] = T1[1][3]; p1[2] = T1[2][3];
        p2[0] = T2[0][3]; p2[1] = T2[1][3]; p2[2] = T2[2][3];
        //p_temp = p1 + s(p2-p1)   s(0→1）(p1→p2)
        p_temp[0] = p1[0] + s * (p2[0] - p1[0]); p_temp[1] = p1[1] + s * (p2[1] - p1[1]); p_temp[2] = p1[2] + s * (p2[2] - p1[2]); 
        T_temp[0][3] = p_temp[0]; T_temp[1][3] = p_temp[1]; T_temp[2][3] = p_temp[2];
        double q_sols[48]; int num_sols;
        num_sols = inverse(T_Temp, q_sols, q);
        cout <<endl<<"i = "<< i << endl ;
        OutputT(T_temp); OutputQ(q);
    }
}
int main()

{
     
    double qa[6] = {
      0.1 ,0.2,0.3,0.4,0.5,0.6 }, qb[6] = {
      0.7 ,0.8,0.9,1.0,1.1,1.2 };//q为关节角度
    double ta[4][4], tb[4][4];
    double* Qa = &qa[0], * Qb = &qb[0], * Ta = &ta[0][0], * Tb = &tb[0][0];
    forward(Qa, Ta); forward(Qb, Tb);
    cout << "初始矩阵Ta： " << endl;OutputT(ta); cout << "终止矩阵Tb： " << endl; OutputT(tb);    
    int t = 10;
    Ctraj(ta, tb, t);
    

}

我每次粘贴的代码都是完整代码，包含里边需要的函数，所以不要将我不同PART的代码放在一起·运行，会出bug
运行结果

初始矩阵Ta：
输出由q 进行正运动学结果T:
0.0473957      -0.976785      -0.208915      1.18382
-0.392918      0.174058      -0.90295      -0.127305
0.918351      0.124882      -0.375547      0.416715
0      0      0      1
终止矩阵Tb：
输出由q 进行正运动学结果T:
-0.210275      -0.361227      0.90846      0.496913
-0.599338      0.781771      0.172127      0.149518
-0.772385      -0.508281      -0.380884      1.20334
0      0      0      1

i = 0
输出由q 进行正运动学结果T:
0.0473957      -0.976785      -0.208915      1.18382
-0.392918      0.174058      -0.90295      -0.127305
0.918351      0.124882      -0.375547      0.416715
0      0      0      1
关节角度q： [  0.1   0.2   0.3   0.4   0.5   0.6  ]

i = 1
输出由q 进行正运动学结果T:
0.141285      -0.705088      -0.18535      1.11513
-0.190259      0.146597      -0.702692      -0.0996231
0.703779      0.181178      -0.152755      0.495377
0      0      0      1
关节角度q： [  0.114481   0.25323   0.305191   -0.0345366   0.827227   0.834109  ]

i = 2
输出由q 进行正运动学结果T:
0.208583      -0.480089      -0.142192      1.04644
-0.0372217      0.138742      -0.523045      -0.0719408
0.499318      0.210893      0.0204082      0.574039
0      0      0      1
关节角度q： [  0.132933   0.00588692   0.717431   2.32152   1.04768   4.40191  ]

i = 3
输出由q 进行正运动学结果T:
0.249292      -0.301788      -0.079439      0.977747
0.0661928      0.150496      -0.364009      -0.0442585
0.304967      0.214028      0.143944      0.652701
0      0      0      1
关节角度q： [  0.156335   0.0162988   0.948902   1.35948   1.21621   4.84737  ]

i = 4
输出由q 进行正运动学结果T:
0.26341      -0.170185      0.00290758      0.909056
0.119985      0.181856      -0.225584      -0.0165762
0.120728      0.190582      0.217852      0.731363
0      0      0      1
关节角度q： [  0.186033   0.102284   1.01767   0.627397   1.3467   5.0304  ]

i = 5
输出由q 进行正运动学结果T:
0.250938      -0.0852805      0.104848      0.840366
0.124154      0.232824      -0.107771      0.0111061
-0.0534012      0.140556      0.242132      0.810025
0      0      0      1
关节角度q： [  0.223918   0.212333   1.02929   0.0164071   1.44208   4.97203  ]

i = 6
输出由q 进行正运动学结果T:
0.211876      -0.0470737      0.226383      0.771675
0.0787007      0.303399      -0.0105691      0.0387884
-0.217419      0.0639497      0.216785      0.888687
0      0      0      1
关节角度q： [  0.272726   0.350961   0.984728   -0.54655   1.49958   4.77372  ]

i = 7
输出由q 进行正运动学结果T:
0.146223      -0.0555649      0.367511      0.702984
-0.0163752      0.393581      0.0660218      0.0664707
-0.371327      -0.0392372      0.141809      0.967349
0      0      0      1
关节角度q： [  0.336517   0.526787   0.857911   -1.01752   1.51173   4.55033  ]

i = 8
输出由q 进行正运动学结果T:
0.0539806      -0.110754      0.528233      0.634294
-0.161074      0.50337      0.122001      0.094153
-0.515124      -0.169005      0.0172059      1.04601
0      0      0      1
关节角度q： [  0.421512   0.757787   0.598733   -1.32418   1.4658   4.38912  ]

i = 9
输出由q 进行正运动学结果T:
-0.0648523      -0.212641      0.70855      0.565603
-0.355395      0.632767      0.15737      0.121835
-0.648809      -0.325352      -0.157025      1.12467
0      0      0      1
关节角度q： [  0.537494   0.62214   1.00414   1.29131   1.3412   1.17569  ]

i = 10
输出由q 进行正运动学结果T:
-0.210275      -0.361227      0.90846      0.496913
-0.599338      0.781771      0.172127      0.149518
-0.772385      -0.508281      -0.380884      1.20334
0      0      0      1
关节角度q： [  0.7   0.8   0.9   1   1.1   1.2  ]

3.3matlab的仿真结果验证
代码

%%
%标准DH参数表
%通用格式L = Link（[alpha A seita D seigema],CONVENTION）
clc
L1 = Link([0 0.1273 0 pi/2 0],'standard');
L2 = Link([0 0 0.612 0 0],'standard');
L3 = Link([0 0 0.5723 0 0],'standard');
L4 = Link([0 0.163941 0 pi/2 0],'standard');
L5 = Link([0 0.1157 0 -pi/2 0],'standard');
L6 = Link([0 0.0922 0 0 0],'standard');
ur10 = SerialLink([L1 L2 L3 L4 L5 L6]);
qa = [0.1,0.2,0.3,0.4,0.5,0.6];
qb = [0.7,0.8,0.9,1.0,1.1,1.2];
Ta = ur10.fkine(qa);
Tb = ur10.fkine(qb);
t = 0:0.1:1;
Ts = ctraj(Ta,Tb,length(t));
for i = 1:11
    
     Ts(i)
     %q = ur10.ikine(Ts(i))
end

运行结果

ans = 
    0.0474   -0.9768   -0.2089     1.184
   -0.3929    0.1741   -0.9030   -0.1273
    0.9184    0.1249   -0.3755    0.4167
         0         0         0         1
 

ans = 
    0.1086   -0.9672   -0.2297     1.168
   -0.3345    0.1820   -0.9247   -0.1211
    0.9361    0.1772   -0.3037    0.4344
         0         0         0         1
 

ans = 
    0.2951   -0.9187   -0.2626     1.122
   -0.1552    0.2251   -0.9619   -0.1024
    0.9428    0.3246   -0.0762    0.4875
         0         0         0         1
 

ans = 
    0.5850   -0.7815   -0.2167     1.045
    0.1272    0.3524   -0.9272  -0.07125
    0.8010    0.5149    0.3056     0.576
         0         0         0         1
 

ans = 
    0.8423   -0.5388    0.0139    0.9434
    0.3851    0.5836   -0.7150  -0.03042
    0.3771    0.6076    0.6990     0.692
         0         0         0         1
 

ans = 
    0.8804   -0.2992    0.3679    0.8404
    0.4356    0.8169   -0.3781   0.01111
   -0.1874    0.4931    0.8495      0.81
         0         0         0         1
 

ans = 
    0.6801   -0.1513    0.7174    0.7373
    0.2551    0.9662   -0.0381   0.05263
   -0.6873    0.2089    0.6957     0.928
         0         0         0         1
 

ans = 
    0.3191   -0.1463    0.9364     0.636
   -0.0858    0.9795    0.1823   0.09346
   -0.9438   -0.1385    0.3000     1.044
         0         0         0         1
 

ans = 
    0.0107   -0.2392    0.9709    0.5587
   -0.3831    0.8959    0.2249    0.1246
   -0.9237   -0.3743   -0.0821     1.133
         0         0         0         1
 

ans = 
   -0.1591   -0.3276    0.9313    0.5124
   -0.5489    0.8134    0.1924    0.1433
   -0.8206   -0.4806   -0.3093     1.186
         0         0         0         1
 

ans = 
   -0.2103   -0.3612    0.9085    0.4969
   -0.5993    0.7818    0.1721    0.1495
   -0.7724   -0.5083   -0.3809     1.203
         0         0         0         1

matlab关于机器人的功能包可以看我资源分享有一个PPT，写的很是完整，来自学校老师的课程。

matlab代码中有一行注释，就是我尝试算出q（i）然后打印，像我C++语言实现的一样，但是matlab自带的逆运动学求解代码不咋地，有的算不出来。

4.总结

本文实现了UR10机器人在笛卡尔空间下轨迹规划的C++代码编写，实现了线性插值，其中旋转矩阵插值使用四元数插值。
该文章存在两个待解决的问题
一个是我编写的笛卡尔轨迹规划代码输出是直接在函数出输出到srceen上，但是这样是不对的，应该用指针返回，对我有点难嘻嘻嘻~我明天会改！
第二个是可以看出我输出的插值矩阵，和matlab输出的不一样，可能的原因我在上文提到过，是因为matlab用的应该不是线性插值，所以没办法确认旋转矩阵的四元数插值是百分百正正确，我尝试逆运动学输出去，看起来没有问题。我在下文会进行旋转矩阵的图形显示，来确保一下！