ICCV2019《Recursive Cascaded Networks for Unsupervised Medical Image Registration》代码学习

ICCV2019《Recursive Cascaded Networks for Unsupervised Medical Image Registration》代码学习

该论文代码为tensorflow，本学习过程最终目的是将该tensorflow代码改写为pytorch
Github代码链接：Recursive Cascaded Networks for Unsupervised Medical Image Registration

eval.py 跑通

1、按照要求将所需val datasets以及pretrain的model下载到指定文件夹。
2、ModuleNotFoundError: No module named 'tensorflow.compat’问题解决参考 No module named ‘tensorflow.compat’
3、tensorflow1.4.0对应keras版本为2.0.8
4、注意tensorflow1.4.0需要安装cuda8.0以及cuDNN6.0，参考 CUDA 8.0 + cuDNN v6.0安装 (Linux).
5、tensorflow.python.framework.errors_impl.InternalError: Dst tensor is not initialized 一般是GPU内存耗尽，如果没有多余GPU资源，可以将batchsize改小。注意GPU要能均分batchsize，所以GPU数要小于等于batchsize!!!
6、最终可实现Github中的描述，结果以txt存下来并与论文一致(pre-trained的model肯定一样)，如下图：
brain-val：LPBA

liver-val：SLIVER

liver-val：LiTS

liver-val：LSPIG

train.py 跑通

GPU资源不够，VTN-10目前跑不起来，如下图：

改为尝试 VTN-1，batchsize = 2, liver case, 其它参数默认，训练及测试结果如下图：

由于训练100000 steps耗时过长 (~50h， 1 card of 12 GB NVIDIA TITAN V), 训练了约30000 steps停了下来：

在各liver-val测试结果：
SLIVER：文章 Dice = 0.914, Lm.Dist. = 13.0

LiTS：文章 Dice = 0.870

LSPIG：文章 Dice = 0.833

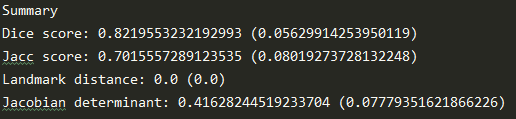
performance不如文章原因，可能是训练的steps不足，没有最终收敛到一个更优的解。

demo.py 跑通

由于没有符合要求的input image，故没有尝试运行。不过为了查看real_flow， wraped_moving，image_fixed等可视化结果，参考Recursive Cascaded Networks for Unsupervised Medical Image Registration issue#14修改。
a sample from SLIVER
自己train的model可视化：VTN-1 steps ~30000
fixed image：

moving image:

wraped_moving:

pre-train model可视化：VTN-10
wraped_moving:

flow: z=64
VTN-10 pre-train model

VTN-1 my preliminarily train model

PS：也可以提取中间层该层的flow field，agg_flow(累计到某层为止的flow field)，warped_image等具体见代码recursive_cascaded_networks.py line 179。

fast_reconstruction在Ubuntu下不可用

代码初步理解

由于笔者是深度学习小白，对tensorflow以及python高级用法都不熟悉，所以采取了在debug模式下一行一行查函数，一行一行理解的笨办法。
在理解代码之前，复习或新学习了一些常用的python语法 Python学习。
代码结构：
train.py:
1、主要包括用Linux运行时，命令行要输入参数的设置。
2、tensorflow graph的建立(损失函数，网络结构)。
3、循环设置，log保存，model保存。
Dataset:
预处理数据 - > generator供train调取。
network:
1、base_network:VoxelMorph、VTN第一层仿射层，VTN后边级联的可变形层网络结构。
2、recursive cascaded_network:级联控制，每一层loss的计算，权重参数等。
3、framework：整体框架。
4、spatial_transformer: 根据学习到的flow做图像矫正。
5、utils: Network父类，被base_network中的类继承，等
6、trilinear_sampler,transform:一些“零散”子函数，还未仔细看。

数据集

该工作所用数据集包括公开和非公开的数据集：
Liver
1、MSD challenge :包括10个task，这篇文章选了3个与liver相关的 (Task03，07，08)。数据集具体情况参见 arXiv Link
Task03: liver and tumors，contrast-enhanced CT 多中心，label为专家标注的分割annotations。
Task07:胰腺，因为靠肝脏近，所以也用了进来。
Task10: 肝脏肿瘤，肝脏血管。
2、BFH (北京友谊医院): 非公开的数据集，也用于了他们之前的工作 VTN，未知label有无及类型。
3、SLIVER: 公开数据集，label为分割annotations以及landmark。SLIVER 07: train 20 test 10，但是该文章只用了train的20，因为test的10没有label，没法评估。SLIVER 这个数据集也是 VTN中MICCAI 07
4、LiTS: 公开数据集，label为分割annotations(结果也有landmark dist的评估，所有应该也有(landmark label)。LiTS
5、LSPIG：非公开数据集，猪的肝数据，label为分割annotations。
Brain
1、ADNI: 阿尔兹海默症的公开脑部数据集，需要注册申请使用，可能一些百度云也有，ADNI。
2、ABIDE: 自闭症脑部公开数据集，ABIDE
3、ADHD: 注意缺陷综合症公开数据集，需要注册，ADHD
4、LPBA: 公开数据集 LPBA

数据预处理

文章说的比较模糊：大概就是降采到128*128*128，然后crop（liver数据集中一个简单阈值来找liver大致位置然后crop，后面也手动筛掉了一些crop不好的），直方图均衡（辐射剂量不同）。

评估指标

Dice：[0, 1]，分割区域完全不对齐和完全对齐：文章公式分子应该为交
$2\ast |seg1\cap seg2|/(|seg1|+|seg2|)$
landmark dist：对应key point的距离
LiTS结果也有landmark dist，但是文章没给出。
代码也给出了Jacc score和雅可比行列式的结果，但是文章没给出。
Jacc score:
$|seg1\cap seg2|/(|seg1\cup seg2|)$
雅可比行列式:
初步了解，参考 雅可比行列式与形变场评价

代码深度理解

读取数据集

作者把数据集预处理为HDF5格式。HDF5格式的数据，笔者完全不了解，这里做一个简单学习 HDF5。

Spatial Transformer

在代码的spatial transformer.py中有Dense3DSpatialTransformer这个类，这个类继承了keras的Layer类之后，能够完成根据给定的flow field给出moving image的warped image的功能。其中build, call, compute_output_shape三个方法是和Layer有交互，最终call方法是这个类的实例调用的方法(类似于直接定义类的__call__方法)。其中最为关键的一步是怎么插值出warped image不在grid点上的像素值。代码中提到了Dense3DSpatialTransformer这个类的实现参考了VoxelMorph中的实现，VoxelMorph中的实现如下图所描述，论文链接VoxelMorph：

其思想为，当moving image的grid加上flow field之后，很可能因为flow field对应的位移值不是整数像素，从而使得位移后对应的点不在moving image的grid上，如上图所示，这时候就可以根据周围8领域进行一个插值，插出该点的像素值，每个邻域的权重如VoxelMorph文章中所述，是每个维度距离的乘积。

数据增强

在代码framework.py中定义了网络的框架，其中有数据增强的部分，具体为代码中关于sample_power，free_form_fields以及warp_points等函数被使用的地方。

sample_power

这个函数笔者的理解是，随机产生控制点的位移，从而为后面free_form_fields根据产生的控制点的位移产生数据增强的flow field，再使用spatial transformer.py中的Dense3DSpatialTransformer这个类产生增强后的image，因为控制点的位移是在某个范围内随机的，所以这样可以极大提高数据的多样性，在github的issue中有人提到，可以直接使用这几个函数，对fixed image和moving image都做数据增强，在原代码中，作者只对moving image做了数据增强。根据代码，每一个体数据被resize为128x128x128，代码中的control field grid也就是控制点的grid是均匀分布的5x5x5，因为是三维数据每个点都有3个方向的位移，所以是5x5x5x3的size的control field。代码中给的上下限分别为0.4，-0.4，笔者的理解是，因为control field grid是均匀分布的，间隔为128/(5 - 1) = 32，这里的上下限0.4代码随机的位移最大为0.4x32个像素(可能是和数据集有关，代码作者可能看了自己的数据集，觉得位移量大概最大为32*0.4)。

free_form_fields

这个函数是基于产生的control fields。用三次B样条插值，插出完整的要增强的flow field,size为128x128x128与原体数据大小一致。笔者查询了一些论文，发现大多数论文包括较早的一些，例如 Deformable Medical Image Registration: A Survey 等提到关于基于B样条函数的Free Form Deformations(FFD)都是直接用了B样条基函数。

笔者找了很多文献，多是直接写出来，如下图：

PS：注意上两图中的nx或者Nx应该是错误的，对应位置应该是均匀控制点的间距。
在找了一些资料后，在《Computer Graphics with OpenGL》第三版这本书中，找到了关于B样条基函数的解释。
样条曲线的概念是：数学上多使用分段三次多项式函数来描述这种曲线，其中各曲线段的连接处有连续的一次和二次导数。在计算机图像学中，样条曲线指由多项式曲线段连接而成的曲线，在每段的边界处满足特定的连续性条件，例如，0阶、1阶、2阶边界条件等。
给定一组点(控制点)，根据这组点插值和逼近的概念是不同的，插值要求选取的每段多项式曲线要经过控制点，而逼近则不需要满足该条件，即某些控制点或者全部控制点可以不在生成的样条曲线上，如下图所示：

一般对于三次样条描述，我们习惯用待定系数法，例如一些博客中提到的：三次样条插值，通过增加边界条件，从而可以得到与待定系数个数相同的方程组，进而求出三次样条插值函数。但这只是样条描述的一种方法，其实给定多项式的阶数以及控制点位置(坐标以及值)后，我们可以有三个等价的方法来描述样条函数：(1)列出一组加在样条上的边界条件(就是上述待定系数的方法)。(2)列出描述样条特征的行列式。(3)列出一组混合函数或者基函数，确定如何组合指定的曲线几何约束(这里的几何约束可以理解为该控制点的位移值或者叫做位置，或者是该控制点处的斜率，这个根据所用样条不同而不同，即上述关于FFD的文章中所说的d或者$\varphi$)，来计算曲线路径上的位置或者叫做位移值。

假设沿着样条路径有某一段，我们用三次多项式表示为：
$x(u)=a_x{u}^3+b_x{u}^2+c_{x}u+d_x,0\le u\le 1(1)$
这里为什么要求 $0\le u\le 1$,是因为如果样条路径的某一段范围是[a,b]，你可以做一个线性变换归一化到[0,1],所以这里不失一般性，我们这里就用了[0,1]范围(这里的理解稍不确定)。该曲线的边界条件可以设为端点坐标$x(0),x(1)$以及端点处的一次导数$x^{\prime }(0)$和$x^{\prime }(1)$。这四个边界条件是确定系数$a_x,b_x,c_x,d_x$的充分条件，为什么说是充分条件，目前笔者的理解是，样条路径通常会包括好几个控制点，每两个控制点间都要确定一个样条多项式表示，综合起来看这几段样条多项式，在中间控制点有固有的等式条件三次样条插值，也就是说，不需要每段样条多项式都给出四个边界条件，只需要在最两端的控制点给出2个边界条件(1阶或者2阶或者周期边界条件)就可以得到4n个方程(n为样条曲线的分段数，控制点个数为n+1)，所以这里一段样条多项式就给出了边界条件，是充分不必要条件。

我们可以将$(1)$式写成向量相乘的形式：
$x(u)=\left[\begin{array}{cccc}{u}^3& u^2& u& 1\end{array}\right]\left[\begin{array}{c}{a}_x\\ b_x\\ c_x\\ d_x\end{array}\right]=UC(2)$
U称为参数u的幂次行矩阵，C是系数列矩阵。
其中我们可以令$C=M_{spline}{M}_{geom}$，M_{geom}是包含样条上的几何约束值(边界条件)的四元素列矩阵，M_{spline}是4x4矩阵，将几何约束值转化成多项式系数.
本例中，$M_{spline}=\left[\begin{array}{cccc}2& -2& 1& 1\\ -3& 3& -2& -1\\ 0& 0& 1& 0\\ 1& 0& 0& 0\end{array}\right]$, $M_{geom}=\left[\begin{array}{c}x(0)\\ x(1)\\ x^{\prime }(0)\\ x^{\prime }(1)\end{array}\right]$
上式也被称为Hermite插值，此时的$M_{spline}$也记为$M_H$
将U和$M_{spline}$相乘就可以得到混合函数(基函数)。

除了Hermite插值，还有cardinal样条插值，Kochanek-Bartels样条插值，Bezier样条插值以及B-spline样条插值。B-spline插值就是free_form_fields函数中所用的插值方法，关于其他插值，这里不再赘述，详情可看《Computer Graphics with OpenGL》第三版这本书中8.9 三次样条插值方法内容，这里给出一个资源链接 计算机图形学第三版
cardinal样条插值与Hermite插值不同的是，它不需要给出端点的切线值，即Hermite插值中的$x^{\prime }(0),x^{\prime }(1)$，cardinal样条中一个控制点的斜率值可以通过相邻控制点算出，Kochanek-Bartels样条插值式cardinal样条的变种，通过引入两个参数可以提供更为灵活的三次多项式表示。Bezier样条插值多数情况下是一个阶数比控制点少1的多项式，而B样条多项式次数可以独立于控制点数目，但一般也是选择比控制点数少1。

根据笔者对代码以及B样条的理解，代码中用的是三次周期性B样条曲线，如下图所示：

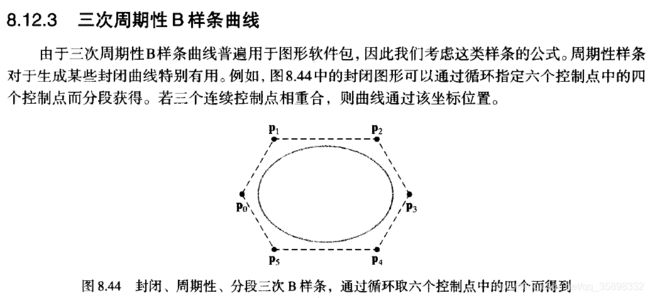
从边界条件角度推导三次周期性B样条曲线的基函数：
仍旧是考虑 $0\le u\le 1$，因为三次B样条需要一般需要四个控制点，所以如果我们要插值某一段样条路径，我们还需要该路径端点两侧相邻的各一个端点，如果我们是第一段或者最后一段路径，那么我们就需要类似padding去补齐前一个或者后一个已经超出节点范围的“隐式”节点，这样才能做插值，free_form_fields程序中是将5x5x5的control field的grid padding为7x7x7，值为0，即“隐式”节点的位移为0。B样条的边界条件如下：记四个控制点为$p_{-1},p_0,p_1,p_2$(我们要插值的样条路径段为节点$p_0,p_1$之间的那段)
$P(0)=\frac{1}{6}(p_{-1}+4p_0+p_2)$
$P(1)=\frac{1}{6}(p_0+4p_1+p_2)$
$P^{\prime }(0)=\frac{1}{2}(p_1-p_{-1})$
$P^{\prime }(1)=\frac{1}{2}(p_2-p_0)$
其中$p_{-1},p_0,p_1,p_2$就代表控制点的位移值。所以三次周期B样条的边界条件也不需要切线值。
再根据前面$M_{spline}$的计算方法，我们也可以计算出三次周期B样条的边界条件的$M_{spline}$，记为$M_B$：
$M_B=\frac{1}{6}\left[\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 3& 0\\ -3& 0& 3& 0\\ 1& 4& 1& 0\end{array}\right]$
将$U=\left[\begin{array}{cccc}{u}^3& u^2& u& 1\end{array}\right]$与$M_B$相乘，就可以得到三次周期B样条的基函数。即一直不理解的：

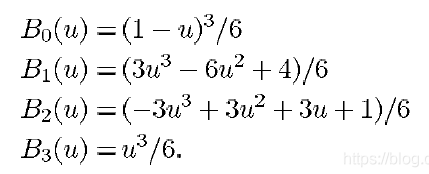
warp_points

因为数据增强除了要对image进行增强外，moving image的landmark也要根据前面产生的flow field进行变换。从要配准的图像对角度，flow field是从fixed image到moving image的flow field。而在这个数据增强的过程中，这里所说的fixed image其实是指的要配准图像对中的moving image增强后的image, 而moving image仍是要配准图像对中的moving image。如下图所示：

我们对image进行增强的时候，是将fixed image的grid加上registraion flow然后生成的坐标位置，用前面提到的spatial transformer去插值出该坐标在moving image中的值，然后放入对应的fixed image的grid的位置。而将landmark变换的时候其实这个过程是相反的，即不是从moving image插值放入fixed image的grid，而是直接对fixed landmark加上fixed landmark位置的registration flow，这个坐标就是根据配准结果得到moving landmark的坐标(注意这里的坐标不是ground truth的moving landmark)。由于landmark通常是小数，也就是我们需要根据registration flow来插值出landmark位置处的flow,这个过程仍旧是与Spatial Transformer中的相同，是一个三次线性的过程。但是在数据增强的过程中，我们的fixed landmark其实是augmented landmark，是我们想要根据augmented flow得到的，所以我们只能根据moving landmark和augented flow来反推这个过程的fixed landmark，也就是augmented landmark，如下图所示：

这个反推的过程，就不能像“正”方向那样直接三次线性插值，插出fixed landmark所在位置的registration flow，进而可以“精确”得到moving landmark的坐标。而是先用Augmented image(数据增强过程的fixed image)的grid + Augmented flow得到moving grid，然后找moving landmark最近邻的moving grid点，当作moving landmark的近似，然后对应回Augmented image的grid点，这个grid点的坐标就“近似”为Augmented landmark的坐标。
这样虽然可以实现对landmark的增强，但是其实严格来说是“不准确”的。

recursive_cascaded_network

这里定义了递归级联网络的结构，VTNAffineStem是VTN网络的第一层仿射层，VTN是后面级联的deformable层。raw_weight是similarity的权重，在之前他们VTN的工作中第一层仿射层也使用了similarity的权重，但是在递归级联网络中，只有最后一层deformable层有similarity权重。第一层的仿射层只用了orthogonality loss和determinant loss,中间的deformable层(除去最后一层)只使用了regularization loss(smooth term)，最后一层deformable层使用了regularization loss和similarity loss。
每个loss term的权重是orthogonality loss的权重是0.1, determinant loss权重是0.1， regularization loss和similarity loss的权重都是1。网络中每一层的子网络还有一个自己的权重，这里的仿射层和每一层deformable的权重都是1。
base_networks中定义了仿射层，可变性层，以及VoxelMorph。

VTNAffineStem定义了仿射层

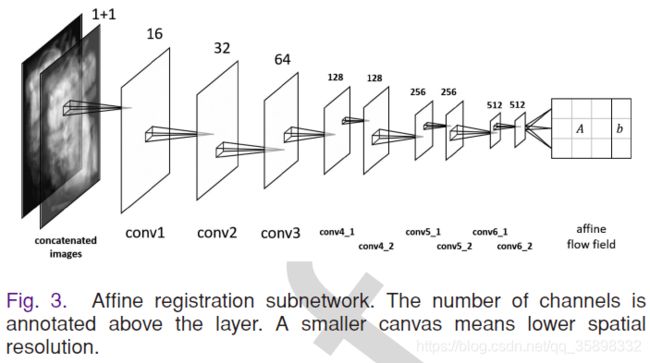
仿射层的结构如上图所示(代码中实现，多一个stride为1的64conv)，最后生成了仿射矩阵A以及平移向量b。特别注意：文章提到的f(x)=Ax+b是flow field或者叫displacement field，不是通常仿射变换得到的place position，这里主要的区别是相差了一个单位矩阵I，即A + I是我们通常理解的仿射矩阵。
关于仿射层的loss有两个特殊的正则化term，一个是determinant loss，一个是orthogonality loss：
1、orthogonality loss: 正交loss，这个loss的理解如文章描述

结合代码的实现，这个loss的逻辑，笔者的理解是：首先基于代码作者关于数据集的先验知识，即医学图像配准中，每对图像的初步仿射配准是一个刚性配准，即只包含(平移，反射，旋转)，上面文章提到small scaling，近似认为没有scaling(loss设置以及代码实现也反映了这一点)。刚性配准的变换矩阵是一个正交矩阵，下图给出了一个二维的例子，可以结合旋转变换矩阵自行验证：

即这里的A + I最终的优化结果是一个正交矩阵。从loss function角度出发，orthogonality loss是想让$(I+A{)}^T(I+A)$的三个特征值都close to 1，结合$(I+A{)}^T(I+A)$矩阵是一个实对称矩阵，所以我们可以推出，$(I+A{)}^T(I+A)$的优化结果是一个单位矩阵(特征值都为1的实对称矩阵是单位矩阵)，而根据正交矩阵的定义，$(I+A{)}^T(I+A)$是单位矩阵，那(I + A)就是正交矩阵，所以优化结果的变换矩阵是刚性变换，符合一开始的先验知识。
2、determinant loss：行列式loss，这个loss的设置主要是为了避免刚性变换中的反射操作。
如orthogonality loss所述，刚性变换包括反射，平移，旋转，而平移是我们这里的表示形式下是被平移向量控制，不包含在变换矩阵中，所以现在通过orthogonality loss约束了变换矩阵是正交矩阵，也就约束了刚性变换——旋转或者反射。但是如文章中所述，医学图像默认手性相同：

即我们要避免变换矩阵有反射操作。其实反射操作可以理解是scaling系数为-1的scaling操作。为什么Ldet可以避免反射操作呢？其实笔者的理解是Ldet避免了不同维度奇数次反射操作，因为不同维度的偶数次反射操作会把手性再变回来，如下图所示(二维例子)：

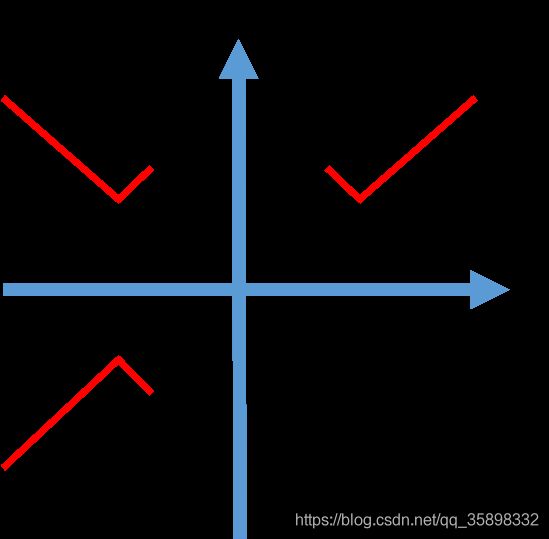
第一象限的对号图案，如果只关于y轴反射一次，手性就改变了，如果想要通过后续的deformable层配准起来，就需要有folding，但后续的deformable层都有smooth term，避免出现这种情况。而进行两次反射，即变到第三象限，就可以通过一个简单的旋转配准起来，即没有手性的改变。所以我们要避免的是奇数次反射操作。因为我们的变换矩阵已经因为orthogonality loss的约束是一个正交阵，但是正交阵的行列式取值可以是+1或者-1,经过偶数次反射变换结合旋转变换，行列式的值仍是+1，经过奇数次的行列式的值是-1，当det(A + I)是1是，Ldet=0，当是-1是，Ldet=4，仍较大，所以Ldet避免了奇数次反射变化，也就是避免了手性的改变。
疑问: 关于仿射层，笔者还有两个地方没有理解：
1、affine_flow函数，根据仿射层卷积后生成的W和b来计算仿射层的flow field，其默认原点位置为三维数据的中心，但是笔者没有找到充分理由来解释为什么。不过可以肯定的是，原点位置的不同只会影响b，不会影响W。
2、elem_sym_polys_of_eigen_values函数：如VTN文章中关于orthogonality loss的描述，代码作者使用了韦达定理来计算orthogonality loss，代码中的实现将orthogonality loss做了一个变形：
$L_{ortho}=-6+{\sum }_{i=1}^3({\lambda }_i^2+{\lambda }_i^{-2})=-6(1+eps)+{\sum }_{i=1}^3{\lambda }_i^2+(1+eps{)}^2\frac{{\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_1^2{\lambda }_3^2}{{\prod }_{i=1}^3{\lambda }_i^2}$
其中${\lambda }_i^2$是矩阵$(I+A{)}^T(I+A)$的特征值，上述${\sum }_{i=1}^3{\lambda }_i^2$等于矩阵的迹，${\prod }_{i=1}^3{\lambda }_i^2$等于矩阵的行列式的值。但代码中关于${\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_1^2{\lambda }_3^2$的实现，是将矩阵$(I+A{)}^T(I+A)$看成是对角矩阵然后使用对角分块矩阵的结论进行计算，虽然最终的优化目标是把$(I+A{)}^T(I+A)$优化成单位矩阵，但是笔者的理解是，中间过程的$(I+A{)}^T(I+A)$可能不是一个对角矩阵，代码中${\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_1^2{\lambda }_3^2$实现可能不正确，这一点仍需确认。
回答：
1、这里默认fixed image的原点在中心，b根据网络学习，所以最后flow field产生的时候，是以fixe image的grid产生，所以要按照中心在原点去定义像素点的位置。

VTN定义了可变形层

VTN的结构借鉴了U-net结构，代码实现与上图有轻微出入，64的conv有两层，第二层stride=1，不改变feature大小;且在两个512conv后加了一个conv生成这个尺度下的flow prediction，后面会把同一尺度的deconv和conv以及flow prediction去concatenated起来去生成尺寸上大一尺度的flow prediction以及deconv。
疑问：
1、在deconv的过程中，代码中都是用的kernal size=4, 这不太符合与conv对称的直觉，笔者目前还未理解。
2、最后输出的flow field代码中*20，笔者也未理解原因。

agg_flow的计算

笔者看到级联结果中关于agg_flow也就是“累积”flow的计算的时候，不太理解，结合VTN的文章最终理解，VTN中关于这部分的内容如下图：

stem_result['agg_flow'] = self.reconstruction(
	[stem_results[-1]['agg_flow'], stem_result['flow']]) + stem_result['flow'] 

上面代码对应的就是VTN的公式(3)
在代码的实现中，代码作者把第一个deformable层和非第一个deformable层分开计算agg_flow，笔者的理解是都可以按照上述代码来计算，但是由于第一个deformable层是级联在仿射层后面的，算是一种特殊情况，可以利用这个先验知识来简化运算，毕竟直接用self.reconstruction(也就是Dense3DSpatialTransformer)做插值，运算可能还是比较大的。
对于第一个deformable层这个特殊情况，只需要把VTN文章中(2)式相应的$g_1$变为仿射变换的方程就可以了，推导过程如下：
$warp(warp(I,g_1),g_2)(x)=warp(warp(I,aff),def)(x)=I(x+def(x)+aff(x+def(x)))=I(x+def(x)+A(x+def(x))+b)=I((I+A)x+(I+A)def(x)+b)=warp(I,f)$
其中$f(x)=(I+A)def(x)+Ax+b$，即agg_flow，与代码中的实现一致，代码的实现如下：代码中的W对应文章中的A，stem_results[-1][‘flow’]就是$Wx+b$对应这里的$Ax+b$。

stem_result['agg_flow'] = tf.einsum('bij,bxyzj->bxyzi', 
	stem_results[-1]['W'] + I, stem_result['flow']) + stem_results[-1]['flow']

loss的计算

相似度loss和正则化loss代码实现与VTN文章完全一致。
雅可比矩阵的实现与VoxelMorph以及雅可比行列式与形变场评价一致，代码中多加了一个单位矩阵，是因为flow field是displacement不是position。
每一层的总loss还要乘以一个层的权重，这个权重在代码中都设置为1了，即每个层“同样重要”。但是deformable层的flow field乘了一个权重，权重为(1/deformable层的总层数)。

train & eval

RenderFlow in eval

疑问：
笔者目前只大概理解这个函数是对z=64的flow field slice做可视化，但是还不明白这个函数一些具体参数的选择以及代码对应操作的实际意义。

tensorflow & pytorch学习

train.py以及eval.py的大部分内容与tensorflow框架有关，笔者对tensorflow还不太熟悉，另外笔者要把代码改成pytorch，故首先选择熟悉tensorflow tensorflow学习 以及pytorch pytorch学习 框架。

Pytorch复现

长时间未更新，因为在用pytorch复现的时候出现了很多问题，目前可以达到差不多的效果，但是还是有一些问题，在此做一个记录，等结果完全一样再release代码。

目前存在的问题

1、Pytorch版本目前不知道为何，占用内存很大，一块卡只能级联3层，Tensorflow version测试的时候可以级联到7层（但是理论上应该可以到10层，可能原因是没有用Fast3DTransformer或者当时服务器其他人的程序占用CPU资源较多，但是Fast3DTransformer没有Linux版本，这个没法改变），故下面很多目前的结果都先针对仿射+级联一层deformable做测试，等结果一样再回头解决这个问题。
2、Pytorch版本用多卡进行测试的时候，det_jaccabian metric会随机出现极少量nan，目前还未解决，先都在1块卡测试，等程序结果差不多再回过头解决这个问题。
2、Landmark效果上还是与Tensorflow version存在一定差距，直觉感觉是因为训练出来的Jacobian det的值与Tensorflow版本有一定差距，i.e.Pytorch训练出来的flow不够平滑，直觉感觉陷入了一个不够好的局部最优。

目前达到的效果

如果没有特殊说明，batch=1，train in one card, evaluation in one card，Tensorflow version和Pytorch version程序所有参数设置（学习率，优化器，训练steps，loss weight，初始化方式）都是一样的。所有结果都是liver case。

初始化

Pytorch和Tensorflow的默认初始化是不一样的，对于卷积权重的初始化Pytorch是kaiming_uniform，而Tensorflow是uniform_scaling；对于bias的初始化，Pytorch是一个上下界与kernel_size，ouput_channels, input_channels有关的均匀分布，而Tensorflow是全0初始化。
以三维为例，具体的公式为：
设三维卷积的权重W.shape=[kernelsize, kernelsize,kernelsize, inputchannels, ouputchannels]
kaiming_uniform：
W均匀分布上下界：
$bound=\frac{\sqrt{3}\times gain}{\sqrt{kernelsiz{e}^3\times inputchannels}}$
$gain=\frac{1}{\sqrt{3}}$
bias均匀分布上下界同上
uniform_scaling：
W均匀分布上下界：
$bound=\frac{\sqrt{3}}{\sqrt{kernelsiz{e}^3\times inputchannels}}$
代码如下：

# Custom initialization corresponding to Tensorflow version in Github
# https://github.com/microsoft/Recursive-Cascaded-Networks
def weight_init(m):
    if isinstance(m, nn.Conv3d):
        input_size = 1
        for dim in list(m.weight.shape[1:]):
            input_size *= float(dim)
        init.uniform_(m.weight.data, a=-math.sqrt(3 / input_size), b=math.sqrt(3 / input_size))
        if m.bias is not None:
            init.constant_(m.bias.data, 0)
    if isinstance(m, nn.ConvTranspose3d):
        input_size = 1
        for dim in list(m.weight.shape[1:]):
            input_size *= float(dim)
        init.uniform_(m.weight.data, a=-math.sqrt(3 / input_size), b=math.sqrt(3 / input_size))
        if m.bias is not None:
            init.constant_(m.bias.data, 0)

Affine Only

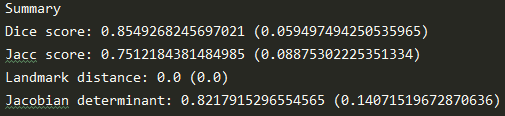
目前在只用仿射层时候的结果，Pytorch和Tensorflow的结果还是一致的。

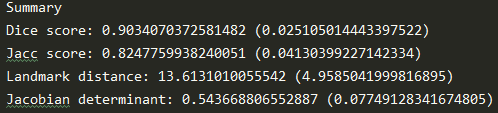
Affine + 1层deformable

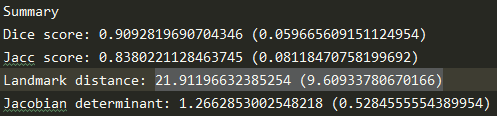
Landmark distance有比较大的差异，Jacobian det反应flow粗糙程度。
训练出来的总的flow场如下，Pytorch的要更粗糙：
Tensorflow version z=64

Pytorch version z=64

级联初步结果

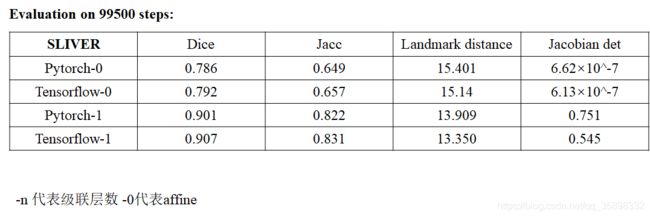
Pytorch version初始化以及网络结构(原来代码encoder kernel size=4)没改过来情况下，级联到3层的结果：梯度还是在的，但就是达不到Tensorflow的performance，-n代码deformable级联层数。





##########################2021/02/12更新##############################
Tensorflow version和Pytorch version的padding方式不同，反卷积的padding方式目前相同（笔者目前验证了二维的情况，当Tensorflow以及Pytorch反卷积函数设置如下时，出来的结果是一样的）：
Tensorflow version:

// Tensorflow version
import tensorflow as tf

test1 = tf.constant(1.0, shape=[1,4,4,1])

w = tf.constant(1.0, shape=[4,4,1,1])
result = tf.nn.conv2d_transpose(test1, w, output_shape=[1,8,8,1], strides=[1,2,2,1],padding="SAME")

with tf.Session() as sess:
    print(sess.run(result))

Pytorch version:

// Pytorch version
import torch.nn as nn
import torch

test1 = torch.ones([1,1,4,4])

upconv = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=4, stride=2, padding=1, bias=False)
upconv.weight = nn.Parameter(torch.ones(upconv.weight.shape))

result = upconv(test1)
print(result)

但是卷积的padding方式Pytorch和Tensorflow不太一样：
当Pytorch卷积函数，指定好padding数以及kernel size后，卷积最终结果是遵循Tensorflow中‘valid’的padding方式的，优先舍弃右下，而Tensorflow的‘same’的padding方式，当对称（左上，右下都补0）padding后不足够满足卷积的需求时，优先保留右下的padding。笔者通过Pytorch代码中设置不padding，在每个卷积层之前手动设置padding(图像指定位置补0)以保持与Tensorflow一致，结果如下，区别仍旧不大：