CHAPTER 12 Statistical Parsing
CHAPTER 12 Statistical Parsing
Speech and Language Processing ed3 读书笔记
It is possible to build probabilistic models of syntactic knowledge and use some of this probabilistic knowledge to
build efficient probabilistic parsers.
One crucial use of probabilistic parsing is to solve the problem of disambiguation. The most commonly used probabilistic grammar formalism is the probabilistic context-free grammar (PCFG), a probabilistic augmentation of context-free grammars in which each rule is associated with a probability.
12.1 Probabilistic Context-Free Grammars
A probabilistic context-free grammar (PCFG) is also defined by four parameters, with a slight augmentation to each of the rules in R R R:
N N N: a set of non-terminal symbols (or variables)
Σ \Sigma Σ: a set of terminal symbols (disjoint from N N N)
R R R: a set of rules or productions, each of the form A → β [ p ] A\to \beta\ [p] A→β [p] , where A A A is a non-terminal, β \beta β is a string of symbols from the infinite set of strings ( Σ ∪ N ) ∗ (\Sigma \cup N)^∗ (Σ∪N)∗ , and p p p is a number between 0 and 1 expressing P ( β ∣ A ) P(\beta|A) P(β∣A)
S S S: a designated start symbol and a member of N N N
A PCFG differs from a standard CFG by augmenting each rule in R R R with a conditional probability:
A → β [ p ] A \to \beta\ [p] A→β [p]
Here p p p expresses the probability that the given non-terminal A A A will be expanded to the sequence β \beta β. That is, p p p is the conditional probability of a given expansion β \beta β given the left-hand-side (LHS) non-terminal A A A. We can represent this probability as
P ( A → β ) P(A \to \beta) P(A→β)
or as
P ( A → β ∣ A ) P(A \to \beta|A) P(A→β∣A)
or as
P ( R H S ∣ L H S ) P(RHS|LHS) P(RHS∣LHS)
Thus, if we consider all the possible expansions of a non-terminal, the sum of their probabilities must be 1:
∑ β P ( A → β ) = 1 \sum_\beta P(A \to \beta) = 1 β∑P(A→β)=1
Figure 12.1 shows a PCFG: a probabilistic augmentation of the L 1 \mathscr{L}_1 L1 miniature English CFG grammar and lexicon.
A PCFG is said to be consistent if the sum of the probabilities of all sentences in the language equals 1.
12.1.1 PCFGs for Disambiguation
A PCFG assigns a probability to each parse tree T T T (i.e., each derivation) of a sentence S S S. This attribute is useful in disambiguation.
The probability of a particular parse T T T is defined as the product of the probabilities of all the n n n rules used to expand each of the n n n non-terminal nodes in the parse tree T T T, where each rule i i i can be expressed as L H S i → R H S i LHS_i \to RHS_i LHSi→RHSi:
P ( T , S ) = ∏ i = 1 n P ( R H S i ∣ L H S i ) P(T,S) = \prod_{i=1}^n P(RHS_i|LHS_i) P(T,S)=i=1∏nP(RHSi∣LHSi)
The resulting probability P ( T , S ) P(T,S) P(T,S) is both the joint probability of the parse and the sentence and also the probability of the parse P ( T ) P(T) P(T). Given a parse tree, the sentence is determined, i.e., P ( S ∣ T ) P(S|T) P(S∣T) is 1.
P ( T , S ) = P ( T ) P ( S ∣ T ) = P ( T ) P(T,S) = P(T)P(S|T)=P(T) P(T,S)=P(T)P(S∣T)=P(T)
Consider all the possible parse trees for a given sentence S S S. The string of words S S S is called the yield of any parse tree over S S S. Thus, out of all parse trees with a yield of S, the disambiguation algorithm picks the parse tree that is most probable given S:
T ^ ( S ) = arg max T s . t . S = yield ( T ) P ( T ∣ S ) \hat T(S) = \mathop{\arg\max}_{T\ s.t.\ S=\textrm{yield}(T)} P(T|S) T^(S)=argmaxT s.t. S=yield(T)P(T∣S)
By definition, the probability P ( T ∣ S ) P(T|S) P(T∣S) can be rewritten as P ( T , S ) / P ( S ) P(T,S)/P(S) P(T,S)/P(S), thus leading to
T ^ ( S ) = arg max T s . t . S = yield ( T ) P ( T , S ) P ( S ) \hat T(S) = \mathop{\arg\max}_{T\ s.t.\ S=\textrm{yield}(T)}\frac{P(T,S)}{P(S)} T^(S)=argmaxT s.t. S=yield(T)P(S)P(T,S)
Since we are maximizing over all parse trees for the same sentence, P(S) will be a constant for each tree, so we can eliminate it:
T ^ ( S ) = arg max T s . t . S = yield ( T ) P ( T , S ) \hat T(S) = \mathop{\arg\max}_{T\ s.t.\ S=\textrm{yield}(T)} P(T,S) T^(S)=argmaxT s.t. S=yield(T)P(T,S)
Furthermore, since we showed above that P ( T , S ) = P ( T ) P(T,S) = P(T) P(T,S)=P(T), the final equation for choosing the most likely parse neatly simplifies to choosing the parse with the highest probability:
T ^ ( S ) = arg max T s . t . S = yield ( T ) P ( T ) \hat T(S) = \mathop{\arg\max}_{T\ s.t.\ S=\textrm{yield}(T)} P(T) T^(S)=argmaxT s.t. S=yield(T)P(T)
12.1.2 PCFGs for Language Modeling
A second attribute of a PCFG is that it assigns a probability to the string of words constituting a sentence. This is important in language modeling, whether for use in speech recognition, machine translation, spelling correction, augmentative communication, or other applications. The probability of an unambiguous sentence is P ( T , S ) = P ( T ) P(T,S) = P(T) P(T,S)=P(T) or just the probability of the single parse tree for that sentence. The probability of an ambiguous sentence is the sum of the probabilities of all the parse trees for the sentence:
P ( S ) = ∑ T s . t . S = yield ( T ) P ( T , S ) = ∑ T s . t . S = yield ( T ) P ( T ) P(S) =\sum_{T\ s.t.\ S=\textrm{yield}(T)} P(T,S)\\ =\sum_{T\ s.t.\ S=\textrm{yield}(T)} P(T) P(S)=T s.t. S=yield(T)∑P(T,S)=T s.t. S=yield(T)∑P(T)
PCFG is useful for language modeling.
P ( w i ∣ w 1 , w 2 , … , w i − 1 ) = P ( w 1 , w 2 , … , w i − 1 , w i ) P ( w 1 , w 2 , … , w i − 1 ) P(w_i|w_1,w_2,\ldots,w_{i-1}) = \frac{P(w_1,w_2,\ldots,w_{i-1},w_i)}{P(w_1,w_2,\ldots,w_{i-1})} P(wi∣w1,w2,…,wi−1)=P(w1,w2,…,wi−1)P(w1,w2,…,wi−1,wi)
12.2 Probabilistic CKY Parsing of PCFGs
def find_in_set(set_find,element):
for e in set_find:
if element.lower()==e.lower():
return True
return False
build_tree(back,table):
vocs=['incluses','the','a','meal','flight'] #terminals
non_terms=['S','NP', 'VP','Det','N','V'] #non-terminals
n=len(words)
table =[[{
nt:0. for nt in non_terms} for i in range(n+1)] for i in range(n+1)]
back=[[{
nt:[] for nt in non_terms} for i in range(n+1)] for i in range(n+1)]
def probability_CKY(words,grammars):
for j in range(1,n+1):
for grammar,prob in grammars.items():
ind=grammar.find(':-')
if(grammar[ind+2:].lower().find(words[j-1].lower())!=-1):
table[j-1][j][grammar[:ind].strip()]=prob
for i in range(j-2,-1,-1):
for k in range(i+1,j):
for grammar,prob in grammars.items():
ind=grammar.find(':-')
BC=grammar[ind+2:].split()
if len(BC)==2 and table[i][k][BC[0]]>0 and table[k][j][BC[1]]>0:
if table[i][j][grammar[:ind].strip()]<prob*table[i][k][BC[0]]*table[k][j][BC[1]]:
table[i][j][grammar[:ind].strip()]=prob*table[i][k][BC[0]]*table[k][j][BC[1]]
back[i][j][grammar[:ind].strip()]=[k,BC[0],BC[1]]
return build_tree(back[1,n,S],table[1,n,S])
12.3 Ways to Learn PCFG Rule Probabilities
There are two ways to learn probabilities for the rules of a grammar. The simplest way is to use a treebank, a corpus of already parsed sentences. Given a treebank, we can compute the probability of each expansion of a non-terminal by counting the number of times that expansion occurs and then normalizing.
P ( α → β ∣ α ) = Count ( α → β ) ∑ γ Count ( α → γ ) = Count ( α → β ) Count ( α ) P(\alpha \to \beta |\alpha)=\frac{\textrm{Count}(\alpha \to \beta)}{\sum_\gamma \textrm{Count}(\alpha \to \gamma)}=\frac{\textrm{Count}(\alpha \to \beta)}{ \textrm{Count}(\alpha)} P(α→β∣α)=∑γCount(α→γ)Count(α→β)=Count(α)Count(α→β)
If we don’t have a treebank but we do have a (non-probabilistic) parser, we can generate the counts we need for computing PCFG rule probabilities by first parsing a corpus of sentences with the parser. If sentences were unambiguous, it would be as simple as this: parse the corpus, increment a counter for every rule in the parse, and then normalize to get probabilities.
But wait! Since most sentences are ambiguous, that is, have multiple parses, we don’t know which parse to count the rules in. Instead, we need to keep a separate count for each parse of a sentence and weight each of these partial counts by the probability of the parse it appears in (i.e., count each parse by the probability, not by 1 as in unambiguous case). But to get these parse probabilities to weight the rules, we need to already have a probabilistic parser.
The intuition for solving this chicken-and-egg problem is to incrementally improve our estimates by beginning with a parser with equal rule probabilities, then parse the sentence, compute a probability for each parse, use these probabilities to weight the counts, re-estimate the rule probabilities, and so on, until our probabilities converge. The standard algorithm for computing this solution is called the inside-outside algorithm; it was proposed by Baker (1979) as a generalization of the forward-backward algorithm for HMMs. Like forward-backward, inside-outside is a special case of the Expectation Maximization (EM) algorithm, and hence has two steps: the expectation step, and the maximization step. See Lari and Young (1990) or Manning and Sch u ¨ \ddot u u¨tze (1999) for a complete description of the algorithm.
This use of the inside-outside algorithm to estimate the rule probabilities for a grammar is actually a kind of limited use of inside-outside. The inside-outside algorithm can actually be used not only to set the rule probabilities but even to induce the grammar rules themselves. It turns out, however, that grammar induction is so difficult that inside-outside by itself is not a very successful grammar inducer; see the Historical Notes at the end of the chapter for pointers to other grammar induction algorithms.
12.4 Problems with PCFGs
While probabilistic context-free grammars are a natural extension to context-free grammars, they have two main problems as probability estimators:
Poor independence assumptions: CFG rules impose an independence assumption on probabilities, resulting in poor modeling of structural dependencies across the parse tree.
Lack of lexical conditioning: CFG rules don’t model syntactic facts about specific words, leading to problems with subcategorization ambiguities, preposition attachment, and coordinate structure ambiguities.
12.4.1 Independence Assumptions Miss Structural Dependencies Between Rules
The CFG independence assumption results in poor probability estimates. This is because in English the choice of how a node expands can after all depend on the location of the node in the parse tree. There is no way to capture the fact that in subject position, the probability for N P → P R P NP \to PRP NP→PRP should go from .28 up to .91, while in object position, the probability for N P → D T N N NP \to DT\ NN NP→DT NN should go from .25 up to .66.
These dependencies could be captured if the probability of expanding an NP as a pronoun (e.g., N P → P R P NP\to PRP NP→PRP) versus a lexical NP (e.g., N P → D T N N NP \to DT\ NN NP→DT NN) were conditioned on whether the NP was a subject or an object. Section 12.5 introduces the technique of parent annotation for adding this kind of conditioning.
12.4.2 Lack of Sensitivity to Lexical Dependencies
A second class of problems with PCFGs is their lack of sensitivity to the words in the parse tree. Words do play a role in PCFGs since the parse probability includes the probability of a word given a part-of-speech (i.e., from rules like V → s l e e p V \to sleep V→sleep, N N → b o o k NN \to book NN→book, etc.).
But it turns out that lexical information is useful in other places in the grammar, such as in resolving prepositional phrase (PP) attachment ambiguities. Since prepositional phrases in English can modify a noun phrase or a verb phrase, when a parser finds a prepositional phrase, it must decide where to attach it into the tree.
Thus, to get the correct parse, we need a model that somehow augments the PCFG probabilities to deal with lexical dependency statistics for different verbs and prepositions.
Coordination ambiguities are another case in which lexical dependencies are the key to choosing the proper parse.
In summary, we have shown in this section and the previous one that probabilistic context-free grammars are incapable of modeling important structural and lexical dependencies.
12.5 Improving PCFGs by Splitting Non-Terminals
One idea would be to split the NP non-terminal into two versions: one for subjects, one for objects. Having two nodes (e.g., N P s u b j e c t NP_{subject} NPsubject and N P o b j e c t NP_{object} NPobject) would allow us to correctly model their different distributional properties, since we would have different probabilities for the rule N P s u b j e c t → P R P NP_{subject} \to PRP NPsubject→PRP and the rule N P o b j e c t → P R P NP_{object} \to PRP NPobject→PRP.
One way to implement this intuition of splits is to do parent annotation (Johnson, 1998), in which we annotate each node with its parent in the parse tree. Thus, an NP node that is the subject of the sentence and hence has parent S S S would be annotated N P ^ S NP\hat{}S NP^S, while a direct object NP whose parent is VP would be annotated N P ^ V P NP\hat{}VP NP^VP.
In addition to splitting these phrasal nodes, we can also improve a PCFG by splitting the pre-terminal part-of-speech nodes (Klein and Manning, 2003b).
To deal with cases in which parent annotation is insufficient, we can also handwrite rules that specify a particular node split based on other features of the tree. For example, to distinguish between complementizer IN and subordinating conjunction IN, both of which can have the same parent, we could write rules conditioned on other aspects of the tree such as the lexical identity (the lexeme that is likely to be a complementizer, as a subordinating conjunction).
Node-splitting is not without problems; it increases the size of the grammar and hence reduces the amount of training data available for each grammar rule, leading to overfitting. Thus, it is important to split to just the correct level of granularity for a particular training set. While early models employed hand-written rules to try to find an optimal number of non-terminals (Klein and Manning, 2003b), modern models automatically search for the optimal splits. The split and merge algorithm of Petrov et al. (2006), for example, starts with a simple X-bar grammar, alternately splits the non-terminals, and merges non-terminals, finding the set of annotated nodes that maximizes the likelihood of the training set treebank. As of the time of this writing, the performance of the Petrov et al. (2006) algorithm was the best of any known parsing algorithm on the Penn Treebank.
12.6 Probabilistic Lexicalized CFGs
In this section, we discuss an alternative family of models in which instead of modifying the grammar rules, we modify the probabilistic model of the parser to allow for lexicalized rules. The resulting family of lexicalized parsers includes the well-known Collins parser (Collins, 1999) and Charniak parser (Charniak, 1997), both of which are publicly available and widely used throughout natural language processing.
We saw in Section 10.4.3 that syntactic constituents could be associated with a lexicalized grammar lexical head, and we defined a lexicalized grammar in which each non-terminal in the tree is annotated with its lexical head, where a rule like V P → V B D N P P P V P \to VBD\ NP\ PP VP→VBD NP PP would be extended as
V P ( d u m p e d ) → V B D ( d u m p e d ) N P ( s a c k s ) P P ( i n t o ) VP(dumped) \to VBD(dumped)\ NP(sacks)\ PP(into) VP(dumped)→VBD(dumped) NP(sacks) PP(into)
In the standard type of lexicalized grammar, we actually make a further extension, which is to associate the head tag, the part-of-speech tags of the headwords, with the non-terminal symbols as well. Each rule is thus lexicalized by both the headword and the head tag of each constituent resulting in a format for lexicalized rules like
V P ( d u m p e d , V B D ) → V B D ( d u m p e d , V B D ) N P ( s a c k s , N N S ) P P ( i n t o , P ) VP(dumped,VBD) \to VBD(dumped,VBD)\ NP(sacks,NNS)\ PP(into,P) VP(dumped,VBD)→VBD(dumped,VBD) NP(sacks,NNS) PP(into,P)
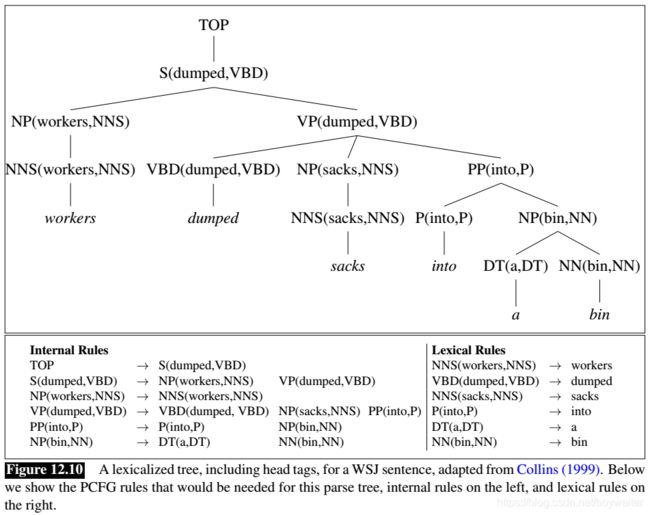
We show a lexicalized parse tree with head tags in Fig. 12.10.
To generate such a lexicalized tree, each PCFG rule must be augmented to identify one right-hand constituent to be the head daughter. The headword for a node is then set to the headword of its head daughter, and the head tag to the part-of-speech tag of the headword.
A natural way to think of a lexicalized grammar is as a parent annotation, that is, as a simple context-free grammar with many copies of each rule, one copy for each possible headword/head tag for each constituent. Thinking of a probabilistic lexicalized CFG in this way would lead to the set of simple PCFG rules shown below the tree in Fig. 12.10.
Note that Fig. 12.10 shows two kinds of rules: lexical rules, which express the expansion of a pre-terminal to a word, and internal rules, which express the other rule expansions. We need to distinguish these kinds of rules in a lexicalized grammar because they are associated with very different kinds of probabilities. The lexical rules are deterministic, that is, they have probability 1.0 since a lexicalized pre-terminal like N N ( b i n , N N ) NN(bin, NN) NN(bin,NN) can only expand to the word bin. But for the internal rules, we need to estimate probabilities.
12.6.1 The Collins Parser
The first intuition of the Collins parser is to think of the right-hand side of every (internal) CFG rule as consisting of a head non-terminal, together with the non-terminals to the left of the head and the non-terminals to the right of the head. In the abstract, we think about these rules as follows:
L H S → L m L m − 1 … L 1 H R 1 … R n − 1 R n ( 12.24 ) LHS \to L_m L_{m-1} \ldots L_1 H R_1 \ldots R_{n-1} R_n (12.24) LHS→LmLm−1…L1HR1…Rn−1Rn(12.24)
Since this is a lexicalized grammar, each of the symbols like L 1 L_1 L1 or R 3 R_3 R3 or H H H or L H S LHS LHS is actually a complex symbol representing the category and its head and head tag, like V P ( d u m p e d , V P ) VP(dumped,VP) VP(dumped,VP) or N P ( s a c k s , N N S ) NP(sacks,NNS) NP(sacks,NNS).
Now, instead of computing a single MLE probability for this rule, we are going to break down this rule via a neat generative story, a slight simplification of what is called Collins Model 1. This new generative story is that given the left-hand side, we first generate the head of the rule and then generate the dependents of the head, one by one, from the inside out. Each of these generation steps will have its own probability.
We also add a special STOP non-terminal at the left and right edges of the rule. So it’s as if we are generating a rule augmented as follows:
P ( V P ( d u m p e d , V B D ) → S T O P V B D ( d u m p e d , V B D ) N P ( s a c k s , N N S ) P P ( i n t o , P ) S T O P ) P(VP(dumped,VBD) \to STOP\ VBD(dumped, VBD)\ NP(sacks,NNS)\ PP(into,P)\ STOP) P(VP(dumped,VBD)→STOP VBD(dumped,VBD) NP(sacks,NNS) PP(into,P) STOP)

In summary, the probability of this rule
P ( V P ( d u m p e d , V B D ) → V B D ( d u m p e d , V B D ) N P ( s a c k s , N N S ) P P ( i n t o , P ) P(VP(dumped,VBD) \to VBD(dumped, VBD)\ NP(sacks,NNS)\ PP(into,P) P(VP(dumped,VBD)→VBD(dumped,VBD) NP(sacks,NNS) PP(into,P)
is estimated as
KaTeX parse error: Got function '\newline' as argument to '\begin{array}' at position 1: \̲n̲e̲w̲l̲i̲n̲e̲
Each of these probabilities can be estimated from much smaller amounts of data than the full probability. For example, the maximum likelihood estimate for the component probability P R ( N P ( s a c k s , N N S ) ∣ V P , V B D , d u m p e d ) P_R(NP(sacks,NNS)|VP, VBD, dumped) PR(NP(sacks,NNS)∣VP,VBD,dumped) is
Count ( V P ( d u m p e d , V B D ) with N N S ( s a c k s ) as a daughter somewhere on the right ) Count ( V P ( d u m p e d , V B D ) ) \frac{\textrm{Count}( VP(dumped,VBD)\ \textrm{with } NNS(sacks)\textrm{ as a daughter somewhere on the right })}{\textrm{Count}(VP(dumped,VBD) )} Count(VP(dumped,VBD))Count(VP(dumped,VBD) with NNS(sacks) as a daughter somewhere on the right )
These counts are much less subject to sparsity problems than are complex counts like those in (19).
More generally, if H H H is a head with head word h w hw hw and head tag h t , l w / l t ht, lw/lt ht,lw/lt and r w / r t rw/rt rw/rt are the word/tag on the left and right respectively, and P P P is the parent, then the probability of an entire rule can be expressed as follows:
-
Generate the head of the phrase H ( h w , h t ) H(hw, ht) H(hw,ht) with probability:
P H ( H ( h w , h t ) ∣ P , h w , h t ) P_H(H(hw, ht)|P, hw, ht) PH(H(hw,ht)∣P,hw,ht) -
Generate modifiers to the left of the head with total probability
∏ i = 1 n + 1 P L ( L i ( l w i , l t i ) ∣ P , H , h w , h t ) \prod _{i=1}^{n+1}P_L(L_i(lw_i, lt_i)|P, H, hw, ht) i=1∏n+1PL(Li(lwi,lti)∣P,H,hw,ht)
such that L n + 1 ( l w n + 1 , l t n + 1 ) = L_{n+1}(lw_{n+1}, lt_{n+1}) = Ln+1(lwn+1,ltn+1)=STOP, and we stop generating once we’ve generated a STOP token. -
Generate modifiers to the right of the head with total probability:
∏ i = 1 n + 1 P R ( R i ( r w i , r t i ) ∣ P , H , h w , h t ) \prod _{i=1}^{n+1}P_R(R_i(rw_i, rt_i)|P, H, hw, ht) i=1∏n+1PR(Ri(rwi,rti)∣P,H,hw,ht)
such that R n + 1 ( r w n + 1 , r t n + 1 ) = R_{n+1}(rw_{n+1}, rt_{n+1}) = Rn+1(rwn+1,rtn+1)= STOP, and we stop generating once we’ve generated a STOP token.
12.6.2 Advanced: Further Details of the Collins Parser
The actual Collins parser models are more complex (in a couple of ways) than the simple model presented in the previous section. Collins Model 1 conditions also on a distance feature:
P L ( L i ( l w i , l t i ) ∣ P , H , h w , h t , d i s t a n c e L ( i − 1 ) ) P_L(L_i(lw_i, lt_i)|P, H, hw, ht, distance_L(i− 1)) PL(Li(lwi,lti)∣P,H,hw,ht,distanceL(i−1))
P R ( R i ( r w i , r t i ) ∣ P , H , h w , h t , d i s t a n c e R ( i − 1 ) ) P_R(R_i(rw_i, rt_i)|P, H, hw, ht, distance_R(i− 1)) PR(Ri(rwi,rti)∣P,H,hw,ht,distanceR(i−1))
The distance measure is a function of the sequence of words below the previous modifiers (i.e., the words that are the yield of each modifier non-terminal we have already generated on the left).
The simplest version of this distance measure is just a tuple of two binary features based on the surface string below these previous dependencies: (1) Is the string of length zero? (i.e., were no previous words generated?) (2) Does the string contain a verb?
Collins Model 2 adds more sophisticated features, conditioning on subcategorization frames for each verb and distinguishing arguments from adjuncts.
Finally, smoothing is as important for statistical parsers as it was for N-gram models. This is particularly true for lexicalized parsers, since the lexicalized rules will otherwise condition on many lexical items that may never occur in training (even using the Collins or other methods of independence assumptions).
Consider the probability P R ( R i ( r w i , r t i ) ∣ P , h w , h t ) P_R(R_i(rw_i, rt_i)|P, hw, ht) PR(Ri(rwi,rti)∣P,hw,ht). What do we do if a particular right-hand constituent never occurs with this head? The Collins model addresses this problem by interpolating three backed-off models: fully lexicalized (conditioning on the headword), backing off to just the head tag, and altogether unlexicalized.
| Backoff | P R ( R i ( r w i , r t i ∣ … ) P_R(R_i(rw_i, rt_i|\ldots) PR(Ri(rwi,rti∣…) | Example |
| ------- | -------------------------------- | ---------------------------------- |
| 1 | P R ( R i ( r w i , r t i ) ∣ P , h w , h t ) P_R(R_i(rw_i, rt_i)|P, hw, ht) PR(Ri(rwi,rti)∣P,hw,ht) | P R ( N P ( s a c k s , N N S ) ∣ V P , V B D , d u m p e d PR(NP(sacks,NNS)|VP, VBD, dumped PR(NP(sacks,NNS)∣VP,VBD,dumped |
| 2 | P R ( R i ( r w i , r t i ∣ P , h t ) P_R(R_i(rw_i, rt_i|P, ht) PR(Ri(rwi,rti∣P,ht) | P R ( N P ( s a c k s , N N S ) ∣ V P , V B D ) PR(NP(sacks,NNS)|VP, VBD) PR(NP(sacks,NNS)∣VP,VBD) |
| 3 | P R ( R i ( r w i , r t i ∣ P ) P_R(R_i(rw_i, rt_i|P) PR(Ri(rwi,rti∣P) | P R ( N P ( s a c k s , N N S ) ∣ V P ) PR(NP(sacks,NNS)|VP) PR(NP(sacks,NNS)∣VP) |
Similar backoff models are built also for P L P_L PL and P H P_H PH. Although we’ve used the word “backoff”, in fact these are not backoff models but interpolated models. The three models above are linearly interpolated, where e 1 , e 2 e_1, e_2 e1,e2, and e 3 e_3 e3 are the maximum likelihood estimates of the three backoff models above:
P R ( … ) = λ 1 e 1 + ( 1 − λ 1 ) ( l 2 e 2 + ( 1 − λ 2 ) e 3 ) P_R(\ldots) = \lambda_1e_1 + (1− \lambda_1)(l_2e_2 + (1− \lambda_2)e_3) PR(…)=λ1e1+(1−λ1)(l2e2+(1−λ2)e3)
The values of λ 1 \lambda_1 λ1 and λ 2 \lambda_2 λ2 are set to implement Witten-Bell discounting (Witten and Bell, 1991) following Bikel et al. (1997).
The Collins model deals with unknown words by replacing any unknown word in the test set, and any word occurring less than six times in the training set, with a special UNKNOWN word token. Unknown words in the test set are assigned a part-of-speech tag in a preprocessing step by the Ratnaparkhi (1996) tagger, all other words are tagged as part of the parsing process.
The parsing algorithm for the Collins model is an extension of probabilistic CKY, see Collins (2003a).
12.7 Probabilistic CCG Parsing
12.7.1 Ambiguity in CCG
12.7.2 CCG Parsing Frameworks
Since the rules in combinatory grammars are either binary or unary, a bottom-up, tabular approach based on the CKY algorithm should be directly applicable to CCG parsing. Recall from Fig. 12.3 that PCKY employs a table that records the location, category and probability of all valid constituents discovered in the input. Given an appropriate probability model for CCG derivations, the same kind of approach can work for CCG parsing.
Unfortunately, the large number of lexical categories available for each word, combined with the promiscuity of CCG’s combinatoric rules, leads to an explosion in the number of (mostly useless) constituents added to the parsing table. The key to managing this explosion of zombie constituents is to accurately assess and exploit the most likely lexical categories possible for each word — a process called supertagging.
The following sections describe two approaches to CCG parsing that make use of supertags. Section 12.7.4, presents an approach that structures the parsing process as a heuristic search through the use of the A* algorithm. The following section then briefly describes a more traditional maximum entropy approach that manages the search space complexity through the use of adaptive supertagging — a process that iteratively considers more and more tags until a parse is found.
12.7.3 Supertagging
Chapter 8 introduced the task of part-of-speech tagging, the process of assigning the supertagging correct lexical category to each word in a sentence. Supertagging is the corresponding task for highly lexicalized grammar frameworks, where the assigned tags often dictate much of the derivation for a sentence.
As with traditional part-of-speech tagging, the standard approach to building a CCG supertagger is to use supervised machine learning to build a sequence classifier using labeled training data. A common approach is to use the maximum entropy Markov model (MEMM), as described in Chapter 8, to find the most likely sequence of tags given a sentence. The features in such a model consist of the current word w i w_i wi, its surrounding words within l l l words w i − l i + l w_{i -l}^{i+ l} wi−li+l, as well as the k k k previously assigned supertags t i − k i − 1 t_{i-k}^{i-1} ti−ki−1. This type of model is summarized in the following equation from Chapter 8. Training by maximizing log-likelihood of the training corpus and decoding via the Viterbi algorithm are the same as described in Chapter 8.
KaTeX parse error: Expected group after '_' at position 27: …athop{\arg\max}_̲\limits TP(T|W)…
The single best tag sequence T ^ \hat T T^ will typically contain too many incorrect tags for effective parsing to take place. To overcome this, we can instead return a probability distribution over the possible supertags for each word in the input. The following table illustrates an example distribution for a simple example sentence.
In a MEMM framework, the probability of the optimal tag sequence defined in Eq. 28 is efficiently computed with a suitably modified version of the Viterbi algorithm. However, since Viterbi only finds the single best tag sequence it doesn’t provide exactly what we need here; we need to know the probability of each possible word/tag pair. The probability of any given tag for a word is the sum of the probabilities of all the supertag sequences that contain that tag at that location. A table representing these values can be computed efficiently by using a version of the forward-backward algorithm used for HMMs.
The same result can also be achieved through the use of deep learning approaches based on recurrent neural networks (RNNs). Recent efforts have demonstrated considerable success with RNNs as alternatives to HMM-based methods. These approaches differ from traditional classifier-based methods in the following ways:
- The use of vector-based word representations (embeddings) rather than word-based feature functions.
- Input representations that span the entire sentence, as opposed to size-limited sliding windows.
- Avoiding the use of high-level features, such as part of speech tags, since errors in tag assignment can propagate to errors in supertags.
As with the forward-backward algorithm, RNN-based methods can provide a probability distribution over the lexical categories for each word in the input.
12.7.4 CCG Parsing using the A* Algorithm
The A* algorithm is a heuristic search method that employs an agenda to find an optimal solution. Search states representing partial solutions are added to an agenda based on a cost function, with the least-cost option being selected for further exploration at each iteration. When a state representing a complete solution is first selected from the agenda, it is guaranteed to be optimal and the search terminates.
The A* cost function, f ( n ) f (n) f(n), is used to efficiently guide the search to a solution. The f f f-cost has two components: g ( n ) g(n) g(n), the exact cost of the partial solution represented by the state n n n, and h ( n ) h(n) h(n) a heuristic approximation of the cost of a solution that makes use of n n n. When h ( n ) h(n) h(n) satisfies the criteria of not overestimating the actual cost, A* will find an optimal solution. Not surprisingly, the closer the heuristic can get to the actual cost, the more effective A* is at finding a solution without having to explore a significant portion of the solution space.
When applied to parsing, search states correspond to edges representing completed constituents. As with the PCKY algorithm, edges specify a constituent’s start and end positions, its grammatical category, and its f f f-cost. Here, the g g g component represents the current cost of an edge and the h h h component represents an estimate of the cost to complete a derivation that makes use of that edge. The use of A* for phrase structure parsing originated with (Klein and Manning, 2003a), while the CCG approach presented here is based on (Lewis and Steedman, 2014).
Using information from a supertagger, an agenda and a parse table are initialized with states representing all the possible lexical categories for each word in the input, along with their f f f-costs. The main loop removes the lowest cost edge from the agenda and tests to see if it is a complete derivation. If it reflects a complete derivation it is selected as the best solution and the loop terminates. Otherwise, new states based on the applicable CCG rules are generated, assigned costs, and entered into the agenda to await further processing. The loop continues until a complete derivation is discovered, or the agenda is exhausted, indicating a failed parse. The algorithm is given in Fig. 12.11.
Heuristic Functions
Before we can define a heuristic function for our A* search, we need to decide how to assess the quality of CCG derivations. For the generic PCFG model, we defined the probability of a tree as the product of the probability of the rules that made up the tree. Given CCG’s lexical nature, we’ll make the simplifying assumption that the probability of a CCG derivation is just the product of the probability of the supertags assigned to the words in the derivation, ignoring the rules used in the derivation.
More formally, given a sentence S S S and derivation D D D that contains suptertag sequence T T T , we have:
P ( D , S ) = P ( T , S ) = ∏ i = 1 n P ( t i ∣ s i ) P(D,S) = P(T,S) = \prod_{i=1}^n P(t_i|s_i) P(D,S)=P(T,S)=i=1∏nP(ti∣si)
To better fit with the traditional A* approach, we’d prefer to have states scored by a cost function where lower is better (i.e., we’re trying to minimize the cost of a derivation). To achieve this, we’ll use negative log probabilities to score derivations; this results in the following equation, which we’ll use to score completed CCG derivations.
− log P ( D , S ) = − log P ( T , S ) = ∑ i = 1 n − log P ( t i ∣ s i ) -\log P(D,S) = -\log P(T,S) = \sum_{i=1}^n -\log P(t_i|s_i) −logP(D,S)=−logP(T,S)=i=1∑n−logP(ti∣si)
Given this model, we can define our f f f-cost as follows. The f f f-cost of an edge is the sum of two components: g ( n ) g(n) g(n), the cost of the span represented by the edge, and h ( n ) h(n) h(n), the estimate of the cost to complete a derivation containing that edge (these are often referred to as the inside and outside costs). We’ll define g ( n ) g(n) g(n) for an edge using Equation 30. That is, it is just the sum of the costs of the supertags that comprise the span.
For h ( n ) h(n) h(n), we need a score that approximates but never overestimates the actual cost of the final derivation. A simple heuristic that meets this requirement assumes that each of the words in the outside span will be assigned its most probable supertag. If these are the tags used in the final derivation, then its score will equal the heuristic. If any other tags are used in the final derivation the f f f-cost will be higher since the new tags must have higher costs, thus guaranteeing that we will not overestimate.
Putting this all together, we arrive at the following definition of a suitable f f f-cost for an edge.
f ( w i , j , t i , j ) = g ( w i , j ) + h ( w i , j ) = ∑ k = i j − log P ( t k ∣ w k ) + ∑ k = 1 i − 1 max t ∈ t a g s ( − log P ( t ∣ w k ) ) + ∑ k = j + 1 N max t ∈ t a g s ( − log P ( t ∣ w k ) ) f(w_{i,j},t_{i,j})=g(w_{i,j})+h(w_{i,j})\\ =\sum_{k=i}^j-\log P(t_k|w_k) +\sum_{k=1}^{i-1}\max_{t\in tags}(-\log P(t|w_k))+\sum_{k=j+1}^N\max_{t\in tags}(-\log P(t|w_k)) f(wi,j,ti,j)=g(wi,j)+h(wi,j)=k=i∑j−logP(tk∣wk)+k=1∑i−1t∈tagsmax(−logP(t∣wk))+k=j+1∑Nt∈tagsmax(−logP(t∣wk))
As an example, consider an edge representing the word serves with the supertag N N N in the following example.
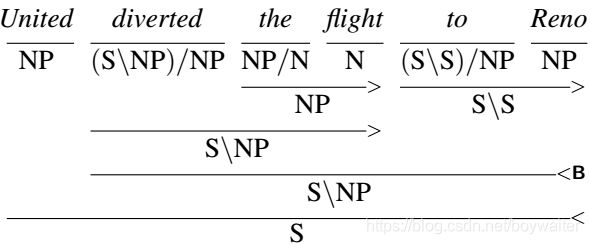
(12.41) United serves Denver.
The g g g-cost for this edge is just the negative log probability of the tag, or X. The outside h h h-cost consists of the most optimistic supertag assignments for United and Denver. The resulting f f f-cost for this edge is therefore x+y+z = 1.494.
An Example
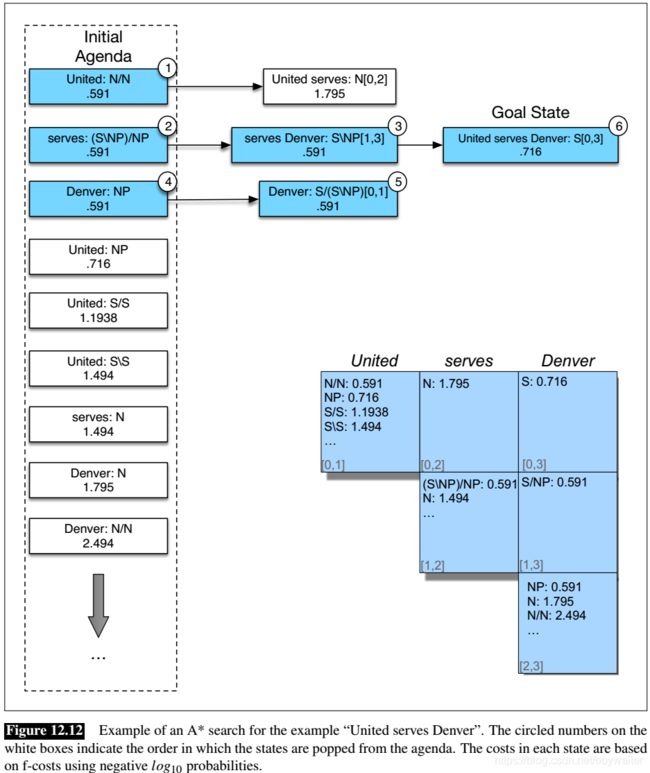
Fig. 12.12 shows the initial agenda and the progress of a complete parse for this example. After initializing the agenda and the parse table with information from the supertagger, it selects the best edge from the agenda — the entry for United with the tag N / N N/N N/N and f f f-cost 0.591. This edge does not constitute a complete parse and is therefore used to generate new states by applying all the relevant grammar rules. In this case, applying forward application to United: N/N and serves: N results in the creation of the edge United serves: N[0,2], 1.795 to the agenda.
Skipping ahead, at the the third iteration an edge representing the complete derivation United serves Denver, S[0,3], .716 is added to the agenda. However, the algorithm does not terminate at this point since the cost of this edge (.716) does not place it at the top of the agenda. Instead, the edge representing Denver with the category NP is popped. This leads to the addition of another edge to the agenda (type-raising Denver). Only after this edge is popped and dealt with does the earlier state representing a complete derivation rise to the top of the agenda where it is popped, goal tested, and returned as a solution.
The effectiveness of the A* approach is reflected in the coloring of the states in Fig. 12.12 as well as the final parsing table. The edges shown in blue (including all the initial lexical category assignments not explicitly shown) reflect states in the search space that never made it to the top of the agenda and, therefore, never contributed any edges to the final table. This is in contrast to the PCKY approach where the parser systematically fills the parse table with all possible constituents for all possible spans in the input, filling the table with myriad constituents that do not contribute to the final analysis.
12.8 Evaluating Parsers
The standard techniques for evaluating parsers and grammars are called the PARSEVAL measures. The intuition of the PARSEVAL metric is to measure how much the constituents in the hypothesis parse tree look like the constituents in a hand-labeled, gold-reference parse. PARSEVAL thus assumes we have a human-labeled “gold standard” parse tree for each sentence in the test set; we generally draw these gold-standard parses from a treebank like the Penn Treebank.
Given these gold-standard reference parses for a test set, a given constituent in a hypothesis parse C h C_h Ch of a sentence s s s is labeled “correct” if there is a constituent in the reference parse C r C_r Cr with the same starting point, ending point, and non-terminal symbol.
We can then measure the precision and recall just as we did for chunking in the previous chapter.
labeled recall: = # of correct constituents in hypothesis parse of s # of correct constituents in reference parse of s \textbf{labeled recall:}= \frac{\verb|#|\textrm{ of correct constituents in hypothesis parse of }s}{\verb|#|\textrm{ of correct constituents in reference parse of }s} labeled recall:=# of correct constituents in reference parse of s# of correct constituents in hypothesis parse of s
lbeled precision: = # of correct constituents in hypothesis parse of s # of total constituents in hypothesis parse of s \textbf{lbeled precision:} =\frac{\verb|#|\textrm{ of correct constituents in hypothesis parse of }s}{\verb|#|\textrm{ of total constituents in hypothesis parse of }s} lbeled precision:=# of total constituents in hypothesis parse of s# of correct constituents in hypothesis parse of s
As with other uses of precision and recall, instead of reporting them separately, F-measure we often report a single number, the F-measure (van Rijsbergen, 1975).
We additionally use a new metric, crossing brackets, for each sentence s:
cross-brackets: the number of constituents for which the reference parse has a bracketing such as ((A B) C) but the hypothesis parse has a bracketing such as (A (B C)).
For comparing parsers that use different grammars, the PARSEVAL metric includes a canonicalization algorithm for removing information likely to be grammarspecific (auxiliaries, pre-infinitival “to”, etc.) and for computing a simplified score (Black et al., 1991). The canonical implementation of the PARSEVAL metrics is called evalb (Sekine and Collins, 1997).
Nonetheless, phrasal constituents are not always an appropriate unit for parser evaluation. In lexically-oriented grammars, such as CCG and LFG, the ultimate goal is to extract the appropriate predicate-argument relations or grammatical dependencies, rather than a specific derivation. Such relations are also more directly relevant to further semantic processing. For these purposes, we can use alternative evaluation metrics based on measuring the precision and recall of labeled dependencies, where the labels indicate the grammatical relations (Lin 1995, Carroll et al. 1998, Collins et al. 1999).
The reason we use components is that it gives us a more fine-grained metric. This is especially true for long sentences, where most parsers don’t get a perfect parse. If we just measured sentence accuracy, we wouldn’t be able to distinguish between a parse that got most of the parts wrong and one that just got one part wrong.
12.9 Human Parsing
Are the kinds of probabilistic parsing models we have been discussing also used by humans when they are parsing? The answer to this question lies in a field called human sentence processing. Recent studies suggest that there are at least two ways in which humans apply probabilistic parsing algorithms, although there is still disagreement on the details.
One family of studies has shown that when humans read, the predictability of a word seems to influence the reading time; more predictable words are read more quickly.
The second family of studies has examined how humans disambiguate sentences that have multiple possible parses, suggesting that humans prefer whichever parse is more probable. These studies often rely on a specific class of temporarily ambiguous sentences called garden-path sentences. These sentences, first described by Bever (1970), are sentences that are cleverly constructed to have three properties that combine to make them very difficult for people to parse:
- They are temporarily ambiguous: The sentence is unambiguous, but its initial portion is ambiguous.
- One of the two or more parses in the initial portion is somehow preferable to the human parsing mechanism.
- But the dispreferred parse is the correct one for the sentence.
The result of these three properties is that people are “led down the garden path” toward the incorrect parse and then are confused when they realize it’s the wrong one. Sometimes this confusion is quite conscious, as in Bever’s example: The horse raced past the barn fell.
Other times, the confusion caused by a garden-path sentence is so subtle that it can only be measured by a slight increase in reading time. The example: The student forgot the solution was in the back of the book.
12.10 Summary
This chapter has sketched the basics of probabilistic parsing, concentrating on probabilistic context-free grammars and probabilistic lexicalized context-free grammars.
- Probabilistic grammars assign a probability to a sentence or string of words while attempting to capture more sophisticated syntactic information than the N-gram grammars of Chapter 3.
- A probabilistic context-free grammar (PCFG) is a context-free grammar in which every rule is annotated with the probability of that rule being chosen. Each PCFG rule is treated as if it were conditionally independent; thus, the probability of a sentence is computed by multiplying the probabilities of each rule in the parse of the sentence.
- The probabilistic CKY (Cocke-Kasami-Younger) algorithm is a probabilistic version of the CKY parsing algorithm. There are also probabilistic versions of other parsers like the Earley algorithm.
- PCFG probabilities can be learned by counting in a parsed corpus or by parsing a corpus. The inside-outside algorithm is a way of dealing with the fact that the sentences being parsed are ambiguous.
- Raw PCFGs suffer from poor independence assumptions among rules and lack of sensitivity to lexical dependencies.
- One way to deal with this problem is to split and merge non-terminals (automatically or by hand).
- Probabilistic lexicalized CFGs are another solution to this problem in which the basic PCFG model is augmented with a lexical head for each rule. The probability of a rule can then be conditioned on the lexical head or nearby heads.
- Parsers for lexicalized PCFGs (like the Charniak and Collins parsers) are based on extensions to probabilistic CKY parsing.
- Parsers are evaluated with three metrics: labeled recall, labeled precision, and cross-brackets.
- Evidence from garden-path sentences and other on-line sentence-processing experiments suggest that the human parser uses some kinds of probabilistic information about grammar.