用遗传算法解决八皇后问题(也许是最易懂的了）

微信公众号 Yuan的学习笔记
知乎 Yuan的学习笔记

那天在看AIMA(Artificial Intelligence : A Modern Approach人工智能:一种现代的方法Stuart Russell著)看到了一个有趣的问题叫八皇后问题。

八皇后问题的目标是在国际象棋棋盘中放置8个皇后，使得任何一个皇后都不会攻击到其他任一皇后。(皇后可以攻击和它在同一行，同一列或者同一对角线的任何棋子)，我把这个问题抛给了周围朋友，纷纷拿起纸笔或打开电脑上的EXCEL表格试了起来，看似简单但都没解决，其中一位还把这个当成了上厕所时的消遣工具

在64个格子的国际象棋棋盘上放置8个棋子有

种放置方法，单纯用手试(还真没找到啥技巧)或计算机穷举都不是好办法，书中介绍了几种算法，但我觉得最有趣的是下面要说的遗传算法。

达尔文的进化论

资料说，遗传算法(Genetic Algorithm，GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。

还记得高中生物课讲的达尔文生物进化论的自然选择，孟德尔豌豆实验和遗传学DNA双螺旋结构吗？进化论(1859)中说变化会出现在繁殖过程中，并且在后代繁衍过程中以一定比例保存下来；Gregor Mendel修道士(1866)在豌豆身上做了实验，掌握了遗传的统计规律；Watson和Crick(1953)确定了DNA分子的结构和它的序列。在有性生殖中后代是由多个而不是一个生物体产生的。而实际的进化机制比多数遗传算法要丰富的多。例如，变异包括DNA的反转，复制和大段移动；一些病毒借用一个生物体的DNA再插入到其他生物体的DNA里。

遗传算法和进化论

我们再来看看遗传算法，首先是一种可能的八皇后的状态

上面这幅图可以用一段序列表示：1 5 8 6 3 7 2 4，代表8个皇后的位置，第1行第1个位置，第2行第5个位置，第3行第8个位置……第8行第4个位置

遗传算法从k个随机生成的状态开始，我们称之为种群Population。每个状态或个体，用一个有限长度的字符串表示.图a显示了4个表示八皇后状态的8位数字串组成的种群

遗传算法通过把两个双亲结合来生成后继，图b到e显示了产生下一代状态的过程。

在b中，每个状态都由它的目标函数或适应度函数给出评估值。对于好的状态，适应度函数会返回较高的值，所以在八皇后问题中，我们用不相互攻击的皇后对的数目来表示，最优解的适应度是28(检查每一个皇后与棋盘上另一个皇后是否冲突需要7+6+5+4+3+2+1=28)。在遗传算法中，被选择进行繁殖的概率直接与个体的适应度成正比，百分比在适应度旁边。

在c中，按照b中的概率随机选择两对进行繁殖，个体可能会被选择多次也可能一次都没有被选中。对于要配对的每对个体，在字符串中随机选择一个位置作为杂交点。

在d中，父串在杂交点上进行杂交而创造出后代。例如，第一对的第一个后代从第一个父串那里得到了前三位数字，从第二个父串那里得到了后五位数字。

最后，每个位置都会按照某个小的独立概率随机变异。在第1，第3和第4个后代中都有一个数字发生了变异。

这样就是由初始第一代到第二代的过程，第二代个体通过适应度函数，选择配对后有性生殖，交叉互换，基因突变，又生成了第三代，不断重复这个过程直到有一代中出现了适应度为28(任意两对8皇后都不冲突)就找到了八皇后问题的解

想的形象些，把每一个初始随机生成的八皇后当成种群内的个体(像是自然界中的动物)，这些个体在环境是否有优势的标准就是谁更接近目标状态的八皇后，用适应度函数来打分，优势越大就越能争取到交配权，从而把自己的优良性状传递下去，而适应度低的个体则有很大概率被淘汰，在有性生殖过程中，双亲交换自己序列的片段，把各自好的状态继承给下一代，如果单纯这样的话，会发现最后种群内个体的序列几乎会变成一样的(后面程序模拟的确会这样)，所以还需要基因突变，就像自然界中基因突变会产生有害的性状但也会产生更加能适应环境的性状，而这些好的基因突变因为在适应度函数评分时可以得到更高的分数，因此又有更大概率将自己的序列遗传给下一代，这样子代渐渐比父代更能适合环境(对应后代八皇后比前代互相间冲突更小)，直到某一子代出现了完全满足条件的八皇后(天选之子)。

用Python代码模拟一下

Fitness function 适应度函数

def fitness_function(individual):
    value = 0
    for i in range(7):
        for j in range(i+1,8,1):
            if individual[i] != individual[j]:
                x_distance = np.abs(individual[j] - individual[i])
                y_distance = j - i
                if x_distance != y_distance:
                    value += 1
    return value

Softmax function 用于把适应度函数转化为概率分布

def softmax(input):
    input = np.array(input, dtype=np.float)
    input = np.exp(input)
    output = input / input.sum()
    return output

Mutation 随机变异

def mutation(individual, prob=0.1):
    p = np.random.rand(8)
    individual[p>prob] = np.random.choice(range(8), 8)[p>prob]

    return individual

GA函数Genetic Algorithm

def GA(size = 4):
    #默认种群大小为4，可以多试几个，效果不一样
    size = size
    num_generation = 0
    population = []
    for i in range(size):
        population.append(np.random.choice(range(8), 8))
    while (True):
        print("Generation : ", num_generation)
        fitness_list = []
        selection = []

        for individual in population:
            fitness_value = fitness_function(individual)
            if fitness_value == 28:
                print("Find Target!")
                print(individual)
                return individual
            fitness_list.append(fitness_value)

        print(fitness_list)
        print()

        #Selection is Here自然选择在这里
        prob = softmax(fitness_list)
        select_id = np.random.choice(range(size), size, replace=True, p=prob)
        for idx in select_id:
            selection.append(population[idx])
        num_pair = int(size/2)
        position = np.random.choice(range(1,7,1), num_pair, replace=True)


        #Crossover is Here基因片段的交叉互换在这里
        for i in range(0, size, 2):
            start = position[int(i/2)]
            tempa = copy.deepcopy(selection[i][start:])
            tempb = copy.deepcopy(selection[i+1][start:])
            selection[i][start:] = tempb
            selection[i+1][start:] = tempa


        #Mutation is Here变异在这里
        for i in range(size):
            selection[i] = copy.deepcopy(mutation(selection[i], prob=0.8))
        population = selection
        num_generation += 1

来看看结果吧
设置初始种群数量为4

Queen = GA(size = 4)

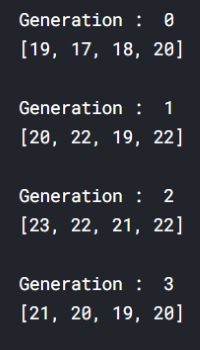
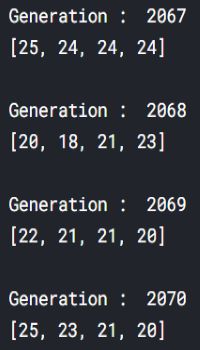
我猜你应该发现了后四代种群的适应度要高于前四代，说明父代适应度更好的状态和有利的突变会大概率传递给子代。在第2071子代最后找到了满足条件的八皇后的解

你猜有多少种

要问有多少种放置方法，我自己通过更改种群大小和随机数，找到了几十种。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解。

当然不只是解决八皇后的

遗传算法在最优化问题上有广泛的影响，如电路布局和作业车调度问题。目前，还不清楚遗传算法的吸引力是源自它们的性能，还是源自它们出身进化理论。很多研究工作正在进行中，分析在什么情况下使用遗传算法能够达到好的效果。

最后感谢一下各位亲朋好友的建议，代码我放在了kaggle，感兴趣的小伙伴可以直接云端运行

https://www.kaggle.com/qiyuange/eight-queens-puzzle/comments#genetic-algorithm-(GA)

参考资料
Artificial Intelligence : A Modern Approach

—完—

分享学习的知识和前沿的事物，希望这个笔记成为你和我的终身学习平台，一起成长一起进步

微信公众号 Yuan的学习笔记
知乎 Yuan的学习笔记