程序员的自我修养-算法递归
程序员的自我修养-算法递归
文章目录
- 程序员的自我修养-算法递归
-
- 1 递归概念引入
-
- 1.1 来举一个简单的例子
- 1.2 递归的一些必要条件
- 2 如何使用递归
-
- 爬楼梯问题
- 括号生成问题
- 组合问题
- 路径计数问题
- 3 递归的效率问题
- 总结
- 参考文档
1 递归概念引入
首先,思考一个小小的问题,计算机 是如何解决问题的?在计算机的世界里面 只有简单的
if else , for loop , while ,do while , recursion 等这些简单的指令集,计算机 是一个没有感情的机器,计算机更加喜欢 做的事情 是什么呢?
就是 重复性的问题,计算机特别擅长。
所以 递归(recursion ) 就诞生了,所以 递归是什么呢? 递归就是自己调用自己的一个过程,是一种编程的技巧。
1.1 来举一个简单的例子
比如现在 我要计算 1 + 2 + … 100 ,举一个不是特别恰当的例子,假设 我现在有一个函数 可以从50 到100 计算和, 那么我只需要计算 1到50 的和,然后调用另外一个函数 计算 结果,然后把结果加起来。
def sum_to_hundred():
"""
计算 1 + 2 + ... 100
:return:
"""
r = 0
for i in range(1, 50):
r += i
r2 = sum_50_100()
return r + r2
def sum_50_100():
"""
计算 50 到100 的和
:return:
"""
sum = 0
for i in range(50, 101):
sum += i
return sum
if __name__ == '__main__':
r = sum_to_hundred()
print(r)
例子 应该比较简单,但是我们应该思考 一个问题, 1 + 2 + 3 …+98+ 99+ 100 这个问题 会有一些自相似性。
换个角度想一想,如果我要计算1 + 2 + 3 …+ 98+ 99 + 100 的和,
如果是可以知道假设 1 + 2 + 3 …+98+ 99 = X ,上面的式子 X + 100
如果是可以知道假设 1 + 2 + 3 …+98 = Y ,上面的式子 Y + 99 + 100
如果是可以知道假设 1 + 2 + 3 …+97 = Z ,上面的式子 Z + 98 + 99 + 100
…
那么我们知道什么,很简单啊,
1 = XXX 等于 1 ,这里就是找了最初的结果。 所以我们尝试 用递归的方式 来实现一下 这个函数。
def recur(n=100):
# base case
if n == 1:
return 1
return recur(n - 1) + n
这里我定义 recur(n) 表示的 从 [1,n] 的和.
recur(5)
recur(4) + 5
(recur(3) + 4) + 5
((recur(2) + 3)+ 4) + 5
(( (recur(1) + 2) + 3) + 4) + 5
因为 recur(1) 的结果我们 很清楚啊,就是1 ,所以计算机 就把 1 +2 +…+ 5 的结果 计算出来了。
1.2 递归的一些必要条件
思考一下 递归需要哪些 必要的条件
-
base case 就是 基线 的条件
-
递归条件
递归的基线条件 就是 何时 结束递归 函数进行返回 上一个例子中, 就是 n==1 ,这个条件 就是基线条件
第二点 递归的递归条件, 递归条件 是如何把 递归往 递归 条件上 改变的条件, 随着递归条件的不断变化,最终 可以到达 基线条件。 上一个求和的例子中 recur(n) = recur(n-1) + n 这个就是递归条件。
我们按照算法时间复杂度的角度 重新思考这个问题, n 相当于问题规模, 递归条件 每次 把问题规模减低到一个 ,最后降到 我们直接就可以看出结果的条件(base case).
好,现在 练手一下,如果 需要算法 n! 请使用递归的方式写出来
首先 思考 : 基线条件是什么? 第二 递归条件是什么 ?
def factorial(n: int) -> int:
if n == 1:
return 1
return factorial(n - 1) * n
2 如何使用递归
刚刚举例子,是比较简单的,这个时候你可能并没有感觉到递归 带来的好处是什么,我举几个稍微复杂的例子,
大家一起思考。
爬楼梯问题
假设小明正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
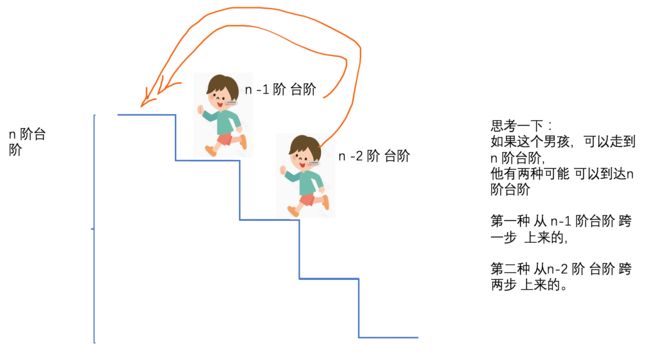
假设小明 现在 在楼梯的开始上楼,
思考一下:
如果 小明 可以跳到 n 阶台阶,则 只有两种方案 可以跳上来。
假设 f(n) 表示 跳到 n 阶台阶的方法数, 那么
f(n) = f(n-1) + f(n-2)
想一想 base case
f(1) = 1
f(2) = 2
那么 比较容易些出来 以下的代码。
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
else:
return self.climbStairs(n-1) + self.climbStairs(n-2)
思考一下 这个 代码有没有什么问题呢?
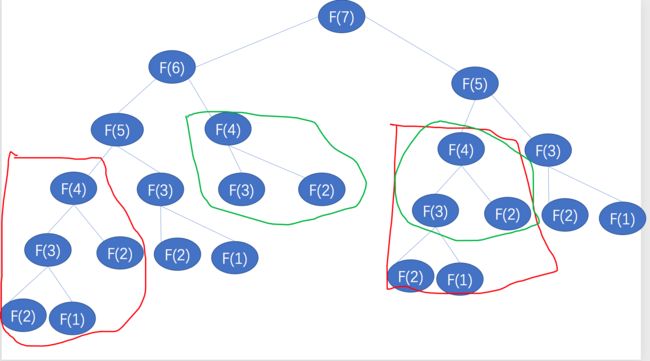
画一下 递归的状态树, 这里 大概画了一下,
我们 从一下 可以看出 递归的状态 有大量的重复计算的问题。 如何解决这个问题呢?
其中 红色部分,绿色部分 都进行了重复的计算,所以可以把计算的结果 先保存起来,如果发现这个值已经计算过了,直接使用之前计算过的值即可。
优化后的代码:
把重复计算的结果 保存起来
class Solution:
memo = dict()
def climbStairs(self, n: int) -> int:
if n in self.__class__.memo:
return self.__class__.memo[n]
if n <= 2:
self.__class__.memo[n] = n
else:
r = self.climbStairs(n - 1) + self.climbStairs(n - 2)
self.__class__.memo[n] = r
return self.__class__.memo[n]
使用内置的 lru_cache 进行缓存 就行, 不用自己手写 lru_cache
from functools import lru_cache
class Solution:
@lru_cache(maxsize=128)
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
else:
return self.climbStairs(n-1) + self.climbStairs(n-2)
更好的解法 dp 法
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
括号生成问题
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
有效括号的含义 是指 是一个成对出现的括号, 是一个合法的括号的表达方式, 就如上面的例子。
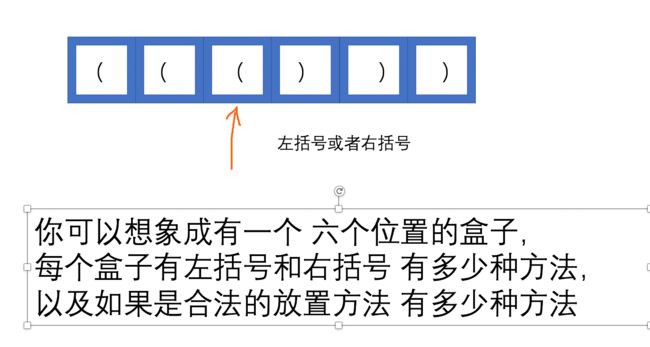
假设 n = 3 这种情况,
先假设 没有要求括号合法性的要求
from typing import List
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
max_level = 2*n
level = 0
cur_result = ""
self._generate(max_level=max_level,level=level,cur_result=cur_result)
def _generate(self,max_level,level, cur_result):
# terminator
if level == max_level:
print(cur_result)
# notice
return
# current logic ,and drill down next level
self._generate(max_level,level+1,cur_result+"(")
self._generate(max_level,level+1,cur_result+")")
# reverse current level status
pass
加上如何检查 括号的合法性的逻辑
其实递归的过程中,我们可以检查 一些不合法的括号,直接 停止递归就好了。
对于左括号,如果括号没有用完,就可以直接添加。
对于右括号, 要保证 左括号的了数量> 右括号的数量,就可以继续添加了。
from typing import List
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
max_level = n
cur_result = ""
left,right = 0,0
self.result = []
self._generate(max_level=max_level, left=left,right=right,cur_result=cur_result)
return self.result
def _generate(self,max_level,left,right, cur_result):
# terminator
if left == max_level and right == max_level:
# print(cur_result)
self.result.append(cur_result)
# notice
return
# current logic ,and drill down
if left < max_level:
self._generate(max_level,left+1,right,cur_result+"(")
if left > right:
self._generate(max_level, left, right + 1, cur_result + ")")
# reverse current level status
pass
这里 有一个模板尝试找一些题目进行练习。
# python
def recursion(level, param1, param2, ...):
# recursion terminator
if level > MAX_LEVEL:
process_result
return
# process logic in current level
process(level, data...)
# drill down
self.recursion(level + 1, p1, ...)
# reverse the current level status if needed
# pass
组合问题
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
- 回溯算法
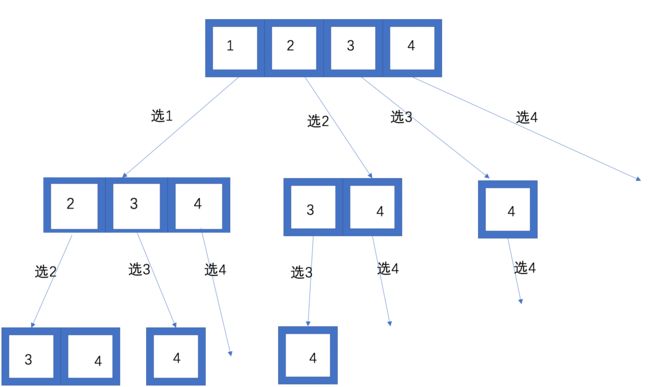
思考一下 如何求解:
其实 只要吧转态树画出来 理解一下,就相对 简单一点。 当从 取出一个数后,之后 就不能取相同的数字,
所以 怎么控制取不到相同的数字呢?
想一想 递归的 基线条件是什么?
是不是递归的深度 level 等于 k 的时候,
每次递归的下一层的时候, 要从没有取到数开始 取,不能取到之前的数字,所以需要在递归 的时候 给一个 参数代表 当前层的开始的位置在哪里呢? 这里我命名为 start 代表下一层开始的数字。
from typing import List
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
level = 0
start = 1
cur_result = []
self.result = []
self._generate(n, k, level=level, start=start, cur_result=cur_result)
return self.result
def _generate(self, n, k, level, start, cur_result:List):
# terminator
if level == k:
self.result.append(cur_result.copy())
return
# currrent logic process and drill down
for i in range(start, n + 1):
cur_result.append(i)
self._generate(n, k, level + 1, start=i + 1, cur_result=cur_result)
# reverse current level states
cur_result.pop(-1)
if __name__ == '__main__':
r = Solution().combine(n=4, k=2)
print(r)
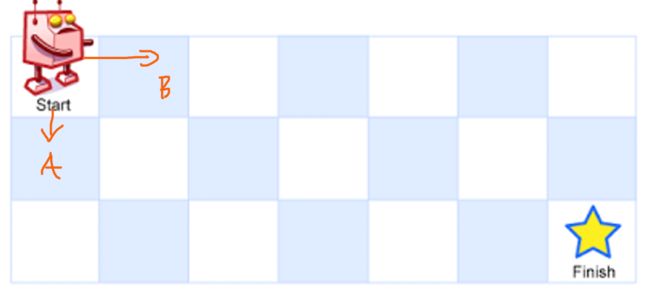
路径计数问题
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
![]()
例如,上图是一个7 x 3 的网格。有多少可能的路径?
示例 1:
输入: m = 3, n = 2 输出: 3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向右 -> 向下 2. 向右 -> 向下 -> 向右 3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3 输出: 28
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10 ^ 9
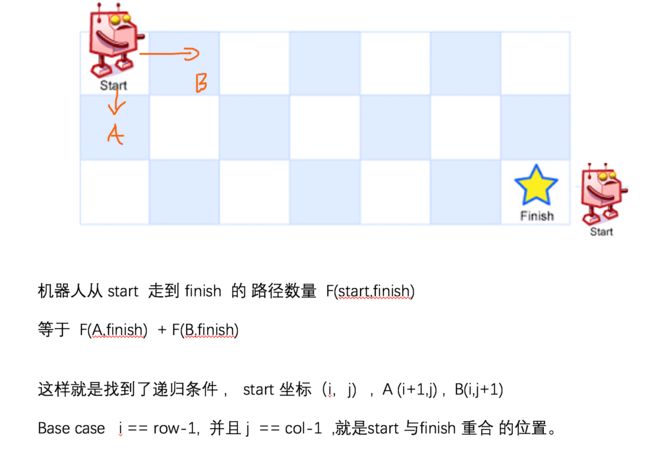
由于机器人只能 向右 或者向下 走 。 这样就走到了重复 子问题了。
递归的写法
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
i, j = 0, 0
r = self.count_path(m, n, i, j)
return r
def count_path(self, row, col, i, j):
# terminator
if i >= row or j >= col:
return 0
if i == row-1 and j == col-1:
# find a result
return 1
return self.count_path(row, col, i + 1, j) + self.count_path(row, col, i, j + 1)
记忆化搜索 可以把结果存起来
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
i, j = 0, 0
self.memo = dict()
r = self.count_path(m, n, i, j)
return r
def count_path(self, row, col, i, j):
if (i,j) in self.memo:
return self.memo.get((i,j))
# terminator
if i >= row or j >= col:
self.memo[(i, j)] = 0
return self.memo[(i, j)]
if i == row-1 and j == col-1:
self.memo[(i, j)] = 1
return self.memo[(i, j)]
self.memo[(i, j)] = self.count_path(row, col, i + 1, j) + self.count_path(row, col, i, j + 1)
return self.memo[(i,j)]
有没有 更好的办法? 可以自行思考一下.
3 递归的效率问题
递归 有哪些 问题呢?
效率对比
递归的话,需要额外的栈的空间开销,这个需要一定空间成本的。 对于for 循环 就 不太需要,直接循环,不需要 额外的栈空间。
def recur(n=100):
if n == 1:
return 1
return recur(n - 1) + n
def my_sum(n):
_sum = 0
for i in range(n):
_sum += i
return _sum
if __name__ == '__main__':
n = 500
start = time.time()
print(my_sum(n=n))
print(f"my_sum totoal time :{time.time() - start}")
start = time.time()
print(recur(n=n))
print(f"recur totoal time :{time.time() - start}")
pass
总结
递归的关键要点 第一 要找到 最近重复子问题,第二要找base case 基线条件。 然后开始写递归,递归过程中一定不要忘记递归的终止条件。
参考文档
爬楼梯问题
括号生成问题
不同路径
组合
全排列
全排列 II
程序员的自我修养-算法递归-readdocs