leetcode刷题---热门百题---组合总和---回溯算法

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。 

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
[2,2,2,2],
[2,3,3],
[3,5]
]

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500

这题因为要列举出所有可能的情况，所有就要想到回溯算法，和生成括号相同的是有一个隐式的树的结构，下面是题解

题解

对于这类寻找所有可行解的题，我们都可以尝试用「搜索回溯」的方法来解决。

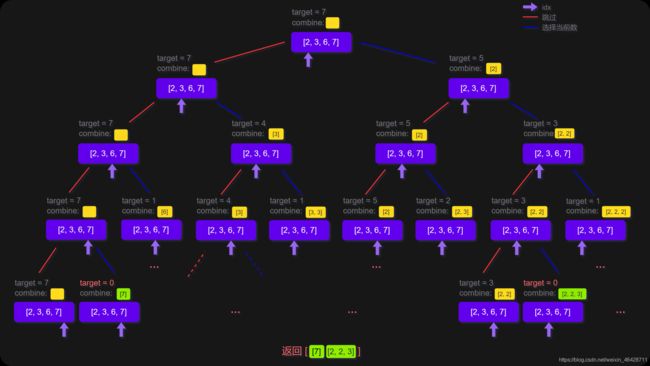
回到本题，我们定义递归函数 dfs(target, combine, idx) 表示当前在 candidates 数组的第 idx 位，还剩 target 要组合，已经组合的列表为 combine。递归的终止条件为 target <= 0 或者 candidates 数组被全部用完。那么在当前的函数中，每次我们可以选择跳过不用第 idx 个数，即执行 dfs(target, combine, idx + 1)。也可以选择使用第 idx 个数，即执行 dfs(target - candidates[idx], combine, idx)，注意到每个数字可以被无限制重复选取，因此搜索的下标仍为 idx。

更形象化地说，如果我们将整个搜索过程用一个树来表达，即如下图呈现，每次的搜索都会延伸出两个分叉，直到递归的终止条件，这样我们就能不重复且不遗漏地找到所有可行解：

class Solution {
     
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
     
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        List<Integer> combine = new ArrayList<Integer>();
        dfs(candidates, target, ans, combine, 0);
        return ans;
    }

    public void dfs(int[] candidates, int target, List<List<Integer>> ans, List<Integer> combine, int idx) {
     
        if (idx == candidates.length) {
     
            return;
        }
        if (target == 0) {
     
            ans.add(new ArrayList<Integer>(combine));
            return;
        }
        // 直接跳过
        dfs(candidates, target, ans, combine, idx + 1);
        // 选择当前数
        if (target - candidates[idx] >= 0) {
     
            combine.add(candidates[idx]);
            dfs(candidates, target - candidates[idx], ans, combine, idx);
            combine.remove(combine.size() - 1);
        }
    }
}


作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/combination-sum/solution/zu-he-zong-he-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/combination-sum/solution/zu-he-zong-he-by-leetcode-solution/
来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。