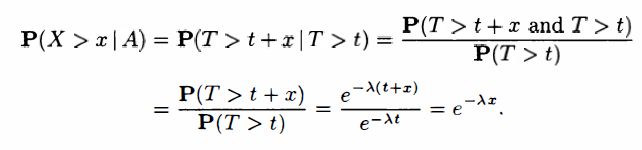Chapter 3 (General Random Variables): Conditioning (条件)

本文为 $Introduction$ $to$ $Probability$ 的读书笔记

Conditioning a Random Variable on an Event

• The conditional PDF of a continuous random variable $X$, given an event $A$ with $P(A)>0$, is defined as a nonnegative function $f_{X|A}$ that satisfies
  $$P(X\in B|A)={\int }_B{f}_{X|A}(x)dx$$for any subset $B$ of the real line. In particular, by letting $B$ be the entire real line, we obtain the normalization property
  $${\int }_{-\infty }^{\infty }{f}_{X|A}(x)dx=1$$
• In the important special case where we condition on an event of the form $\{X\in A\}$, with $P(X\in A)>0$, the definition of conditional probabilities yields
  $$P(X\in B|X\in A)=\frac{P(X\in B,X\in A)}{P(X\in A)}=\frac{{\int }_{A\cap B}{f}_X(x)dx}{P(X\in A)}$$By comparing with the earlier formula, we conclude that
  As in the discrete case, the conditional PDF is zero outside the conditioning set. Within the conditioning set, the conditional PDF has exactly the same shape as the unconditional one, except that it is scaled by the constant factor $1/P(X\in A)$, so that $f_{X|\{X\in A\}}$ integrates to 1; see Fig. 3.14. Thus, the conditional PDF is similar to an ordinary PDF, except that it refers to a new universe in which the event $\{X\in A\}$ is known to have occurred.
  

---

Example 3.13. The Exponential Random Variable is Memoryless.
The time $T$ until a new light bulb burns out is an exponential random variable with parameter $\lambda$. Ariadne turns the light on, leaves the room, and when she returns, $t$ time units later, finds that the light bulb is still on, which corresponds to the event $A=\{T>t\}$. Let $X$ be the additional time until the light bulb burns out. What is the conditional CDF of $X$, given the event $A$?

SOLUTION

---

joint conditional PDF

• Suppose, for example, that $X$ and $Y$ are jointly continuous random variables, with joint PDF $f_{X,Y}$. If we condition on a positive probability event of the form $C=\{(X,Y)\in A\}$, we have
  
• In this case, the conditional PDF of $X$, given this event, can be obtained from the formula
  $$f_{X|C}(x)={\int }_{-\infty }^{\infty }{f}_{X,Y|C}(x,y)dy$$These two formulas provide one possible method for obtaining the conditional PDF of a random variable $X$ when the conditioning event is not of the form $\{X\in A\}$, but is instead defined in terms of multiple random variables.

---

• We finally note that there is a version of the total probability theorem which involves conditional PDFs: if the events $A_1,...,A_n$ form a partition of the sample space, then
  $$f_X(x)=\sum _{i=1}^{n}P(A_i)f_{X|A_i}(x)$$
• To justify this statement, we use the total probability theorem and obtain
  $$P(X\le x)=\sum _{i=1}^{n}P(A_i)P(X\le x|A_i)$$This formula can be rewritten as
  $${\int }_{-\infty }^x{f}_X(t)dt=\sum _{i=1}^{n}P(A_i){\int }_{-\infty }^x{f}_{X|A_i}(t)dt$$We then take the derivative of both sides, with respect to $x$, and obtain the desired result.

---

Example 3.14.
The metro train arrives at the station near your home every quarter hour starting at 6:00 a.m. You walk into the station every morning between 7:10 and 7:30 a.m., and your arrival time is a uniform random variable over this interval. What is the PDF of the time you have to wait for the first train to arrive?

SOLUTION

• Let $X$ be the time of your arrival and $Y$ be the waiting time. We calculate the PDF $f_Y$ using a divide-and-conquer strategy. Let $A$ and $B$ be the events
  
  $$\begin{array}{rl}{f}_Y(y)& =P(A)f_{Y|A}(y)+P(B)f_{Y|B}(y)\end{array}$$
  
• We have
  

Conditioning one Random Variable on Another

• Let $X$ and $Y$ be continuous random variables with joint PDF $f_{X,Y}$. For any $y$ with $f_Y(y)>0$ . the conditional PDF of $X$ given that $Y=y$, is defined by
  $$f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}$$
  

---

• For the case of more than two random variables, there are natural extensions to the above. For example, we can define conditional PDFs by formulas such as
  

---

• To interpret the conditional PDF, let us fix some small positive numbers ${\delta }_1$ and ${\delta }_2$, and condition on the event $B=\{y\le Y\le y+{\delta }_2\}$. We have
  
• In words, $f_{X|Y}(x|y){\delta }_1$ provides us with the probability that $X$ belongs to a small interval $[x,x+{\delta }_1]$, given that $Y$ belongs to a small interval $[y,y+{\delta }_2]$. Since $f_{X|Y}(x|y){\delta }_1$ does not depend on ${\delta }_2$, we can think of the limiting case where ${\delta }_2$ decreases to zero and write
  $$P(x\le X\le x+{\delta }_1|Y=y)\approx f_{X|Y}(x|y){\delta }_1$$and, more generally,
  $$P(X\in A|Y=y)={\int }_A{f}_{X|Y}(x|y)dx$$
• Conditional probabilities are given the zero probability event $\{Y=y\}$. But the above formula provides a natural way of defining such conditional probabilities. In addition, it allows us to view the conditional PDF $f_{X|Y}(x|y)$ (as a function of $x$) as a description of the probability law of $X$, given that the event $\{Y=y\}$ has occurred.

---

Example 3.16.
The speed of a typical vehicle that drives past a police radar is modeled as an exponentially distributed random variable $X$ with mean 50 miles per hour. The police radar’s measurement $Y$ of the vehicle’s speed has an error which is modeled as a normal random variable with zero mean and standard deviation equal to one tenth of the vehicle’s speed. What is the joint PDF of $X$ and $Y$?

SOLUTION

• We have $f_X(x)=(1/50)e^{-x/50}$, for $x\ge 0$. Also, conditioned on $X=x$, the measurement $Y$ has a normal PDF with mean $x$ and variance $x^2/100$. Therefore,
  $$f_{Y|X}(y|x)=\frac{1}{\sqrt{2\pi }(x/10)}{e}^{-(y-x{)}^2/(2x^2/100)}$$Thus, for all $x\ge 0$ and all $y$,
  $$f_{X,Y}(x,y)=f_X(x)f_{Y|X}(y|x)$$

---

Problem 34.
A defective coin minting machine produces coins whose probability of heads is a random variable $P$ with PDF
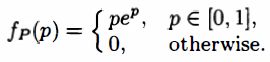A coin produced by this machine is selected and tossed repeatedly, with successive tosses assumed independent. Find the probability that a coin toss results in heads.

SOLUTION

• Let $A$ be the event that the first coin toss resulted in heads. To calculate the probability $P(A)$, we use the continuous version of the total probability theorem:
  $$P(A)={\int }_0^{1}P(A|P=p)f_P(p)dp={\int }_0^1{p}^2{e}^{p}dp=e-2$$

Conditional Expectation

Let $X$ snd $Y$ be jointly continuous random variables, and let $A$ be an event with $P(A)>0$.

• Definitions: The conditional expectation of $X$ given the event $A$ is defined by
  $$E[X|A]={\int }_{-\infty }^{\infty }x{f}_{X|A}(x)dx$$The conditional expectation of $X$ given that $Y=y$ is defined by
  $$E[X|Y=y]={\int }_{-\infty }^{\infty }x{f}_{X|Y}(x|y)dx$$
• The expected value rule: For a function $g(X)$, we have
  $$E[g(X)|A]={\int }_{-\infty }^{\infty }g(x)f_{X|A}(x)dx$$and
  $$E[g(X)|Y=y]={\int }_{-\infty }^{\infty }g(x)f_{X|Y}(x|y)dx$$
• Total expectation theorem: Let $A_1,A_2,...,A_n$ be disjoint events that form a partition of the sample space, and assume that $P(A_i)>0$ for all $i$. Then,
  $$E[X]=\sum _{i=1}^{n}P(A_i)E[X|A_i]$$Similarly,
  $$E[X]={\int }_{-\infty }^{\infty }E[X|Y=y]f_Y(y)dy$$
  • To justify the first version of the total expectation theorem, we start with the total probability theorem
    $$f_X(x)=\sum _{i=1}^{n}P(A_i)f_{X|A_i}(x)$$multiply both sides by $x$, and then integrate from $-\infty$ to $\infty$.
  • To justify the second version of the total expectation theorem, we observe that
    
• There are natural analogs for the case of functions of several random variables. For example,
  $$E[g(X,Y)|Y=y]=\int g(x,y)f_{X|Y}(x|y)dx$$and
  $$E[g(X,Y)]=\int E[g(x,y)|Y=y]f_Y(y)dy$$

---

• The total expectation theorem can often facilitate the calculation of the mean, variance, and other moments of a random variable, using a divide-and-conquer approach.

Example 3.17. Mean and Variance of a Piecewise Constant PDF.

• Suppose that the random variable $X$ has the piecewise constant PDF
  
• Consider the events
  $$\begin{gathered} P(A_1)={\int }_0^1{f}_X(x)dx=\frac{1}{3},P(A_2)={\int }_1^2{f}_X(x)dx=\frac{2}{3} \\ E[X|A_1]={\int }_{-\infty }^{\infty }x{f}_{X|A_1}(x)dx={\int }_0^{1}x\frac{f_X(x)}{P(A_1)}dx={\int }_0^{1}xdx=\frac{1}{2} \\ E[X^2|A_1]={\int }_{-\infty }^{\infty }{x}^2{f}_{X|A_1}(x)dx={\int }_0^1{x}^2\frac{f_X(x)}{P(A_1)}dx={\int }_0^1{x}^{2}dx=\frac{1}{3} \\ E[X|A_2]={\int }_{-\infty }^{\infty }x{f}_{X|A_2}(x)dx={\int }_1^{2}x\frac{f_X(x)}{P(A_2)}dx={\int }_1^{2}xdx=\frac{3}{2} \\ E[X^2|A_1]={\int }_{-\infty }^{\infty }{x}^2{f}_{X|A_1}(x)dx={\int }_1^2{x}^2\frac{f_X(x)}{P(A_1)}dx={\int }_1^2{x}^{2}dx=\frac{7}{3} \end{gathered}$$
• We now use the total expectation theorem to obtain
  $$\begin{gathered} E[X]=P(A_1)E[X|A_1]+P(A_2)E[X|A_2]=\frac{7}{6} \\ E[X^2]=P(A_1)E[X^2|A_1]+P(A_2)E[X^2|A_2]=\frac{15}{9} \end{gathered}$$The variance is given by
  $$var(X)=E[X^2]-(E[X]{)}^2=\frac{11}{36}$$

Independence

• Two continuous random variables $X$ and $Y$ are independent if their joint PDF is the product of the marginal PDFs
  $$f_{X,Y}(x,y)=f_X(x)f_Y(y),forallx,y$$
• There is a natural generalization to the case of more than two random variables. For example, we say that the three random variables $X,Y$, and $Z$ are independent if
  $$f_{X,Y,Z}(x,y,z)=f_X(x)f_Y(y)f_Z(z),forallx,y,z$$
• If $X$ and $Y$ are independent, then any two events of the form $\{X\in A\}$ and $\{Y\in B\}$ are independent
  
• If any two events of the form $\{X\in A\}$ and $\{Y\in B\}$ are independent, then $X$ and $Y$ are independent
  $$\begin{gathered} F_{X,Y}(x,y)=P(X\le x,Y\le y)=P(X\le x)P(Y\le y)=F_X(x)F_Y(y) \\ \therefore f_{X,Y}(x,y)=\frac{{\partial }^2{F}_{X,Y}(x,y)}{\partial x\partial y}=f_X(x)f_Y(y) \end{gathered}$$
• In particular, independence implies that
  $$F_{X,Y}(x,y)=P(X\le x,Y\le y)=P(X\le x)P(Y\le y)=F_X(x)F_Y(y)$$This property can be used to provide a general definition of independence between two random variables. e.g., if $X$ is discrete and $Y$ is continuous.
• An argument similar to the discrete case shows that if $X$ and $Y$ are independent, then
  $$\begin{gathered} E[g(X)h(Y)]=E[g(X)]E[h(Y)] \\ var(X+Y)=var(X)+var(Y) \end{gathered}$$

---

Problem 22.
We have a stick of unit length, and we consider breaking it in three pieces using one of the following three methods. For each of the methods (i), (ii), and (iii), what is the probability that the three pieces we are left with can form a triangle?

• (i) We choose randomly and independently two points on the stick using a uniform PDF, and we break the stick at these two points.
• (ii) We break the stick at a random point chosen by using a uniform PDF, and then we break the piece that contains the right end of the stick, at a random point chosen by using a uniform PDF.
• (iii) We break the stick at a random point chosen by using a uniform PDF, and then we break the larger of the two pieces at a random point chosen by using a uniform PDF.

SOLUTION

• Define coordinates such that the stick extends from position 0 (the left end) to position 1 (the right end). Denote the position of the first break by $X$ and the position of the second break by $Y$. With method (ii), we have $X<Y$. With methods (i) and (iii), we assume that $X<Y$ and we later account for the case $Y<X$ by using symmetry.
• Under the assumption $X<Y$, the three pieces form a triangle if
  $$\begin{gathered} X<(Y-X)+(1-Y) \\ (Y-X)<X+(1-Y) \\ (1-Y)<X+(Y-X) \end{gathered}$$These conditions simplify to
  $$X<0.5;Y>0.5;Y-X<0.5$$
• Consider first method (i). For $X$ and $Y$ to satisfy these conditions, the pair $(X,Y)$ must lie within the triangle with vertices $(0,0.5),(0.5,0.5)$, and $(0.5,1)$. This triangle has area $1/8$. Thus the probability of the event that the three pieces form a triangle $and$ $X<Y$ is $1/8$. By symmetry, the probability of the event that the three pieces form a triangle and $X>Y$ is $1/8$. Since there two events are disjoint and form a partition of the event that the three pieces form a triangle, the desired probability is $1/4$.
• Consider next method (ii). Since $X$ is uniformly distributed on $[0,1]$ and $Y$ is uniformly distributed on $[X,1]$, we have for $0\le x\le y\le 1$,
  $$f_{X,Y}(x,y)=f_X(x)f_{Y|X}(y|x)=1\cdot \frac{1}{1-x}$$The desired probability is the probability of the triangle with vertices $(0,0.5),(0.5,0.5)$, and $(0.5,1)$:
  
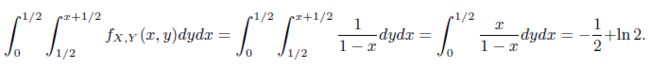
• Consider finally method (iii). Consider first the case $X<0.5$. Then the larger piece after the first break is the piece on the right. Thus, as in method (ii), $Y$ is uniformly distributed on $[X,1]$ and the integral above gives the probability of a triangle being formed $and$ $X<0.5$. Considering also the case $X>0.5$ doubles the probability, giving a final answer of $-1+2ln2$

---

Problem 30. The Beta PDF.

• The beta PDF with parameters $\alpha >0$ and $\beta >0$ has the form
  
• The normalizing constant is
  $$B(\alpha ,\beta )={\int }_0^1{x}^{\alpha -1}(1-x{)}^{\beta -1}dx,$$and is known as the Beta function.
• (a) Show that for any $m>0$, the $m$th moment of $X$ is given by
  $$E[X^m]=\frac{B(\alpha +m,\beta )}{B(\alpha ,\beta )}$$
• (b) Assume that $\alpha$ and $\beta$ are integer. Show that
  $$B(\alpha ,\beta )=\frac{(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}$$so that
  $$E[X^m]=\frac{\alpha (\alpha +1)...(\alpha +m-1)}{(\alpha +\beta )(\alpha +\beta +1)...(\alpha +\beta +m-1)}$$

SOLUTION
(b)

• In the special case where $\alpha =1$ or $\beta =1$, we can carry out the straightforward integration in the definition of $B(\alpha ,\beta )$, and verify the result.
• We will now deal with the general case. Let $Y,Y_1,...,Y_{\alpha +\beta }$ be independent random variables, uniformly distributed over the interval $[0,1]$, and let $A$ be the event
  $$A=\{Y_1\le ...\le Y_{\alpha }\le Y\le Y_{\alpha +1}\le ...\le Y_{\alpha +\beta }\}$$Then
  $$P(A)=\frac{1}{(\alpha +\beta +1)!}$$because all ways of ordering these $\alpha +\beta +1$ random variables are equally likely.
• Consider the following two events:
  $$\begin{gathered} B=\{max\{Y_1,...,Y_{\alpha }\}\le Y\} \\ C=\{Y\le min\{Y_{\alpha +1},...,Y_{\alpha +\beta }\}\} \end{gathered}$$We have, using the total probability theorem,
  $$\begin{array}{rl}P(B\cap C)& ={\int }_0^{1}P(B\cap C|Y=y)f_Y(y)dy\\ & ={\int }_0^{1}P(max\{Y_1,...,Y_{\alpha }\}\le y\le min\{Y_{\alpha +1},...,Y_{\alpha +\beta }\})dy\\ & ={\int }_0^{1}P(max\{Y_1,...,Y_{\alpha }\}\le y)P(y\le min\{Y_{\alpha +1},...,Y_{\alpha +\beta }\})dy\\ & ={\int }_0^1{y}^{\alpha }(1-y{)}^{\beta }dy\end{array}$$
• We also have
  $$P(A|B\cap C)=\frac{1}{\alpha !\beta !}$$because given the events $B$ and $C$, all $\alpha !$ possible orderings of $Y_1,...,Y_{\alpha }$ are equally likely, and all $\beta !$ possible orderings of $Y_{\alpha +1},...,Y_{\alpha +\beta }$ are equally likely.
• By writing the equation
  $$P(A)=P(B\cap C)P(A|B\cap C)$$in terms of the preceding relations, we finally obtain
  $$B(\alpha ,\beta )={\int }_0^1{x}^{\alpha -1}(1-x{)}^{\beta -1}dx=\frac{(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}$$

---