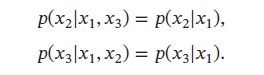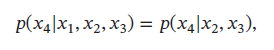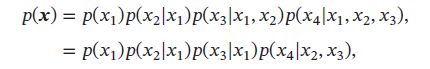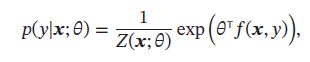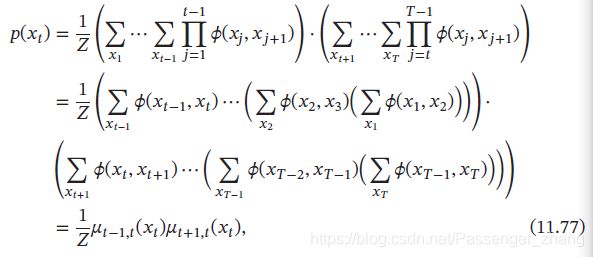《神经网络与深度学习》-概率图模型
概率图模型
-
- 1. 模型的表示
-
- 1.1 有向图模型
- 1.2 常见的有向图模型
-
- 1.2.1 Sigmoid信念网络
- 1.2.2 朴素贝叶斯分类器
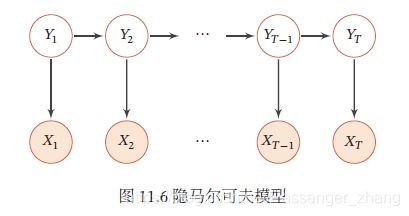
- 1.2.3 隐马尔科夫模型
- 1.3 无向图模型
- 1.4 无向图模型的概率分解
- 1.5 常见的无向图模型
-
- 1.5.1 对数线性模型
- 1.5.2 条件随机场
- 1.6 有向图和无向图之间的转换
- 2. 学习
-
- 2.1 不含隐变量的参数估计
- 2.2 含隐变量的参数估计
-
- 2.2.1 EM算法
- 2.2.2 高斯混合模型
- 3. 推断
-
- 3.1 精确推断
-
- 3.1.1 变量消除法
- 3.1.2 信念传播算法
- 3.2 近似推断
- 4. 近似推断-变分推断
- 5. 基于采样法的近似推断
-
- 5.1 采样法
- 5.2 拒绝采样
- 5.3 重要性采样
- 5.4 马尔科夫链蒙特卡罗方法
-
- 5.4.1 Metropolis-Hastings 算法
- 5.4.2 Metropolis 算法
- 5.4.3 吉布斯采样
- 6. 总结
概率图模型,简称 图模型,是指用图结构来描述多元随机变量之间条件独立关系的概率模型,从而给研究高维空间的概率模型带来便捷性。
对于一个K维随机变量 X = [ X 1 , X 2 , ⋯ , X k ] \pmb{X}=[X_1, X_2,\cdots,X_k] XXX=[X1,X2,⋯,Xk] ,其联合概率为高维空间中的分布,一般难以直接建模,假设每个变量为离散变量并有M个取值,在不作任何独立假设条件下,则需要 M K − 1 M^K-1 MK−1个参数才能表示其概率分布,当 M = 2 , K = 100 M=2,K=100 M=2,K=100时,参数量约为 1 0 30 10^{30} 1030,远超当前计算机储存能力。
一种有效减少参数量的方法是独立性假设,一个K随机变量 X \pmb{X} XXX的联合概率分解为K个条件概率的乘积:
其中, x k x_k xk表示变量 X k X_k Xk的取值,如果某些变量之间存在条件独立性,其参数量就可以大幅减少
假设四个二值变量 X 1 , X 2 , X 3 , X 4 X_1, X_2, X_3, X_4 X1,X2,X3,X4,在不知道这几个变量依赖关系的情况下,可用一个联合概率表来记录每一种取值的概率 p ( x 1 : 4 ) p(\pmb{x}_{1:4}) p(xxx1:4),共需要 2 4 − 1 = 15 2^4-1=15 24−1=15个参数,假设已知 X 1 X_1 X1, X 2 X_2 X2和 X 3 X_3 X3独立,即有:
在已知 X 2 X_2 X2和 X 3 X_3 X3时, X 4 X_4 X4和 X 1 X_1 X1独立,即有:
那么联合概率 p ( x ) p(\pmb{x}) p(xxx)可分解为:
是4个局部条件概率的乘积,分别用4个表格来记录4个条件概率,只需1+2+2+4=9个独立参数。
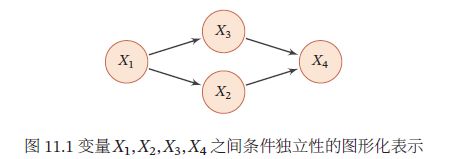
当概率模型中参数多时,其条件依赖关系也复杂,可用图结构方式将模型可视化,简洁描述随机变量之间的条件独立性,并将复杂模型分解为多个简单模型,如图是上述例子的4个变量间的条件独立性的图形化描述,节点表示一个变量,每条边表示变量之间的依赖关系:
图模型的三个基本问题
- 表示问题:对于一个概率模型,如何通过图结构来描述变量之间的依赖关系
- 学习问题:图模型的学习包括图结构、参数的学习,本文只关注给定图结构时的参数学习,即参数估计问题
- 推断问题:已知部分变量,计算其他变量的条件概率分布
图模型与机器学习 很多机器学习模型都可以归纳为概率模型,即建模输入和输出之间的条件概率分布,故,图模型提出了一新角度来解释机器学习模型。这角度优点:了解不同机器学习模型间的联系,方便设计新模型。机器学习中,图模型越来越多被用于设计和分析学习算法。
1. 模型的表示
图由一组节点和节点之间的边组成,在概率模型中,每个节点都表示一随机变量(或一组随机变量),边表示这些随机变量之间的概率依赖问题。
常见的概率图模型分为:有向图模型和无向图模型:
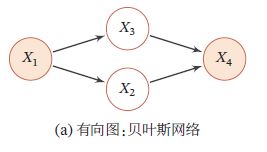
- 有向图模型的图结构为有向非循环图(Directed Acyclic Graph,DAG)。如果两个节点之间有连边,表示对应的两变量为因果关系,即不存在其他变量使得这两个节点对应的变量条件独立
- 无向图模型使用无向图描述变量之间的关系,每条边代表两个变量之间有概率依赖关系,但不一定是因果关系
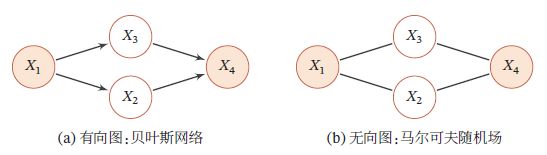
两个示例如下,分别表示四个变量 { X 1 , X 2 , X 3 , X 4 } \{X_1, X_2,X_3,X_4\} { X1,X2,X3,X4}之间的依赖关系,图中带阴影的节点表示可观测到的变量,不带阴影的节点表示隐变量,连边表示两变量间的条件依赖关系:
1.1 有向图模型
有向图模型(Directed Graphical model),也称为贝叶斯网络(Bayesian Network),或信念网络(Belief Network,BN),是一类用有向图来描述随机向量概率分布的模型。

条件独立性 在贝叶斯网络中,如果两个节点直接连接的,他们肯定是非条件独立的,是直接因果关系,父是因,子是果。
如果两个节点不是直接连接,但有一条经过其他节点的路径来连接,那么这两个节点之间的条件独立性比较复杂。以三个节点的贝叶斯网络为例,三个节点 X 1 , X 2 , X 3 X_1, X_2,X_3 X1,X2,X3,其中 X 1 X_1 X1和 X 3 X_3 X3不直接连接,通过节点 X 2 X_2 X2连接,这三个节点之间可以有四种连接关系:
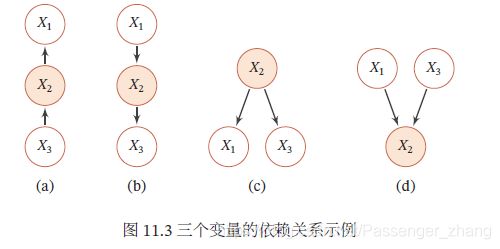
- 间接因果关系(图a):当 X 2 X_2 X2已知时, X 1 X_1 X1和 X 3 X_3 X3为条件独立
- 间接果因关系(图b):当 X 2 X_2 X2已知时, X 1 X_1 X1和 X 3 X_3 X3为条件独立
- 共因关系(图c):当 X 2 X_2 X2未知时, X 1 X_1 X1和 X 3 X_3 X3是不独立的;当 X 2 X_2 X2已知时, X 1 X_1 X1和 X 3 X_3 X3为条件独立
- 共果关系(图d):当 X 2 X_2 X2未知时, X 1 X_1 X1和 X 3 X_3 X3是独立的;当 X 2 X_2 X2已知时, X 1 X_1 X1和 X 3 X_3 X3不独立
局部马尔科夫性质 对一个更一般的贝叶斯网络,其局部马尔科夫性质为:每个随机变量在给定父节点的情况下,条件独立于它的非后代节点,其中 Z Z Z 为 X k X_k Xk的非后代变量:
![]()
1.2 常见的有向图模型
许多经典的机器学习模型如朴素贝叶斯分类器、隐马尔可夫模型、深度信念网络等,可用有向图模型来描述。
1.2.1 Sigmoid信念网络
为减少模型参数,可使用参数化模型来建模有向图中的条件概率分布,一种简单的参数化模型为Sigmoid信念网络。
Sigmoid信念网络(Sigmoid Belief Network,SBN)中的变量取值为{0,1},对于变量 X k X_k Xk和它的父节点集合 π k \pi_k πk,其条件概率分布表示为:
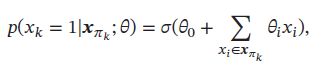
其中 σ ( ⋅ ) \sigma(\cdot) σ(⋅)是Logistc函数, θ i \theta_i θi是可学习的参数,假设变量 X k X_k Xk的父节点数量为 M,如果使用表格来记录条件概率需要 2 M 2^M 2M个参数,如果使用参数化模型只需要M+1个参数。如果对不同的条件概率都共享使用一个参数化模型,其参数数量又可以大幅减少。
Sigmoid信念网络与Logistic回归模型都采用Logistic函数来计算条件概率。如果假设Sigmoid信念网络中只有一个叶子节点,其所有的父节点之间没有连接,且取值为实数,那么Sigmoid信念网络的网络结构和Logistic回归模型类似:
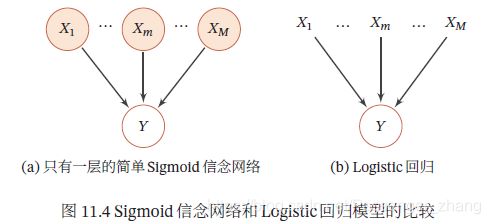
这两个模型区别在于,Logistic回归模型中的 x \pmb{x} xxx作为一种确定性的参数,而非变量,因此,Logistic回归模型只建模条件概率 p ( y ∣ x ) p(y|\pmb{x}) p(y∣xxx),是一种判别模型;Sigmoid信念网络 p ( x , y ) p(\pmb{x},y) p(xxx,y)是一种生成模型。
1.2.2 朴素贝叶斯分类器
朴素贝叶斯分类器(Naive Bayes Classifier,NB)在强(朴素)独立性假设的条件下运用贝叶斯公式来计算每个类别的条件概率。
给定一个有M为特征的样本 x \pmb{x} xxx 和类别 y,类别 y 的条件概率为:
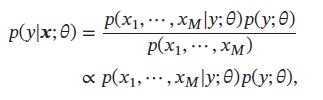
其中 θ \theta θ 为概率分布的参数。
在朴素贝叶斯分类器中,假设在给定 Y 的情况下, X m X_m Xm之间是条件独立的,即 X m ⊥ ⊥ X k ∣ Y , ∀ m ≠ k X_m \perp\!\!\!\!\perp X_k | Y, \forall m \neq k Xm⊥⊥Xk∣Y,∀m=k.朴素贝叶斯分类器的图模型:
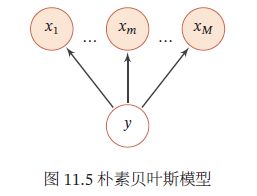
条件概率分布 p ( y ∣ x ) p(y|\pmb{x}) p(y∣xxx)可以分解为:

其中 θ c \theta_c θc是 y 的先验概率分布的参数, θ m \theta_m θm是条件概率分布 p ( x m ∣ y , θ m ) p(x_m|y,\theta_m) p(xm∣y,θm)的参数。若 x m x_m xm为连续值, p ( x m ∣ y ; θ m ) p(x_m|y;\theta_m) p(xm∣y;θm)可以用高斯分布建模;若 x m x_m xm为离散值, p ( x m ∣ y ; θ m ) p(x_m|y;\theta_m) p(xm∣y;θm)可用多项分布建模。
虽然朴素贝叶斯分类器条件独立性假设强,但实际中,朴素贝叶斯分类器在很多任务上效果好,并且模型简单,可有效防止过拟合。
1.2.3 隐马尔科夫模型
隐马尔科夫模型(Hidden Markov Model,HMM)是用来表示一种含有隐变量的马尔科夫过程。下图是隐马尔科夫模型的图模型,其中 X 1 : T X_{1:T} X1:T为可观测变量, Y 1 : T Y_{1:T} Y1:T为隐变量,隐变量构成一个马尔科夫链,每个可观测标量 X t X_t Xt依赖当前时刻的隐变量 Y t Y_t Yt。
隐马尔科夫模型的联合概率可以分解为:
![]()
其中 x \pmb{x} xxx 和 y \pmb{y} yyy分别为可观测变量和隐变量的取值,条件概率 p ( x t ∣ y t , θ t ) p(x_t|y_t,\theta_t) p(xt∣yt,θt)称为输出概率,条件概率 p ( y t ∣ y t − 1 , θ s ) p(y_t|y_{t-1},\theta_s) p(yt∣yt−1,θs)称为转移概率, θ s \theta_s θs和 θ t \theta_t θt分别表示两类条件概率的参数。
1.3 无向图模型
无向图模型也叫马尔科夫随机场(Markov Random Field,MRF)或马尔科夫网络(Markov Network),是一类用无向图来描述一组具有局部马尔科夫性质的随机向量X的联合概率分布模型

无向图的局部马尔科夫性 无向图中的局部马尔科夫性可以表示为:
![]()
其中 X N ( k ) , k \pmb{X}_{\\ N(k),\\ k} XXXN(k),k表示除 X N ( k ) \pmb{X}_{N(k)} XXXN(k) 和 X k X_k Xk外的其他变量.
1.4 无向图模型的概率分解
团 由于无向图模型并不提供一个变量的拓扑排序,无法用链式法则对 p ( x ) p(\pmb{x}) p(xxx)进行逐一分解,无向图模型的联合概率一般以全连通子图为单位进行分解。无向图中的一个全连通子图,称为团(Clique),即团内的所有节点之间都连边。如下图共有7个团: { X 1 , X 2 } , { X 1 , X 3 } , { X 2 , X 3 } , { X 3 , X 4 } , { X 2 , X 4 } , { X 1 , X 2 , X 3 } , { X 2 , X 3 , X 4 } \{X_1, X_2\}, \{X_1, X_3\},\{X_2, X_3\}, \{X_3, X_4\}, \{X_2, X_4\}, \{X_1, X_2, X_3\}, \{X_2, X_3, X_4\} { X1,X2},{ X1,X3},{ X2,X3},{ X3,X4},{ X2,X4},{ X1,X2,X3},{ X2,X3,X4}
所有团中,如果有一个团不能被其他的团包含,这个团就是一个最大团(Maximal Clique)
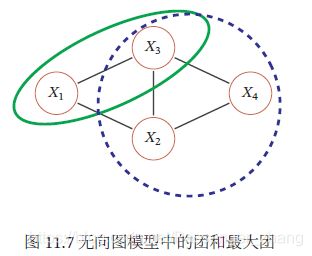
因子分解 无向图中的联合概率可以分解为一系列定义在最大团上的非负函数的乘积形式。

无向图模型和有向图模型的一个重要区别是有配分函数Z。配分函数的计算复杂度是指数级的,因此在推断和参数学习时需要重点考虑。
吉布斯分布 公式(11.16)中定义的分布形式也称为吉布斯分布(Gibbs Distribution)根据定理11.1,无向图模型和吉布斯分布是一致的,吉布斯分布一定满足马尔可夫随机场的条件独立性质,并且马尔可夫随机场的概率分布一定可以表示成吉布斯分布。
由于势能函数必须为正的,因此一般定义为:
![]()
其中 E c ( x c ) E_c(\pmb{x}_c) Ec(xxxc)为能量函数(Energy Function).
因此无向图上定义的概率分布可以表示为:

这种形式的分布又称为玻尔兹曼分布(Boltzmann Distribution)。任何一个无向图模型都可以用上述公式表示其联合概率。
1.5 常见的无向图模型
许多机器学习模型如对数线性模型(最大熵模型)、条件随机场、玻尔兹曼机、受限玻尔兹曼机可用无向图模型描述。
1.5.1 对数线性模型
势能函数一般定义为:
![]()
其中函数 f c ( x c ) f_c(\pmb{x}_c) fc(xxxc)为定义在 x c \pmb{x}_c xxxc上的特征向量, θ c \theta_c θc为权重向量,这样联合概率 p ( x ) p(\pmb{x}) p(xxx)的对数形式为:
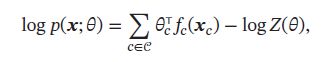
其中 θ \theta θ代表所有势能函数中的参数 θ c \theta_c θc,这种形式的无向图模型又叫对数线性模型、最大熵模型、条件最大熵模型、Softmax回归模型:
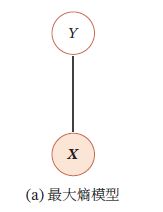
如果使用对数线性模型来建模条件概率 p ( y ∣ x ) p(y|\pmb{x}) p(y∣xxx):
其中 Z ( x ; θ ) = ∑ y e x p ( θ T f y ( x , y ) ) Z(\pmb{x};\theta) = \sum_y exp(\theta^Tf_y(\pmb{x},y)) Z(xxx;θ)=∑yexp(θTfy(xxx,y))
1.5.2 条件随机场
条件随机场(Conditional Random Field,CRF)是一种直接建模条件概率的无向图模型。不同于条件最大熵模型,条件随机场的条件概率 p ( y ∣ x ) p(\pmb{y}|\pmb{x}) p(yyy∣xxx)中, y \pmb{y} yyy一般为随机向量,因此需要对 p ( y ∣ x ) p(\pmb{y}|\pmb{x}) p(yyy∣xxx)进行因子分解。假设条件随机场的最大团集合为 ζ \zeta ζ,其条件概率为:
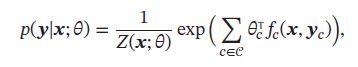
其中 Z ( x ; θ ) = ∑ y e x p ( ∑ c ∈ ζ f c ( x , y c ) T θ c ) Z(\pmb{x};\theta)=\sum_y exp(\sum_{c \in \zeta}f_c(\pmb{x}, \pmb{y}_c)^T\theta_c) Z(xxx;θ)=∑yexp(∑c∈ζfc(xxx,yyyc)Tθc)为归一化项。
一个常用的条件随机场为图所示的链式结构,称为线性链条件随机场(Linear-Chain CRF),其条件概率为:
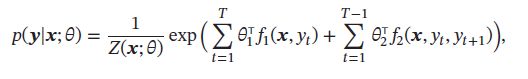
其中 f 1 ( x , y t ) f_1(\pmb{x}, y_t) f1(xxx,yt)为状态特征,一般和位置t相关, f 2 ( x , y t , y t + 1 ) f_2(\pmb{x}, y_t, y_{t+1}) f2(xxx,yt,yt+1)为转移特征,一般可以简化为 f 2 ( y t , y t + 1 ) f_2( y_t, y_{t+1}) f2(yt,yt+1)并使用状态转移矩阵来表示:

1.6 有向图和无向图之间的转换
有向图和无向图可以相互转换,但将无向图转为有向图较困难。在实际应用中,将有向图转为无向图更为重要,这样可以利用无向图上的精确推断算法如联合树算法(Junction Tree Algorithm)。
无向图模型可以表示有向图模型无法表示的依赖关系:循环依赖;但它不能表示有向图模型能够表示的某些关系:因果关系。
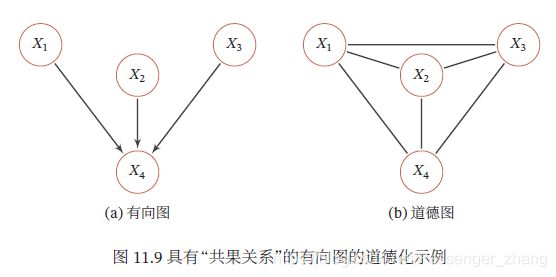
如图下图a,其联合概率分布可以分解为:
![]()
其中 p ( x 4 ∣ x 1 , x 2 , x 3 ) p(x_4|x_1,x_2,x_3) p(x4∣x1,x2,x3)和四个变量都相关,如果转换为无向图,需要将这四个变量都归属于一个团中,因此需要将 x 4 x_4 x4的三个父节点之间加上连边,如图b,这个过程为道德化(Moralization),转换后的无向图称为道德图(Moral Graph)。在道德化的过程中,原来有向图的一些独立性会丢失,比如上例中的 X 1 ⊥ ⊥ X 2 ⊥ ⊥ X 3 ∣ ∅ X_1 \perp\!\!\!\!\perp X_2 \perp\!\!\!\!\perp X_3 | \emptyset X1⊥⊥X2⊥⊥X3∣∅ 在道德图中不再成立:
2. 学习
图模型的学习分两部分:网络结构学习即寻找最优的网络的结构,网络参数估计即已知网络结构,估计每个条件概率分布的参数。
网络结构学习一般困难,常由领域专家来构建。本文只讨论在给定网络结构条件下的参数估计问题,图模型的参数估计问题又分为**(不)包含隐变量时的参数估计问题**
2.1 不含隐变量的参数估计
如果图模型中不包含隐变量,即所有变量都是可观测的,那么网络参数一般可直接通过最大似然来估计。
有向图模型 在有向图模型中,所有变量 x \pmb{x} xxx的联合概率分布可以分解为每个随机变量 x k x_k xk 的局部条件概率 p ( x k ∣ x π k ; θ k ) p(x_k|x_{\pi_k};\theta_k) p(xk∣xπk;θk) 的连乘形式,其中 θ k \theta_k θk为第k个变量的局部条件概率的参数。
给定N个训练样本,其对数似然函数为:
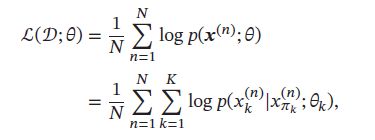
其中 θ k \theta_k θk 为模型中的所有参数。
因为所有变量都是可观测的,最大化对数似然 L ( D ; θ ) L(D;\theta) L(D;θ),只需要分别地最大化每个变量的条件似然来估计其参数。
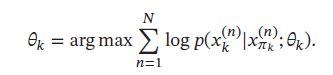
如果变量 x \pmb{x} xxx是离散的,直接简单的方式是在训练集上统计每个变量的条件概率表,但需要的参数多:假设条件概率 p ( x k ∣ x π k ) p(x_k|x_{\pi_k}) p(xk∣xπk)的父节点数量为M,所有变量为二值变量,其条件概率表需要 2 M 2^M 2M个参数。故可使用参数化的模型如Sigmoid信念网络。如果变量 x \pmb{x} xxx连续,可使用高斯函数来表示条件概率分布,称为高斯信念网络。在此基础上,可通过让所有的条件概率分布共享使用同一组参数来进一步减少参数。
无向图模型 所有变量 x \pmb{x} xxx的联合概率分布可以分解为定义在最大团上的势能函数的连乘形式,一对数线性模型为例:

其中 Z ( θ ) = ∑ x e x p ( ∑ c ∈ ζ θ c T f c ( x c ) ) Z(\theta)=\sum_x exp(\sum_{c \in \zeta}\theta_c^T f_c(\pmb{x}_c)) Z(θ)=∑xexp(∑c∈ζθcTfc(xxxc)).
给定N个训练样本,其对数似然函数为:
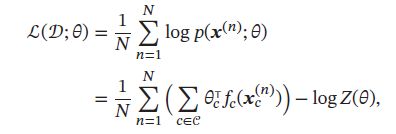
其中 θ c \theta_c θc为定义在团c上的势能函数的参数。
采用梯度上升方法进行最大似然估计, L ( D ; θ ) L(D;\theta) L(D;θ)关于参数 θ c \theta_c θc的偏导数为:

其中
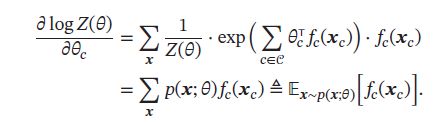
故

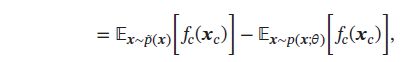
其中 p ^ ( x ) \hat{p}(\pmb{x}) p^(xxx) 定义为经验分布(Empirical Distribution)。由于在最优点时梯度为0,故无向图的最大似然估计的优化目标等价于:对于每个团c上的特征 f c ( x c ) f_c(\pmb{x}_c) fc(xxxc),使得其在经验分布 p ^ ( x ) \hat{p}(\pmb{x}) p^(xxx) 下的期望等于其在模型分布 p ( x ; θ ) p(\pmb{x};\theta) p(xxx;θ) 下的期望
对比公式

和

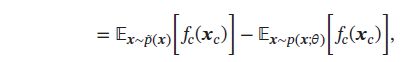
可以看出,无向图模型的参数估计要比有向图更为复杂,在有向图中,每个局部条件概率的参数是独立的;无向图中,所有的参数是相关的,无法分解。
对于一般的无向图模型,公式:
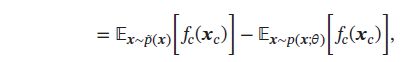
中的第一个减项很难计算,因为涉及在联合概率空间 p ( x ; θ ) p(\pmb{x};\theta) p(xxx;θ)计算期望,当模型变量比较多时,这个计算往往无法实现,故,无向图的参数估计通常采用近似的方法:一是利用采样来近似计算期望;二是用坐标上升法即固定其他参数,来优化一个势能函数的参数。
2.2 含隐变量的参数估计
图模型中包含隐变量,即部分变量不可测,就需要EM算法来进行参数估计
2.2.1 EM算法
在一个包含隐变量的图模型中,令 X 定义为可观测变量集合,令 Z 定义为隐变量集合,一个样本 x 的边际似然函数(Marginal Likelihood)为

其中 θ \theta θ 为模型参数,边际似然函数称为证据(Evidence)。
下图给出了带隐变量的贝叶斯网络的图模型结构,其中矩形表示其中的变量重复N次,这种表示方法称为 盘子表示法(Plate Notation),是图模型中表示重复变量的方法。

给定N个训练样本,整个训练集的对数边际似然为:
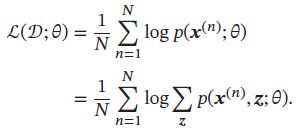
通过最大化整个训练集的对数边际似然,可以估计出最优的参数 θ ∗ \theta^* θ∗,然而计算边际似然函数时涉及 p ( x ) p(\pmb{x}) p(xxx)的推断问题,需要在对数函数的内部进行求和(或积分)。这样,当计算参数 θ \theta θ的梯度时,这个求和操作依然存在,除非 p ( x , z ; θ ) p(\pmb{x,z};\theta) p(x,zx,zx,z;θ)的形式非常简单,否则这个求和难以直接计算。
为了计算 log p ( x ; θ ) \log p(\pmb{x};\theta) logp(xxx;θ),我们引入一个额外的变分函数 q ( z ) q(z) q(z), q ( z ) q(z) q(z)定义为在隐变量Z上的分布,样本x的对数边际似然函数为:
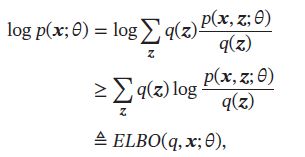
其中 E L B O ( q , x ; θ ) ELBO(q,\pmb{x};\theta) ELBO(q,xxx;θ)为对数边际似然函数 l o g p ( x ; θ ) log p(\pmb{x};\theta) logp(xxx;θ)的下界,称为证据下界(Evidence Lower BOund,ELBO).
上述公式使用了 Jensen不等式,即对于凹函数g, E [ g ( X ) ] ≤ g ( E [ X ] ) E[g(X)] \leq g(E[X]) E[g(X)]≤g(E[X])成立,由Jensen不等式的性质可知,仅当 q ( z ) = p ( z ∣ x ; θ ) q(z)=p(z|x;\theta) q(z)=p(z∣x;θ)时, log p ( x ; θ ) = E L B O ( q , x ; θ ) \log p(\pmb{x};\theta) = ELBO(q,\pmb{x};\theta) logp(xxx;θ)=ELBO(q,xxx;θ)
这样,最大化对数边际似然函数 log p ( x ; θ ) \log p(\pmb{x};\theta) logp(xxx;θ)的过程可以分解为两个步骤:
- 先找到近似分布 q ( z ) q(\pmb{z}) q(zzz)使得 log p ( x ; θ ) = E L B O ( q , x ; θ ) \log p(\pmb{x};\theta) = ELBO(q,\pmb{x};\theta) logp(xxx;θ)=ELBO(q,xxx;θ)
- 再寻找参数 θ \theta θ最大化 E L B O ( q , x ; θ ) ELBO(q,\pmb{x};\theta) ELBO(q,xxx;θ)。这就是期望最大化(Expectation Maximum,EM)算法
EM算法是隐含变量图模型的常用参数估计算法,通过迭代的方法来最大化边际似然,EM算法具体分为两个步骤:E步和M步。不断重复这两步,直到收敛到某个局部最优解,在第 t 步更新时,E步 和 M步分别为:
- E步(Expectation Step):固定参数 θ t \theta_t θt,找到一个分部 q t + 1 ( z ) q_{t+1}(z) qt+1(z)使得证据下界 E L B O ( q , x ; θ t ) = log p ( x ; θ t ) ELBO(q,\pmb{x};\theta_t) = \log p(\pmb{x};\theta_t) ELBO(q,xxx;θt)=logp(xxx;θt).根据Jensen不等式, q ( z ) = p ( z ∣ x , θ t ) q(\pmb{z})=p(\pmb{z}|\pmb{x},\theta_t) q(zzz)=p(zzz∣xxx,θt)时, E L B O ( q , x ; θ t ) ELBO(q,\pmb{x};\theta_t) ELBO(q,xxx;θt)最大。故,在E步中,最理想的分布 q ( z ) q(\pmb{z}) q(zzz)等于后验分布 p ( z ∣ x , θ t ) p(\pmb{z}|\pmb{x},\theta_t) p(zzz∣xxx,θt),而计算后验分布 p ( z ∣ x , θ t ) p(\pmb{z}|\pmb{x},\theta_t) p(zzz∣xxx,θt)是一个推断(Inference)问题,如果z是有限的一维离散变量(如高斯混合模型), p ( z ∣ x ; θ t ) p(z|x;\theta_t) p(z∣x;θt)计算起来比较容易;否则, p ( z ∣ x ; θ t ) p(z|x;\theta_t) p(z∣x;θt)很难计算,需要通过变分推断的方法进行近似估计。
- M步(Maximization Step):固定 q t + 1 ( z ) q_{t+1}(z) qt+1(z),找到一组参数使得证据下界最大,

这一步可以看做是全观测变量图模型的参数估计问题, 使用2.1节中方法进行参数估计。
收敛性证明 假设在第 t 步时的模型参数为 θ t \theta_t θt,在 E步 时找到一个分布 q t + 1 ( z ) q_{t+1}(\pmb{z}) qt+1(zzz)使得 log p ( x ∣ θ t ) = E L B O ( q t + 1 , x ; θ t ) \log p(\pmb{x}|\theta_t)=ELBO(q_{t+1},\pmb{x};\theta_t) logp(xxx∣θt)=ELBO(qt+1,xxx;θt)。在M步时固定 q t + 1 ( z ) q_{t+1}(\pmb{z}) qt+1(zzz) 找到一组参数 θ t + 1 \theta_{t+1} θt+1,使得 E L B O ( q t + 1 , x ∣ θ t ) ≤ E L B O ( q t + 1 , x ∣ θ t + 1 ) ELBO(q_{t+1},\pmb{x}|\theta_t)\leq ELBO(q_{t+1},\pmb{x}|\theta_{t+1}) ELBO(qt+1,xxx∣θt)≤ELBO(qt+1,xxx∣θt+1),因此有:
![]()
即每经过一次迭代,对数边际似然增加,即 log p ( x ; θ t ) ≤ log p ( x ; θ t + 1 ) \log p(\pmb{x};\theta_{t}) \leq \log p(\pmb{x};\theta_{t+1}) logp(xxx;θt)≤logp(xxx;θt+1)
信息论的视角 对数边际似然 log p ( x ; θ ) \log p(\pmb{x};\theta) logp(xxx;θ)可以通过下面方式进行分解:
首先因为 p ( x , z ; θ ) = p ( z ∣ x ; θ ) + p ( x ; θ ) p(\pmb{x},\pmb{z};\theta)=p(\pmb{z}|\pmb{x};\theta) + p(\pmb{x};\theta) p(xxx,zzz;θ)=p(zzz∣xxx;θ)+p(xxx;θ),进一步有: p ( x ; θ ) = p ( x , z ; θ ) − p ( z ∣ x ; θ ) p(\pmb{x};\theta) = p(\pmb{x},\pmb{z};\theta) - p(\pmb{z}|\pmb{x};\theta) p(xxx;θ)=p(xxx,zzz;θ)−p(zzz∣xxx;θ)
这样边际似然函数 p ( x ; θ ) p(\pmb{x};\theta) p(xxx;θ)可以分解为:
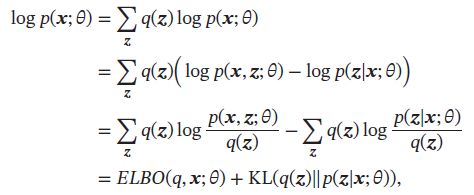
其中 K L ( q ( z ) ∣ ∣ p ( z ∣ x ; θ ) ) KL(q(\pmb{z})||p(\pmb{z}|\pmb{x};\theta)) KL(q(zzz)∣∣p(zzz∣xxx;θ))为分布 q ( z ) q(\pmb{z}) q(zzz)和后验分布 p ( z ∣ x ; θ ) ) p(\pmb{z}|\pmb{x};\theta)) p(zzz∣xxx;θ))的KL散度。
由于 0 ≤ K L ( q ( z ) ∣ ∣ p ( z ∣ x ; θ ) ) 0 \leq KL(q(\pmb{z})||p(\pmb{z}|\pmb{x};\theta)) 0≤KL(q(zzz)∣∣p(zzz∣xxx;θ)),因此 E L B O ( q , x ; θ ) ELBO(q,\pmb{x};\theta) ELBO(q,xxx;θ)为 log p ( x ; θ ) \log p(\pmb{x};\theta) logp(xxx;θ)的一个下界。当且仅当 q ( z ) = p ( z ∣ x ; θ ) ) q(\pmb{z})=p(\pmb{z}|\pmb{x};\theta)) q(zzz)=p(zzz∣xxx;θ))时, K L ( q ( z ) ∣ ∣ p ( z ∣ x ; θ ) ) = 0 KL(q(\pmb{z})||p(\pmb{z}|\pmb{x};\theta))=0 KL(q(zzz)∣∣p(zzz∣xxx;θ))=0 这时 E L B O ( q , x ; θ ) = log p ( x ; θ ) ELBO(q,\pmb{x};\theta)=\log p(\pmb{x};\theta) ELBO(q,xxx;θ)=logp(xxx;θ)
2.2.2 高斯混合模型
EM算法的应用例子:高斯混合模型。高斯混合模型(Gaussian Mixture Model,GMM)由多个高斯分布组成的模型,其总体密度函数为多个高斯密度函数的加权组合。如果一个连续随机变量或连续随机向量的分布比较复杂,那么我们通常可以用高斯混合模型来估计其分布情况。
不失一般性,考虑一维的情况,假设样本 x \pmb{x} xxx 是从K个高斯分布中的一个分布生成的,但是无法观测到具体是由哪个分布生成。我们引入一个隐变量 z ∈ { 1 , ⋯ , K } z \in \{1,\cdots,K\} z∈{ 1,⋯,K} 来表示样本 x 来自哪个高斯分布,z 服从多项分布:
![]()
其中 π = [ π 1 , ⋯ , π K ] \pi =[\pi_1,\cdots,\pi_K] π=[π1,⋯,πK]为多项分布的参数,并满足 0 ≤ π k ∀ k , ∑ k = 1 K π k = 1 0 \leq \pi_k \forall k,\sum_{k=1}^K \pi_k=1 0≤πk∀k,∑k=1Kπk=1。 π k \pi_k πk表示样本x由第k个高斯分布生成的概率。
给定 z = k z=k z=k,条件分布 p ( x ∣ z = k ) p(x|z=k) p(x∣z=k)为高斯分布:
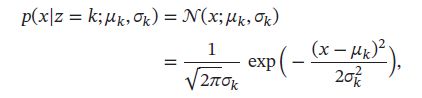
其中 μ k \mu_k μk 和 σ k \sigma_k σk分别为第k个高斯分布的均值和方差。
从高斯混合模型中生成一个样本 x 的过程可以分为两步:
- 首先根据多现实分布 p ( z ∣ π ) p(z|\pi) p(z∣π)随机选取一个高斯分布
- 假设选中第k个高斯分布(即z=k),再从高斯分布 N ( x ; μ k , σ k ) N(x;\mu_k,\sigma_k) N(x;μk,σk)中选取一个样本x
参数估计 给定N个有高斯混合模型生成的训练样本 x ( 1 ) , x ( 2 ) , ⋯ , x ( N ) x^{(1)},x^{(2)},\cdots,x^{(N)} x(1),x(2),⋯,x(N),希望能学习其中的参数 π k , μ k , σ k , 1 ≤ k ≤ K \pi_k, \mu_k, \sigma_k, 1 \leq k \leq K πk,μk,σk,1≤k≤K。由于我们无法观测样本 x ( n ) x^{(n)} x(n)是从哪个高斯分布生成的,故无法直接用最大似然来进行估计。
对每个样本 x ( n ) x^{(n)} x(n),其对数边际分布为
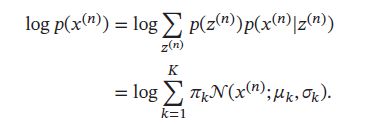
根据EM算法,参数估计可以分为两步进行迭代:
E步 先固定参数 μ , σ \mu, \sigma μ,σ,计算后验分布 p ( z ( n ) ∣ x ( n ) ) p(z^{(n)}|x^{(n)}) p(z(n)∣x(n))
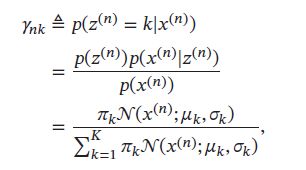
其中 γ n k \gamma_{nk} γnk定义了样本 x ( n ) x^{(n)} x(n) 属于第 k 个高斯分布的后验概率。
M步 令 q ( z = k ) = γ n k q(z=k)=\gamma_{nk} q(z=k)=γnk,训练集D的证据下界为:
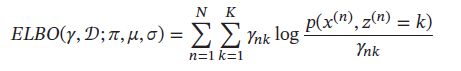
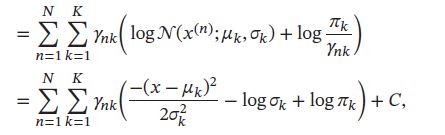
其中 C为何参数无关的常数。
将参数估计问题转化为优化问题:
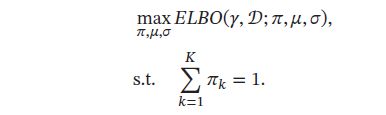
利用拉格朗日方法,分别求拉格朗日函数 E L B O ( γ , D ; π , μ , σ ) + λ ( ∑ k = 1 K π k − 1 ) ELBO(\gamma,D;\pi,\mu,\sigma) + \lambda(\sum_{k=1}^K \pi_k -1) ELBO(γ,D;π,μ,σ)+λ(∑k=1Kπk−1)关于 π , μ , σ \pi,\mu,\sigma π,μ,σ的偏导数,并令其等于0,可得:

其中:

高斯混合模型的参数学习过程如下:

下图是一个高斯混合模型训练过程的简单示例,给定一组数据,我们用两个高斯分布来估计这组数据的分布情况:

3. 推断
图模型中,推断(Inference)是指在观测到变量部分 e = { e 1 , e 2 , ⋯ , e M } \pmb{e}=\{e_1,e_2,\cdots,e_M\} eee={ e1,e2,⋯,eM} 时,计算其他变量的某个子集 q = { q 1 , q 2 , ⋯ , q N } \pmb{q}=\{q_1,q_2,\cdots,q_N\} qqq={ q1,q2,⋯,qN}的条件概率 p ( q ∣ e ) p(\pmb{q}|\pmb{e}) p(qqq∣eee)
假设一个图模型中,除了变量 e \pmb{e} eee、 q \pmb{q} qqq外,其余变量表示为 z \pmb{z} zzz,根据贝叶斯公式有:

因此,图模型的推断问题的关键为求任意一个变量子集的边际概率分布问题。
在图模型中,常用的推断算法可以分为精确推断算法和近似推断算法。
3.1 精确推断
精确推断(Exact Inference)算法是指可以计算出条件概率 p ( q ∣ e ) p(\pmb{q}|\pmb{e}) p(qqq∣eee) 的精确解的算法
3.1.1 变量消除法
以图a 额有向图为例,假设推断问题为计算后验概率 p ( x 1 ∣ x 4 ) p(x_1|x_4) p(x1∣x4),需要计算两个边际概率 p ( x 1 , x 4 ) p(x_1,x_4) p(x1,x4) 和 p ( x 4 ) p(x_4) p(x4)。
假设每个变量取 K 个值,计算上面的边际分布需要 K 2 K^2 K2 次加法以及 K 2 × 3 K^2 \times 3 K2×3次乘法。
根据乘法分配率:
a b + a c = a ( b + c ) ab+ac=a(b+c) ab+ac=a(b+c)
边际概率 p ( x 1 , x 4 ) p(x_1,x_4) p(x1,x4)可以写为:
这样计算量可以减少到 K 2 + K K^2+K K2+K次加法和 K 2 + K + 1 K^2+K+1 K2+K+1次乘法
这种方法是利用动态规划的思想,每次消除一个变量,来减少计算边际分布的计算复杂度,称为变量消除法(Variable Elimination Algorithm)。随着图模型规模的增长,变量消除法的收益越大。
变量消除法可以按照不同的顺序来消除变量,比如上面的推断问题也可以按照 x 2 , x 3 x_2,x_3 x2,x3的消除顺序来进行计算
同理,边际概率 p ( x 4 ) p(x_4) p(x4) 可以通过以下方式来计算:

变量消除法的一个缺点是在计算多个边际分布时存在很多重复的计算,比如上面的图模型中,计算边际概率 p ( x 4 ) p(x_4) p(x4)和 p ( x 3 ) p(x_3) p(x3)时很多局部的求和计算是一样的。
3.1.2 信念传播算法
信念传播(Belief Propagation,BP)算法,也称为和积(Sum-Product)算法或信息传递(Message Passing)算法,是将变量消除法中的和积操作看做消息(Message),并保存起来,这样可以节省大量的计算资源。
链式结构上的信念传播算法

以上图为例,其联合概率 p ( x ) p(\pmb{x}) p(xxx)为:
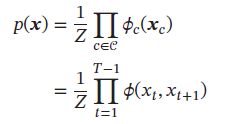
其中 ϕ ( x t , x t + 1 ) \phi(x_t,x_{t+1}) ϕ(xt,xt+1)是定义在团 ( x t , x t + 1 ) (x_t,x_{t+1}) (xt,xt+1)的势能函数。
第 t 个变量的边际概率 p ( x t ) p(x_t) p(xt)为:
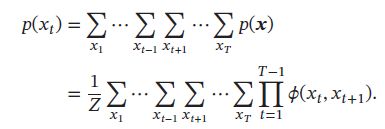
假设每个变量取K个值,不考虑归一化项,通过上述公式计算边际分布需要 K T − 1 K^{T-1} KT−1次加法以及 K T − 1 × ( T − 1 ) K^{T-1} \times (T-1) KT−1×(T−1)次乘法
根据乘法的分配率,边际概率 p ( x t ) p(x_t) p(xt)可以通过下面方式进行计算:
μ t − 1 , t ( x t ) \mu_{t-1,t}(x_t) μt−1,t(xt) 定义为变量 X t − 1 X_{t-1} Xt−1向变量 X t X_t Xt传递的消息,定义为:
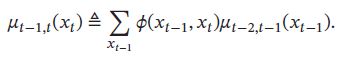
μ t + 1 , t ( x t ) \mu_{t+1,t}(x_t) μt+1,t(xt) 是变量 X t + 1 X_{t+1} Xt+1向变量 X t X_t Xt传递的消息,定义为:
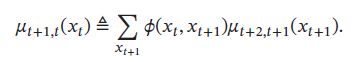
μ t − 1 , t ( x t ) \mu_{t-1,t}(x_t) μt−1,t(xt) 和 μ t + 1 , t ( x t ) \mu_{t+1,t}(x_t) μt+1,t(xt)都可以递归计算,因此,边际概率 p ( x t ) p(x_t) p(xt)的计算复杂度减少为 O ( T K 2 ) O(TK^2) O(TK2),如果要计算整个序列上的所有变量的边际概率,不需要将消息传递的过程重复T次,因为其中每两个相邻节点上的消息是相同的。
链式结构图模型的消息传递过程为:
- 依次计算前向传递的消息 μ t − 1 , t ( x t ) , t = 1 , ⋯ , T − 1 \mu_{t-1,t}(x_t), t=1,\cdots,T-1 μt−1,t(xt),t=1,⋯,T−1
- 依次计算反向传播的消息 μ t + 1 , t ( x t ) , t = T − 1 , ⋯ , 1 \mu_{t+1,t}(x_t), t=T-1,\cdots,1 μt+1,t(xt),t=T−1,⋯,1
- 在任意节点 t 上计算佩芬函数Z:
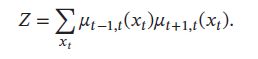
这样就可以通过公式(11.77)计算所有变量的边际概率
树结构上的信念传播算法 信念传播算法也可以推广到具有树结构的图模型上。如果有一个有向图满足任意两个变量只有一条路径,且只有一个没有父节点的节点,那么这个有向图为树结构,其中唯一没有父节点的节点称为根节点。如果一个无向图满足任意两个变量只有一条路径,那么这个无向图也为树结构,在树结构的无向图中,任意一个节点都可以作为根节点。
树结构图模型的消息传递过程为:
- 从叶子节点到根节点依次计算并传递消息
- 从根节点开始到叶子节点,依次计算并传递消息
- 在每个节点上计算所有接受消息的乘积(若是无向图,还需归一化),就得到了所有变量的边际概率
如果图结构中存在环路,可以使用联合树算法(Junction Tree Algorithm)来将图结构转换为无环图。
3.2 近似推断
实际中,精确推断一般用于结构简单的推断问题,当图模型复杂时,精确推断计算开销大,此外,若图模型中的变量时连续的,并且其节分函数没有闭行(Closed-Form)解,也无法使用精确推断。
近似推断(Approximate Inference)主要有三种方法:
- 环路信念传播:当图模型中存在环路,使用信念传播算法时,消息会在环路中一直传递,可收敛或不收敛。环路信念传播(Loopy Belief Propagation,LBP)是在具有环路的图上依然使用信念传播算法,即使得到不精确解,在某些任务上也可以近似精确解。
- 变分推断:图模型中有些变量的局部条件分布可能非常复杂,或其积分无法计算,变分推断(Variational Inference)是引入一个变分分布(常是简单的)来近似条件概率,然后通过迭代的方法来进行计算,首先是更新变分分布的参数来最小化变分分布和真实分布的差异(如交叉熵或KL距离),然后根据变分分布来进行推断
- 采样法:采样法(Sampling Method)通过模拟的方式来采集符合某个分布 p ( x ) p(\pmb{x}) p(xxx)的一些样本,并通过这些样本来估计和这个分布有关的运算,如期望。
4. 近似推断-变分推断
变分法(Calculus Of Variations)主要研究变分问题,即泛函的极值问题。
函数(Function)是表示自变量到因变量的映射关系: y = f ( x ) y=f(x) y=f(x)。而泛函(Functional)是函数的函数,即输入是函数,输出是实数: F ( f ( x ) ) F(f(x)) F(f(x)),一般称 F ( f ( x ) ) F(f(x)) F(f(x))为 f ( x ) f(x) f(x)满足一定的边界条件,并且具有连续的二阶导数。一个泛函的例子是熵,其输入是一个概率分布 p ( x ) p(x) p(x),输出是该分布的不确定性。
微积分可用来寻找函数 f ( x ) f(x) f(x)的极值点,变分布可用来寻找一个函数 f ( x ) f(x) f(x)使得泛函 F ( f ( x ) ) F(f(x)) F(f(x))取得极大或极小值,变方法的应用广泛,如最大熵问题,即寻找一个概率分布,使得该概率分布的熵最大。
贝叶斯模型中, x \pmb{x} xxx为观测变量, z \pmb{z} zzz为隐变量(参数可看做随机变量,包含在 z \pmb{z} zzz中),推断问题为计算条件概率 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx),根据贝叶斯公式,条件概率可写为:
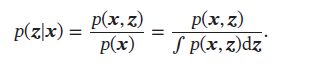
对于很多模型,计算上述公式的积分不可行,因为积分没有闭式解,或计算复杂度是指数级的。
变分推断(Variational Inference)是变分法在推断问题中的应用,寻找一个简单分布 q ∗ ( z ) q^*(\pmb{z}) q∗(zzz)来近似条件概率密度 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx),也称为变分贝叶斯(Variational Bayesian)这样,推断问题转换为一个泛函优化问题:

其中 Q Q Q为候选的概率分布族,由于 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx)难计算,因此不能直接优化上面公式的KL散度。
在EM算法中已证明:
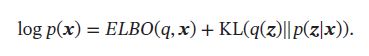
在EM算法的E步中,我们假设 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx)是可计算的,并让 q ( z ) = p ( z ∣ x ) q(\pmb{z})=p(\pmb{z}|\pmb{x}) q(zzz)=p(zzz∣xxx),这样 E L B O ( q , x ) = log p ( x ) ELBO(q,\pmb{x})=\log p(\pmb{x}) ELBO(q,xxx)=logp(xxx)而变分推断可看做是EM算法拓展版,主要处理不能精确推断 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx)的情况。
根据上述两你是有:
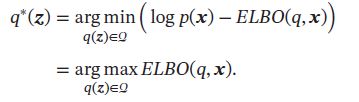
这样公式中优化问题转换为寻找一个简单分布 q ∗ ( z ) q^*(\pmb{z}) q∗(zzz)来最大化证据下界 E L B O ( q , x ) ELBO(q,\pmb{x}) ELBO(q,xxx)
在变分推断中,候选分布族Q的复杂性决定了优化问题的复杂性。一个通常的选择是平均场分布族,即 z \pmb{z} zzz可以分拆为多组相互独立的变量,概率密度可以分解为:
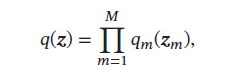
其中 z m \pmb{z}_m zzzm是隐变量的子集,可以是单变量,也可以是一组多元变量。
证据下界可以写为:
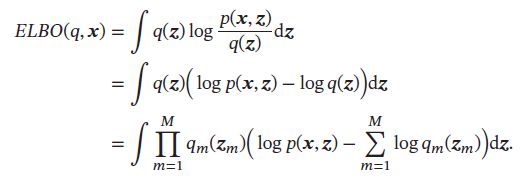
假设只关心隐变量的子集 z j \pmb{z}_j zzzj的近似分布 q j ( z j ) q_j(\pmb{z}_j) qj(zzzj),上式可以写为:
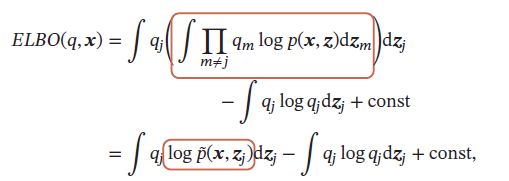
其中 p ^ ( x , z j ) \hat{p}(\pmb{x},\pmb{z}_j) p^(xxx,zzzj)可以看作是一个关于 z j \pmb{z}_j zzzj的未归一化的分布,有:
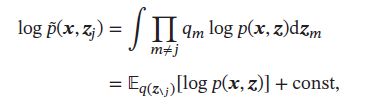
其中 z j \pmb{z}_{\\ j} zzzj为除变量子集 z j \pmb{z}_{j} zzzj外的其他隐变量。
假设固定 z j \pmb{z}_{j} zzzj不变,先优化 q j ( z j ) q_j(\pmb{z}_j) qj(zzzj)使得 E L B O ( q , x ) ELBO(q,\pmb{x}) ELBO(q,xxx)最大。 E L B O ( q , x ) ELBO(q,\pmb{x}) ELBO(q,xxx)可以看做是 − K L ( z j ∣ ∣ p ^ ( x , z j ) ) -KL(\pmb{z}_{j}||\hat{p}( \pmb{x},\pmb{z}_j)) −KL(zzzj∣∣p^(xxx,zzzj))加上一个常数。因此,最小化KL散度 K L ( z j ∣ ∣ p ^ ( x , z j ) ) KL(\pmb{z}_{j}||\hat{p}( \pmb{x},\pmb{z}_j)) KL(zzzj∣∣p^(xxx,zzzj))等于最大化公式:

即最优的 q j ∗ ( z j ) q_j^*(\pmb{z}_j) qj∗(zzzj)正比于对数联合概率密度 log p ( x , z ) \log p(\pmb{x},\pmb{z}) logp(xxx,zzz)的期望的指数:

其中期望根据 q ( z j ) q(\pmb{z_{\\j}}) q(zjzjzj)计算的,我们可以通过选择合适的 q m ( z m ) , 1 ≤ m ≤ M q_m(z_m),1\leq m \leq M qm(zm),1≤m≤M使得这个期望有闭式解。
由于 q j ∗ ( z j ) q_j^*(\pmb{z}_j) qj∗(zzzj)的计算要依赖于其他隐变量,可用坐标上升法来迭代优化每个 q j ∗ ( z j ) , j = 1 , ⋯ , M q_j^*(\pmb{z}_j) ,j=1,\cdots,M qj∗(zzzj),j=1,⋯,M通过不断迭代运用上述公式,证据下界 E L B O ( q , x ) ELBO(q,\pmb{x}) ELBO(q,xxx)会收敛到一个局部最优解。
变分推断通常和参数学习一起使用,比如在EM 算法的E 步中来近似条件分布 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx)
在变分推断中,选择一些简单的分布 q ( z ) q(\pmb{z}) q(zzz)来近似推断 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx).当 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx)比较复杂时,近似效果不佳。这时可以利用神经网络来近似 p ( z ∣ x ) p(\pmb{z}|\pmb{x}) p(zzz∣xxx),这种思想被应用在变分自编码器中.
5. 基于采样法的近似推断
在很多实际任务中,推断出概率分布不是目的,目的是基于这个概率分布进行进一步计算并作出决策。通常这些计算和期望有关。
不是一般性,假设要推断的概率分布为 p ( x ) p(x) p(x),并基于 p ( x ) p(x) p(x)来计算函数 f ( x ) f(x) f(x)的期望:

当 p ( x ) p(x) p(x)比较复杂或难以精确推断时,可通过采样法来近似计算期望 E p [ f ( x ) ] E_p[f(x)] Ep[f(x)]的解
5.1 采样法
采样法(Sampling Method)也称为蒙特卡罗方法(Monte Carlo Method)或统计模拟方法。是一种通过随机采样来近似估计一些计算问题数值解的方法。随机采样指从给定概率密度 p ( x ) p(x) p(x)中抽取出符合其概率分布的样本。
为计算下述公式:
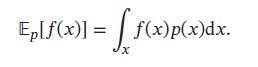
可以通过数值解的方法来近似计算。首先从 p ( x ) p(x) p(x)中独立抽取N个样本 x ( 1 ) , ⋯ , x ( N ) x^{(1)},\cdots,x^{(N)} x(1),⋯,x(N), f ( x ) f(x) f(x)的期望可以用这N个样本的均值 f ^ N \hat{f}_N f^N来近似,即:
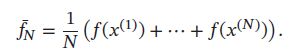
根据大数定律,N趋于无穷时,样本均值收敛于期望值,这就是采样法的理论依据:
![]()
采样法的一个简单应用就是计算圆周率 π \pi π
随机采样 采样法的难点是如何进行随机采样,即如何让计算机生成满足概率密度函数 p ( x ) p(x) p(x)的样本。计算机比较容易生成 [ 0 , 1 ] [0,1] [0,1]区间上均匀分布的样本,如果要生成非均匀分布的样本,要一个间接采样方法。
如果一个分布的概率密度函数为 p ( x ) p(x) p(x),其累计分布函数 c d f − 1 ( y ) , y ∈ [ 0 , 1 ] cdf^{-1}(y),y \in [0,1] cdf−1(y),y∈[0,1],那么可利用累计分布函数的逆函数来生成服从该随机分布的样本。假设 ξ \xi ξ是 [ 0 , 1 ] [0,1] [0,1]区间上均匀分布的随机变量,则 c d f − 1 ( ξ ) cdf^{-1}(\xi) cdf−1(ξ)服从概率密度函数为 p ( x ) p(x) p(x)的分布。
如果一个分布的概率密度函数为 p ( x ) p(x) p(x),其累计分布函数 c d f − 1 ( y ) , y ∈ [ 0 , 1 ] cdf^{-1}(y),y \in [0,1] cdf−1(y),y∈[0,1],那么可利用累计分布函数的逆函数来生成服从该随机分布的样本。假设 ξ \xi ξ是 [ 0 , 1 ] [0,1] [0,1]区间上均匀分布的随机变量,则 c d f − 1 ( ξ ) cdf^{-1}(\xi) cdf−1(ξ)服从概率密度函数为 p ( x ) p(x) p(x)的分布。
但当 p ( x ) p(x) p(x)非常复杂,其累积分布函数的逆函数难以计算,或者不知道 p ( x ) p(x) p(x)的精确值,只知道未归一化的分布 p ^ ( x ) \hat{p}(x) p^(x),则难以直接对 p ( x ) p(x) p(x)进行采样,往往需要使用一些间接的采样策略,如拒绝采样、重要性采样、马尔科夫链蒙特卡罗采样等,这些方法一般根据一个比较容易采样的分布进行采样,然后通过一些策略来间接得到符合 p ( x ) p(x) p(x)分布的样本。
5.2 拒绝采样
拒绝采样(Rejection Sampling)是一种间接采样方法,也称为接受-拒绝采样(Acceptance-Rejection Sampling).
假设原始分布 p ( x ) p(x) p(x)难以直接采样,可引入一个容易采样的分布 q ( x ) q(x) q(x),一般称为提议分布(Proposal Distribution),然后以某个标准拒绝一部分的样本使得最终采样的样本服从分布 p ( x ) p(x) p(x)
拒绝采样中,已知未归一化的分布 p ^ ( x ) \hat{p}(x) p^(x),需构建一个提议分布 q ( x ) q(x) q(x)和一个常数k,使得 k q ( x ) kq(x) kq(x)可以覆盖函数 p ^ ( x ) \hat{p}(x) p^(x),即 p ^ ( x ) ≤ k q ( x ) , ∀ x \hat{p}(x) \leq kq(x),\forall x p^(x)≤kq(x),∀x:

对于每次抽取的样本 x ^ \hat{x} x^,计算接受概率(Acceptance Probability):
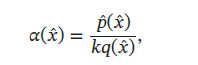
并以概率 α ( x ^ ) \alpha(\hat{x}) α(x^)来接受样本 x ^ \hat{x} x^。拒绝采样的采样过程如下:

判断一个拒绝采样方法的好坏就是看其采样效率,即总体的接受率。如果函数 k q ( x ) kq(x) kq(x)远大于原始分布函数 p ^ ( x ) \hat{p}(x) p^(x),拒绝率会比较高,采样效率不理想. 但要找到一个和 p ^ ( x ) \hat{p}(x) p^(x)比较接近的提议分布往往比较困难,特别是在高维空间中,其采样率非常低,很难应用到实际中.
5.3 重要性采样
如果采样的目的是计算分布 p ( x ) p(x) p(x)下函数 f ( x ) f(x) f(x)的期望,那么实际上抽取的样本不需要严格服从分布 p ( x ) p(x) p(x),也可通过另一个分布,即提议分布 q ( x ) q(x) q(x),直接采样并估计 E p [ f ( x ) ] E_p[f(x)] Ep[f(x)],其中 w ( x ) w(x) w(x)称为重要性权重:
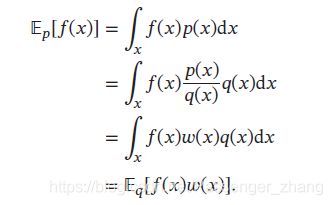
重要性采样(Importance Sampling)是通过引入重要性权重,将分布 p ( x ) p(x) p(x)下 f ( x ) f(x) f(x)的期望变为在分布q(x)下 f ( x ) w ( x ) f(x)w(x) f(x)w(x)的期望,从而可以近似为:
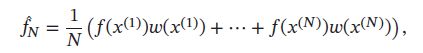
其中 x ( 1 ) , ⋯ , x ( N ) x^{(1)},\cdots,x^{(N)} x(1),⋯,x(N)为独立从 q ( x ) q(x) q(x)中随机抽取的点。
重要性采样也可以在只知道未归一化的分布 p ^ ( x ) \hat{p}(x) p^(x)的情况下计算函数 f ( x ) f(x) f(x)的期望:
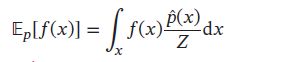
![]()
其中 w ^ ( x ) = p ^ ( x ) q ^ ( x ) , x ( 1 ) , ⋯ , x ( N ) \hat{w}(x)=\frac{\hat{p}(x)}{\hat{q}(x)},x^{(1)},\cdots,x^{(N)} w^(x)=q^(x)p^(x),x(1),⋯,x(N)为独立从 q ( x ) q(x) q(x)中随机抽取的点。
5.4 马尔科夫链蒙特卡罗方法
高维空间中,拒绝采样、重要性采样的效率随空间维数的增加而指数降低。马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)方法可以很容易地对高维变量进行采样.
MCMC方法也有很多不同的具体采样方法,核心思想是将采样过程看做一个马尔科夫链:
![]()
第 t + 1 t+1 t+1次采样依赖于第t次抽取的样本 x t \pmb{x}_t xxxt以及状态转移分布(提议分布) q ( x ∣ x t ) q(\pmb{x}|\pmb{x}_t) q(xxx∣xxxt)。如果这个马尔可夫链的平稳分布为 p ( x ) p(\pmb{x}) p(xxx),那么在状态平稳时抽取的样本就服从 p ( x ) p(\pmb{x}) p(xxx)的分布.
MCMC 方法的关键是如何构造出平稳分布为 p ( x ) p(\pmb{x}) p(xxx)的马尔可夫链,并且该马尔科夫链的状态转移分布 q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)一般为比较容易采样的分布。 x \pmb{x} xxx为离散变量时, q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)可以是一个状态转移矩阵; x \pmb{x} xxx为连续变量时, q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)可以是参数密度函数。比如各向同性的高斯分布 q ( x ∣ x ′ ) = N ( x ∣ x ′ , σ 2 I ) q(\pmb{x}|\pmb{x}^{'})=N(\pmb{x}|\pmb{x}^{'},\sigma^2I) q(xxx∣xxx′)=N(xxx∣xxx′,σ2I),其中 σ 2 \sigma^2 σ2为超参数。
使用MCMC进行采样需注意:
- 马尔科夫链需经过一段时间的随机游走才能达到平稳状态,即
预烧期(Burn-in Period)。该时期,采样点不服从分布 p ( x ) p(\pmb{x}) p(xxx),需要丢弃 - 基于马尔科夫链抽取的相邻样本高度相关,在机器学习中,一般需要样本独立同分布,故可每间隔M次随机游走,抽取一个样本,如果M足够大,可以认为抽取的样本是独立的。
5.4.1 Metropolis-Hastings 算法
Metropolis-Hastings 算法,简称MH 算法,是一种应用广泛的MCMC方法,假设马尔科夫链的状态转移分布(提议分布) q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)为一个比较容易采样的分布,其平稳分布往往不是 p ( x ) p(\pmb{x}) p(xxx)。为此,MH算法引入拒绝采样来修正提议分布,使得最终采样的分布为 p ( x ) p(\pmb{x}) p(xxx)
MH算法中,假设第t次采样的样本为 x t \pmb{x}_t xxxt,首先根据提议分布 q ( x ∣ x t ) q(\pmb{x}|\pmb{x}_t) q(xxx∣xxxt)抽取一个样本 x ^ \hat{x} x^,并以以下概率来接受 x ^ \hat{x} x^作为第 t + 1 t+1 t+1次的采样样本 x t + 1 \pmb{x}_{t+1} xxxt+1

MH算法中,因为每次 q ( x ∣ x t ) q(\pmb{x}|\pmb{x}_t) q(xxx∣xxxt)随机生成一个样本 x \pmb{x} xxx,并以上述概率的方式接受,故修正后的马尔科夫链状态转移概率为:
![]()
该修正的马尔科夫链可以达到平稳状态,且平稳分布为 p ( x ) p(\pmb{x}) p(xxx),根据马尔科夫的细致平稳条件证明如下:
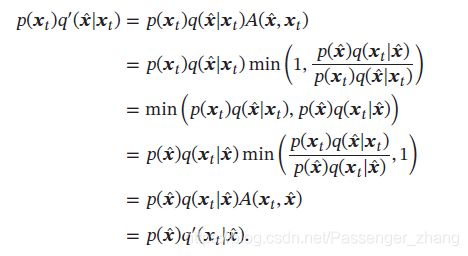
5.4.2 Metropolis 算法
如果MH算法中的提议分布式对称的,即 q ( x ^ ∣ x t ) = q ( x t ∣ x ^ ) q(\pmb{\hat{x}}|\pmb{x}_t)= q(\pmb{x}_t|\pmb{\hat{x}}) q(x^x^x^∣xxxt)=q(xxxt∣x^x^x^),第 t + 1 t+1 t+1次采样的接受率可简化为:
5.4.3 吉布斯采样
吉布斯采样(Gibbs Sampling)是一种有效对高维空间中的分布进行采样的MCMC方法,可看做Metropolis-Hastings 算法的特例,吉布斯采样采用全条件概率(Full Conditional Probability)作为提议分布来依次对每个维度进行采样,并设置接受率为 = 1.
对于一个M维的随机变量 X = [ X 1 , ⋯ , X M ] T \pmb{X}=[X_1,\cdots,X_M]^T XXX=[X1,⋯,XM]T,其第m个变量 X m X_m Xm的全条件概率为:

其中 x m = [ x 1 , ⋯ , x m − 1 , x m + 1 , ⋯ , x M ] T \pmb{x}_{\\m}=[x_1,\cdots,x_{m-1},x_{m+1},\cdots,x_M]^T xxxm=[x1,⋯,xm−1,xm+1,⋯,xM]T表示除 X m X_m Xm外其他变量的取值
吉布斯采样可按照任意顺序,根据全条件分布依次对每个变量进行采样。假设从一个随机的初始化状态 x ( 0 ) = [ x 1 ( 0 ) , ⋯ , x 1 ( M ) ] T \pmb{x}^{(0)}=[x_1^{(0)}, \cdots, x_1^{(M)}]^T xxx(0)=[x1(0),⋯,x1(M)]T开始,按照下标顺序依次对M个变量进行采样:
![]()
![]()
其中 x m ( t ) x_m^{(t)} xm(t)是第t次迭代时变量 X m X_m Xm的采样。
吉布斯采样的每单步采样也构成一个马尔科夫链,假设每个单步(采样维度为第i维)的状态转移概率 q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)为:
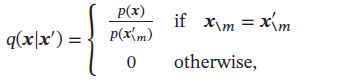
其中边际分布 p ( x m ′ ) = ∑ x m ′ p ( x ′ ) p(\pmb{x}_{\\m}^{'})=\sum_{x^{'}_m} p(\pmb{x}^{'}) p(xxxm′)=∑xm′p(xxx′),等式 x m = x m ′ \pmb{x}_{\\m}=\pmb{x}_{\\m}^{'} xxxm=xxxm′表示 x k = x k ′ , ∀ k ≠ m x_{k}=x_{k}^{'},\forall k \neq m xk=xk′,∀k=m,因此有 p ( x m ) = p ( x m ′ ) p(\pmb{x}_{\\m})=p(\pmb{x}_{\\m}^{'}) p(xxxm)=p(xxxm′),并且可以得到:
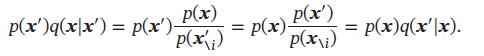
根据细致平稳条件,状态转移概率 q ( x ∣ x ′ ) q(\pmb{x}|\pmb{x}^{'}) q(xxx∣xxx′)的马尔科夫链的平稳分布为 p ( x ) p(\pmb{x}) p(xxx),随着迭代次数t的增加,样本 x ( t ) = [ x 1 ( t ) , ⋯ , x M ( t ) ] T \pmb{x}^{(t)}=[x_1^{(t)},\cdots,x_M^{(t)}]^T xxx(t)=[x1(t),⋯,xM(t)]T将收敛于概率分布 p ( x ) p(\pmb{x}) p(xxx)
6. 总结
概率图模型提供了一个用图形来描述概率模型的框架,这种可视化方法使我们可以更加容易地理解复杂模型的内在性质。
概率图模型中最基本的假设是条件独立性。
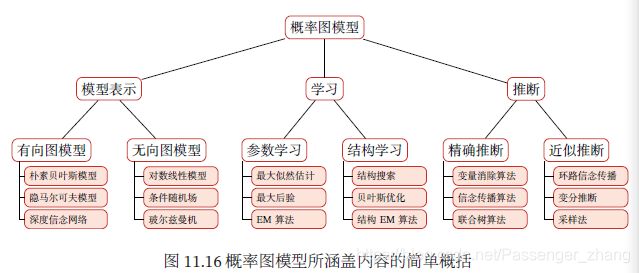
图模型和神经网络的关系 图模型和神经网络有着类似的网络结构。
图模型的节点是随机变量,其图结构的主要功能是用来描述变量之间的依赖关系,一般是稀疏连接,使用图模型可以有效进行统计推断。神经网络中的节点是神经元,是一个计算节点。
图模型中的每个变量一般有着明确的解释,变量之间依赖关系一般是人工来定义;而神经网络中的单个神经元则没有直观的解释, 如果将神经网络中每个神经元看作是一个二值随机变量,那神经网络就变成一个Sigmoid 信念网络.
神经网络是判别模型,直接用来分类。图模型不但可以是判别模型,也可以是生成模型。 生成模型不但可以用来生成样本,也可以通过贝叶斯公式用来做分类。
图模型的参数学习的目标函数为似然函数或条件似然函数,若包含隐变量则通常通过EM 算法来求解。而神经网络参数学习的目标函数为交叉熵或平方误差等损失函数.