李宏毅DLHLP.07.Speech Recognition.6/7. RNN-T Training
文章目录
- 介绍
- How to sum over all the alignments
- Training
-
- 第一项
- 第二项
- Testing (Inference, decoding)
- 小结
- 参考资料
介绍
本门课程是2020年李宏毅老师新课:Deep Learning for Human Language Processing(深度学习与人类语言处理)
课程网站:http://speech.ee.ntu.edu.tw/~tlkagk/courses_DLHLP20.html
B站视频:https://www.bilibili.com/video/BV1EE411g7Uk?t=222
公式输入请参考:在线Latex公式
上节提到解决alignments有四个问题:
如何穷举所有的alignments:1. Enumerate all the possible alignments
如何累加所有的alignments:2. How to sum over all the alignments
3.如何训练CTC,RNN-T,CTC,RNN-T是NN,需要用反向传播(GD)求解,也就是要求导,即:
θ ∗ = a r g max θ l o g P θ ( Y ^ ∣ X ) \theta^*=arg\underset{\theta}{\text{max}}logP_{\theta}(\hat Y|X) θ∗=argθmaxlogPθ(Y^∣X)
要求导:
∂ P θ ( Y ^ ∣ X ) ∂ θ = ? \cfrac{\partial P_{\theta}(\hat Y|X)}{\partial \theta}=? ∂θ∂Pθ(Y^∣X)=?
4.如何测试Testing (Inference, decoding): 就是要解:
Y ∗ = a r g max Y l o g P ( Y ∣ X ) Y^*=arg\underset{Y}{\text{max}}logP(Y|X) Y∗=argYmaxlogP(Y∣X)
上节讲了第一个。
下面继续讲第二个问题:
How to sum over all the alignments
这部分内容比较难,用的RNN-T做为例子,CTC原理是一样的。先看上节课提到过的例子:
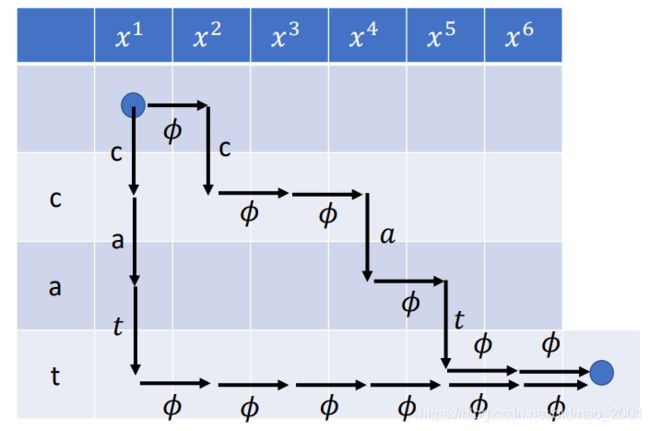
我们观察上面的那个路径(alignments):
h = ϕ c ϕ ϕ a ϕ t ϕ ϕ h=\phi c\phi\phi a\phi t\phi\phi h=ϕcϕϕaϕtϕϕ
那么上面这个alignment出现的概率计算方法为:(先算 ϕ \phi ϕ出现在句首的几率,在计算句首产生 ϕ \phi ϕ条件下,c产生的几率,以此类推)
P ( h ∣ X ) = P ( ϕ ∣ X ) × P ( c ∣ X , ϕ ) × P ( ϕ ∣ X , ϕ c ) . . . . . . P(h|X)=P(\phi|X)\times P(c|X,\phi)\times P(\phi|X,\phi c)... ... P(h∣X)=P(ϕ∣X)×P(c∣X,ϕ)×P(ϕ∣X,ϕc)......
RNN-T先读取第一个acoustic feature,然后通过encoder,变成一个vector的形式: h 1 h^1 h1
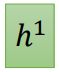
RNN-T还有一个RNN结构(下面的方形),专门吃encoder产生的token,产生结果对后面的输出产生影响,由于是刚开始,encoder没有产生token,我们设置一个BOS作为RNN的输入
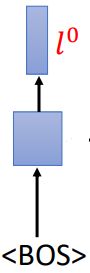
得到一个结果: l 0 l^0 l0。
然后我们把 h 1 h^1 h1和 l 0 l^0 l0都丢到Decoder中去,得到概率分布: p 1 , 0 p_{1,0} p1,0
下标1代表吃第一个acoustic feature,下标0代表已经产生0个token的概率分布。

那么 ϕ \phi ϕ出现在句首的概率是从概率分布: p 1 , 0 p_{1,0} p1,0中产生 ϕ \phi ϕ的几率。

有了 ϕ \phi ϕ之后,再看生成c的几率:
这个 ϕ \phi ϕ对于RNN结构而言不会产生影响,RNN结构只处理token
对于Decoder而言,遇到 ϕ \phi ϕ之后,它就知道这个acoustic feature的信息已用尽,要读取下一个acoustic feature,于是encoder再读取第二个acoustic feature,并得到对应的vector: h 2 h^2 h2,由于RNN结构的 l 0 l^0 l0不变,因此Decoder吃 h 2 h^2 h2和 l 0 l^0 l0得到概率分布: p 2 , 0 p_{2,0} p2,0
这里的下标代表读取到第二个acoustic feature,已产生0个token的概率分布
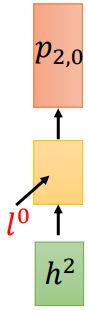
然后在句首产生 ϕ \phi ϕ条件下,c产生的概率就是从概率分布: p 2 , 0 p_{2,0} p2,0取到c的概率。
接下来算出现 ϕ c \phi c ϕc后,出现 ϕ \phi ϕ 的几率,这个时候由于产生了token,RNN结构就会根据token c产生第二个结果: l 1 l^1 l1
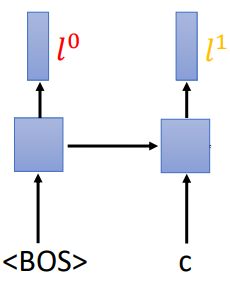
在Decoder的部分,由于没有看到 ϕ \phi ϕ,因此输入还是 h 2 h^2 h2

这个时候Decoder产生的概率分布为: p 2 , 1 p_{2,1} p2,1
下标表示第二个acoustic feature参数,已经产生第1个token的概率分布。
出现 ϕ c \phi c ϕc后,出现 ϕ \phi ϕ 的几率就是从概率分布: p 2 , 1 p_{2,1} p2,1取到 ϕ \phi ϕ 的概率。
下面就按上面的模式不断重复:
RNN结构的处理结果:

Decoder的处理结果:
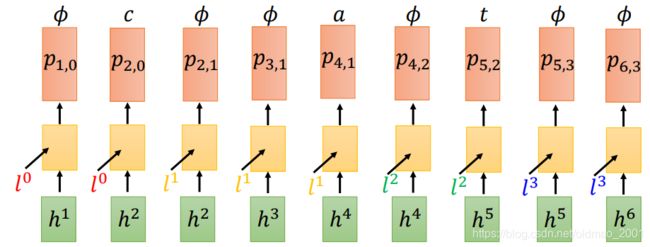
最后的计算就是把所有最上面从概率分布中取出对应的alignments的几率,并且相乘起来:

重点:
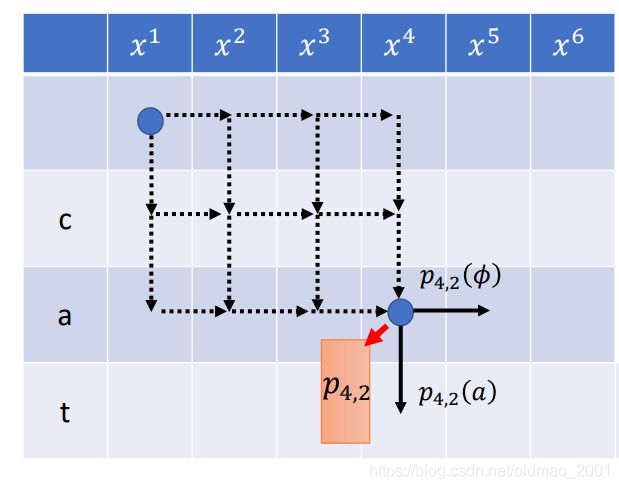
注意观察上图,上图中的每一个格子其实都是对应一个概率分布,就是前面讲的 p i , j p_{i,j} pi,j,i代表第几个acoustic feature,这里是 x i x^i xi,上面讲用的是 h i h^i hi,其实都是一样,后者是前者经过encoder得到的结果。j代表当前已经产生了几个token。
这里的每个格子的概率分布 p i , j p_{i,j} pi,j是固定的,与如何走到该格子的路径无关。
这里的每个格子的概率分布 p i , j p_{i,j} pi,j是固定的,与如何走到该格子的路径无关。
这里的每个格子的概率分布 p i , j p_{i,j} pi,j是固定的,与如何走到该格子的路径无关。
所以上图中无论怎么从虚线走到 p 4 , 2 p_{4,2} p4,2, p 4 , 2 p_{4,2} p4,2是固定的,下面看一下这个如何理解:
上面讲了,RNN-T中的RNN结构是不吃NULL的,只吃token,所以NULL在什么位置并不会影响RNN结构的输出,例如下面三种序列,RNN的输出都是一样的。都会输出 l 2 l^2 l2
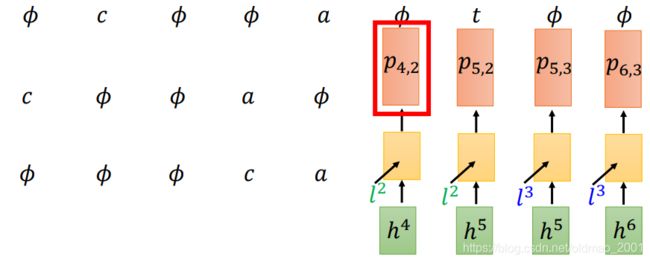
而acoustic feature的输入只和NULL的个数有关,有三个NULL就会输入 h 4 h^4 h4,和NULL的位置也没有关系。
理解这个了之后,就可以开始算概率和了。
记: α i , j \alpha_{i,j} αi,j为the summation of the scores of all the alignments that read i-th acoustic features and output j-th tokens
然后我们就可以把 α i , j \alpha_{i,j} αi,j对应到每个格子,例如:

这里的 α 4 , 2 \alpha_{4,2} α4,2意思是将四个acoustic feature产生的alignments和产生两个token的alignments的概率累加起来。具体而言 α 4 , 2 \alpha_{4,2} α4,2怎么求?
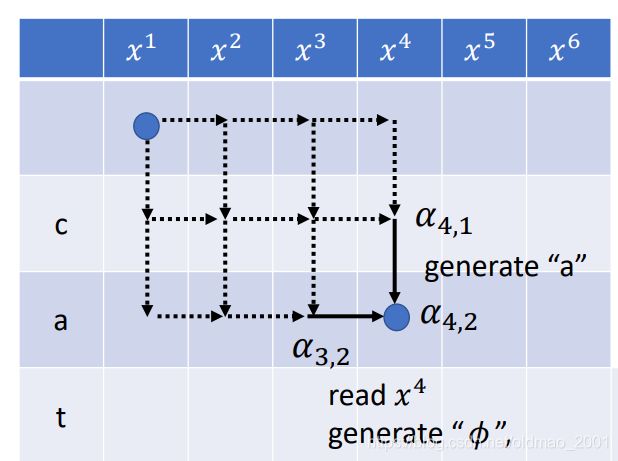
α 4 , 2 \alpha_{4,2} α4,2可以由 α 4 , 1 \alpha_{4,1} α4,1和 α 3 , 2 \alpha_{3,2} α3,2两个状态过来:
α 4 , 1 \alpha_{4,1} α4,1是已经读取了四个acoustic feature,已经产生了一个token,还需要再生成一个token:a,就变成了 α 4 , 2 \alpha_{4,2} α4,2;
α 3 , 2 \alpha_{3,2} α3,2是已经读取了三个acoustic feature,已经产生了两个token,还需要再读取一个acoustic feature: x 4 x^4 x4,就变成了 α 4 , 2 \alpha_{4,2} α4,2。
计算公式为:
α 4 , 2 = α 4 , 1 p 4 , 1 ( a ) + α 3 , 2 p 3 , 2 ( ϕ ) \alpha_{4,2}=\alpha_{4,1}p_{4,1}(a)+\alpha_{3,2}p_{3,2}(\phi) α4,2=α4,1p4,1(a)+α3,2p3,2(ϕ)
那么最右下角的 α i , j \alpha_{i,j} αi,j就是对应的alignments的总和,也就是要算每个格子对应的 α \alpha α

第三个问题:
Training
θ ∗ = a r g max θ l o g P θ ( Y ^ ∣ X ) \theta^*=arg\underset{\theta}{\text{max}}logP_{\theta}(\hat Y|X) θ∗=argθmaxlogPθ(Y^∣X)
要求导:
∂ P θ ( Y ^ ∣ X ) ∂ θ = ? \cfrac{\partial P_{\theta}(\hat Y|X)}{\partial \theta}=? ∂θ∂Pθ(Y^∣X)=?
经过第二个问题的学习,我们知道了:
P ( Y ^ ∣ X ) = ∑ h P ( h ∣ X ) P(\hat Y|X)=\sum_hP(h|X) P(Y^∣X)=h∑P(h∣X)
上式中的h是由一连串的概率相乘得来
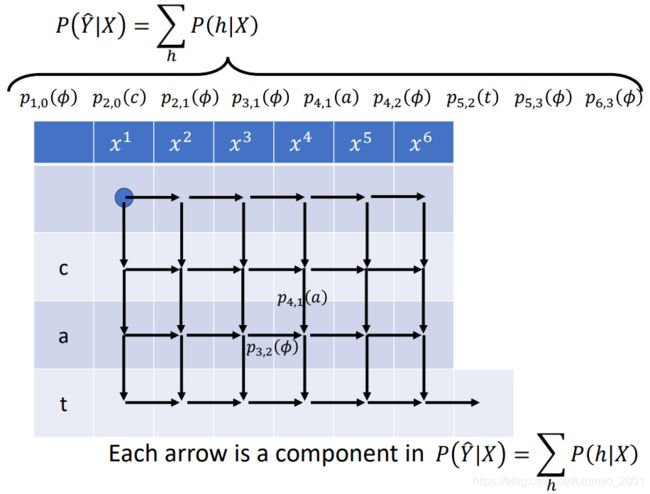
所以整个式子就是一连串token产生的概率相乘后相加得来。
这些概率都是受到参数 θ \theta θ的影响,然后概率有去影响我们要计算的总概率
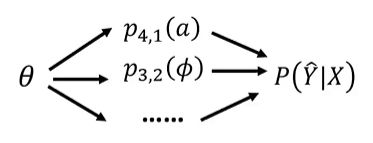
根据链式法则:
∂ P θ ( Y ^ ∣ X ) ∂ θ = ∂ p 4 , 1 ( a ) ∂ θ P θ ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) + ∂ p 3 , 2 ( ϕ ) ∂ θ P θ ( Y ^ ∣ X ) ∂ p 3 , 2 ( ϕ ) + . . . \cfrac{\partial P_{\theta}(\hat Y|X)}{\partial \theta}=\cfrac{\partial p_{4,1}(a)}{\partial\theta}\cfrac{P_{\theta}(\hat Y|X)}{\partial p_{4,1}(a)}+\cfrac{\partial p_{3,2}(\phi)}{\partial\theta}\cfrac{P_{\theta}(\hat Y|X)}{\partial p_{3,2}(\phi)}+... ∂θ∂Pθ(Y^∣X)=∂θ∂p4,1(a)∂p4,1(a)Pθ(Y^∣X)+∂θ∂p3,2(ϕ)∂p3,2(ϕ)Pθ(Y^∣X)+...
下面来看 θ \theta θ对上图中每个箭头的偏导怎么求。
第一项
∂ p 4 , 1 ( a ) ∂ θ \cfrac{\partial p_{4,1}(a)}{\partial\theta} ∂θ∂p4,1(a)
把 θ \theta θ看做下面这个网络的参数, p 4 , 1 p_{4,1} p4,1是输出的一个概率分布,从NN的角度来说,就是求反向传播就可以得到偏导结果。这里不展开。

第二项
下面再来看另外一项偏导如何求,例如:
P θ ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) \cfrac{P_{\theta}(\hat Y|X)}{\partial p_{4,1}(a)} ∂p4,1(a)Pθ(Y^∣X)
我们看它的分母是一个求和项,可以看做是带有 p 4 , 1 ( a ) p_{4,1}(a) p4,1(a)的alignments项和不带有 p 4 , 1 ( a ) p_{4,1}(a) p4,1(a)的alignments项的求和。
P θ ( Y ^ ∣ X ) = ∑ h P ( h ∣ X ) = ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) + ∑ h w i t h o u t p 4 , 1 ( a ) P ( h ∣ X ) P_{\theta}(\hat Y|X)=\sum_hP(h|X)=\sum_{h\space with\space p_{4,1}(a)}P(h|X)+\sum_{h\space without\space p_{4,1}(a)}P(h|X) Pθ(Y^∣X)=h∑P(h∣X)=h with p4,1(a)∑P(h∣X)+h without p4,1(a)∑P(h∣X)
求偏导的时候,后面那项不用考虑,为0,然后前面那项我们可以写成:
∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) = ∑ h w i t h p 4 , 1 ( a ) p 4 , 1 ( a ) × o t h e r \sum_{h\space with\space p_{4,1}(a)}P(h|X)=\sum_{h\space with\space p_{4,1}(a)}p_{4,1}(a)\times other h with p4,1(a)∑P(h∣X)=h with p4,1(a)∑p4,1(a)×other
那么:
∑ h w i t h p 4 , 1 ( a ) o t h e r = ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) p 4 , 1 ( a ) = 1 p 4 , 1 ( a ) ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) \sum_{h\space with\space p_{4,1}(a)}other=\sum_{h\space with\space p_{4,1}(a)}\cfrac{P(h|X)}{p_{4,1}(a)}=\cfrac{1}{p_{4,1}(a)}\sum_{h\space with\space p_{4,1}(a)}P(h|X) h with p4,1(a)∑other=h with p4,1(a)∑p4,1(a)P(h∣X)=p4,1(a)1h with p4,1(a)∑P(h∣X)
p 4 , 1 ( a ) × o t h e r p_{4,1}(a)\times other p4,1(a)×other对 p 4 , 1 ( a ) p_{4,1}(a) p4,1(a)求偏导就剩下other(这块不懂说明你高数基本求导没学好。。。就是: a x ′ = a ax'=a ax′=a)
所以最后:
P θ ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) = ∑ h w i t h p 4 , 1 ( a ) o t h e r = 1 p 4 , 1 ( a ) ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) \cfrac{P_{\theta}(\hat Y|X)}{\partial p_{4,1}(a)}=\sum_{h\space with\space p_{4,1}(a)}other=\cfrac{1}{p_{4,1}(a)}\sum_{h\space with\space p_{4,1}(a)}P(h|X) ∂p4,1(a)Pθ(Y^∣X)=h with p4,1(a)∑other=p4,1(a)1h with p4,1(a)∑P(h∣X)
搞定。
下面记: β i , j \beta_{i,j} βi,j
the summation of the score of all the alignments staring from i-th acoustic features and j-th tokens.
就是从当前位置到结束位置所有alignments 概率之和。
例如下图中:
β 4 , 2 = β 4 , 3 p 4 , 2 ( t ) + β 5 , 2 p 4 , 2 ( ϕ ) \beta_{4,2}=\beta_{4,3}p_{4,2}(t)+\beta_{5,2}p_{4,2}(\phi) β4,2=β4,3p4,2(t)+β5,2p4,2(ϕ)
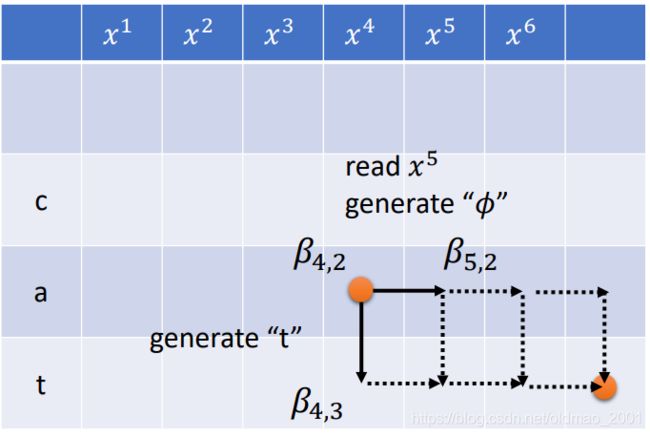
有了 α , β \alpha,\beta α,β后,就可以算所有包含某个(i,j)位置的alignments路径概率总和。同样以 p 4 , 1 p_{4,1} p4,1为例
P θ ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) = 1 p 4 , 1 ( a ) ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) = 1 p 4 , 1 ( a ) α 4 , 1 p 4 , 1 ( a ) β 4 , 2 = α 4 , 1 β 4 , 2 \cfrac{P_{\theta}(\hat Y|X)}{\partial p_{4,1}(a)}=\cfrac{1}{p_{4,1}(a)}\sum_{h\space with\space p_{4,1}(a)}P(h|X)=\cfrac{1}{p_{4,1}(a)}\alpha_{4,1}p_{4,1}(a)\beta_{4,2}=\alpha_{4,1}\beta_{4,2} ∂p4,1(a)Pθ(Y^∣X)=p4,1(a)1h with p4,1(a)∑P(h∣X)=p4,1(a)1α4,1p4,1(a)β4,2=α4,1β4,2

也就是有了 α , β \alpha,\beta α,β后,可以把整个第二项算出来,联合第一项就可以完成整个求偏导的过程,从而完成训练。
Testing (Inference, decoding)
Y ∗ = a r g max Y l o g P ( Y ∣ X ) Y^*=arg\underset{Y}{\text{max}}logP(Y|X) Y∗=argYmaxlogP(Y∣X)
理想上求使得Y最大公式为:
a r g max Y l o g ∑ h ∈ a l i g n ( Y ) P ( h ∣ X ) arg\underset{Y}{\text{max}}log\sum_{h\in align(Y)}P(h|X) argYmaxlogh∈align(Y)∑P(h∣X)
这个公式要计算所有alignment的可能,并求和,不是不能求,特别麻烦,老师也没给具体方法。
现在有一个近似公式:
a r g max Y max h ∈ a l i g n ( Y ) l o g P ( h ∣ X ) arg\underset{Y}{\text{max}}\underset{h\in align(Y)}{\text{max}}logP(h|X) argYmaxh∈align(Y)maxlogP(h∣X)
就是不穷举所有的alignment序列h,而是找一个使得几率P最大的那个alignment序列 h ∗ h^* h∗来替换掉求和。
h ∗ = a r g max Y l o g P ( h ∣ X ) h^*=arg\underset{Y}{\text{max}}logP(h|X) h∗=argYmaxlogP(h∣X)
其 中 P ( h ∣ X ) = P ( h 1 ∣ X ) P ( h 2 ∣ X , h 1 ) P ( h 3 ∣ X , h 1 , h 2 ) . . . 其中P(h|X)=P(h_1|X)P(h_2|X,h_1)P(h_3|X,h_1,h_2)... 其中P(h∣X)=P(h1∣X)P(h2∣X,h1)P(h3∣X,h1,h2)...
h是alignment序列:
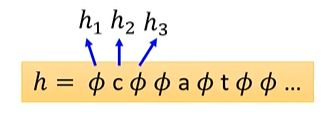
然后再根据alignment序列 h ∗ h^* h∗求最大的 Y ∗ Y^* Y∗
实操的时候是用RNN-T中Decoder生成的概率分布中几率最大那个结果拿出来组合为 h ∗ h^* h∗

当然,使用各个概率分布的最大值进行相乘得到的结果不一定最优,可以用
Beam Search来做。这里不展开。
小结
| LAS | CTC | RNN-T | |
|---|---|---|---|
| Decoder | dependent | independent | dependent |
| Alignment | not explicit(soft alignment) | Yes | Yes |
| Training | just train it | sum over alignment | sum over alignment |
| On-line | No | Yes | Yes |
参考资料
• [Yu, et al., INTERSPEECH’16] Dong Yu, Wayne Xiong, Jasha Droppo, Andreas Stolcke , Guoli Ye, Jinyu Li , Geoffrey Zweig, Deep Convolutional Neural Networks with Layer-wise Context Expansion and Attention, INTERSPEECH, 2016
• [Saon, et al., INTERSPEECH’17] George Saon, Gakuto Kurata, Tom Sercu, Kartik Audhkhasi, Samuel Thomas, Dimitrios Dimitriadis, Xiaodong Cui, Bhuvana Ramabhadran, Michael Picheny, Lynn-Li Lim, Bergul Roomi, Phil Hall, English Conversational Telephone Speech Recognition by Humans and Machines, INTERSPEECH, 2017
• [Povey, et al., ICASSP’10] Daniel Povey, Lukas Burget, Mohit Agarwal, Pinar Akyazi, Kai Feng, Arnab Ghoshal, Ondrej Glembek, Nagendra Kumar Goel, Martin Karafiat, Ariya Rastrow, Richard C. Rose, Petr Schwarz, Samuel Thomas, Subspace Gaussian Mixture Models for speech recognition, ICASSP, 2010
• [Mohamed , et al., ICASSP’10] Abdel-rahman Mohamed and Geoffrey Hinton, Phone recognition using Restricted Boltzmann Machines, ICASSP, 2010