因果推论 (Causal Inference)
This is the sixth post on the series we work our way through “Causal Inference In Statistics” a nice Primer co-authored by Judea Pearl himself.
这是本系列的第六篇文章，我们将通过Judea Pearl本人与他人合着的《引诱统计学中的因果关系》一书进行介绍。
You can find the previous post here and all the we relevant Python code in the companion GitHub Repository:
您可以在此处找到相关的上一篇文章以及相关的GitHub存储库中所有与我们相关的Python代码：
While I will do my best to introduce the content in a clear and accessible way, I highly recommend that you get the book yourself and follow along. So, without further ado, let’s get started!
尽管我会尽力以清晰易懂的方式介绍内容，但我强烈建议您自己拿书并继续学习。 因此，事不宜迟，让我们开始吧！
In the previous post V, we started on Chapter II of the book where Pearl starts to build up the machinery of Causal Inference. In this post we look at Colliders, one of the most powerful ideas in the analysis of graphical models.
在上一篇文章V中 ，我们从书的第二章开始，Pearl开始建立因果推理的机制。 在这篇文章中，我们看一下碰撞器，它是图形模型分析中最强大的想法之一。
2.3对撞机 (2.3 Colliders)
The third, and perhaps the most important, graph motif that we will cover is known as the Collider and is illustrated in this figure:
我们将介绍的第三个(也许是最重要的)图形图案称为Collider，如下图所示：
Collider nodes are nodes that receive inputs from 2 or more other variables. Applying the rules we are already familiar with, we can immediately conclude:
对撞机节点是从2个或更多其他变量接收输入的节点。 应用我们已经熟悉的规则，我们可以立即得出结论：
X and Z are dependent — P(X|Z) ≠ P(X)
X和Z是依赖的 -P(X | Z)≠P(X)
Y and Z are dependent — P(Y|Z) ≠ P(Y)
Y和Z是依赖的 -P(Y | Z)≠P(Y)
X and Y are independent — P(X|Y) =P(X)
X和Y是独立的 -P(X | Y)= P(X)
X and Y are dependent conditional on Z — P(X|Y, Z) ≠ P(X|Z)
X和Y取决于Z — P(X | Y，Z)≠P(X | Z)
Points 1 and 2 follow directly from Rule 0: Any two variables with a directed edge between them are dependent. Point 3 is obvious from the fact that there is no directed path between X and Y (neither is an ancestor or a descendent of the other).
点1和2直接从规则0得出：在它们之间有向边的任何两个变量都是相关的。 从X和Y之间没有定向路径的事实可以明显看出第3点(两者都不是祖先或后代)。
Point 4 is the most interesting case, but it can be understood with a simple algebraic example. Consider the mathematical expression:
点4是最有趣的情况，但是可以通过一个简单的代数示例来理解。 考虑一下数学表达式：
This relationship determines the value of Z and is valid for any possible value of X and Y, but as soon as I fix the value of Z, say Z=10 that immediately limits the possible values of X and Y that are now constrained such that, Y = 10-Z (or, graphically, lie on the intersection of the two Z=X+Y and Z=10 planes):
此关系确定Z的值，并且对于X和Y的任何可能值均有效，但是一旦我确定Z的值，则说Z = 10立即限制了现在受约束的X和Y的可能值，从而，Y = 10-Z(或以图形方式位于两个Z = X + Y和Z = 10平面的交点上)：
This is a simple illustration of the most fundamental definition of conditioning: filtering by the value of the conditioning variable.
这是对调节的最基本定义的简单说明：通过调节变量的值进行过滤。
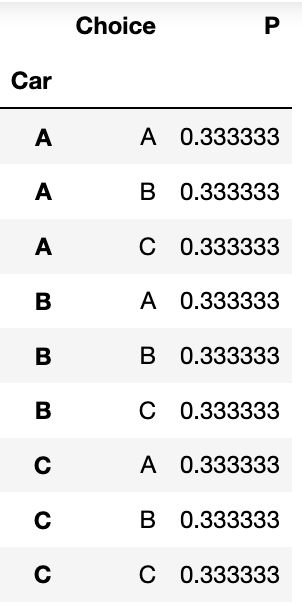
The book further illustrates this idea using the example of the well known Monty-Hall problem. For this game, our probability table would be:
本书以著名的蒙蒂·霍尔(Monty-Hall)问题为例进一步说明了这一想法。 对于这个游戏，我们的概率表将是：
Where the 0.0555 values correspond to the fact that we give Monty a 50/50 chance of choosing either goat if I happen to choose the door where the car is.
0.0555的值对应的事实是，如果我碰巧选择了汽车所在的门，我们给Monty 50/50的机会选择任一只山羊。
From this table, it’s easy to see that P(Choice|Car)=P(Car), or, in other words:
从此表中，很容易看出P(Choice | Car)= P(Car)，或者换句话说：
Essentially, I’m choosing one of the three doors at random. Now, let’s take a look at P(Choice | Car, Monty):
本质上，我是随机选择三个门之一。 现在，让我们看一下P(Choice | Car，Monty)：
Where it is now clear that depending on the door that Monty has chosen, the value of P(Choice | Car) will change.
现在很明显，根据Monty选择的门，P(Choice | Car)的值将改变。
This is also a clear example of a non-causal dependency between two variables, illustrating the point that correlation does not imply causation. Here the relationship between the two variables (Car and Choice) comes about just due to the fact that we limited our space of possibilities by adding the extra information about Monty’s choice. An event that is already familiar to us from our discussion of Bayes Theorem.
这也是两个变量之间的非因果关系的一个清晰示例，说明了相关性并不意味着因果关系。 在这里，这两个变量(汽车和选择)之间的关系恰好是由于我们通过添加有关蒙蒂选择的额外信息来限制可能性的事实。 通过贝叶斯定理的讨论，我们已经很熟悉这一事件。
From these examples, it is easy to extract a new general rule:
从这些示例中，很容易提取出一条新的通用规则：
Rule 3 (Conditional Independence in Colliders): If a variable Z is the collision node between two variables X and Y, and there is only one path between X and Y, then X and Y are unconditionally independent but are dependent conditional on Z and any descendents of Z.
规则3(碰撞者的条件独立性)：如果变量Z是两个变量X和Y之间的碰撞节点，并且X和Y之间只有一条路径，则X和Y是无条件独立的，但取决于Z和任何其他条件Z的后代。
Congratulations on following along yet another blog post on this series series. I sincerely hope that you continue to enjoy reading them as much as I enjoy writing them.
祝贺您关注本系列文章的另一篇博客文章。 我衷心希望您继续喜欢阅读它们，就像我喜欢写它们一样。
Just a quick reminder that you can find the code for all the examples above in our GitHub repository:
谨在此提醒您，您可以在我们的GitHub存储库中找到上述所有示例的代码：
And if you would like to be notified when the next post comes out, you can subscribe to the The Sunday Briefing newsletter:
而且，如果您希望在下一篇文章发表时得到通知，可以订阅《星期日简报》时事通讯：
翻译自: https://medium.com/data-for-science/causal-inference-part-vi-colliders-af07301c9a15