python学习笔记_第26天（数据结构与算法）

常见时间复杂度

执行次数函数举例	阶	非正式术语
12	O(1)	常数阶
2n+3	O(n)	线性阶
3n2+2n+1	O(n2)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n3+2n2+3n+4	O(n3)	立方阶
2n	O(2n)	指数阶

ps：经常将log2n（以2为底的对数）简写成logn

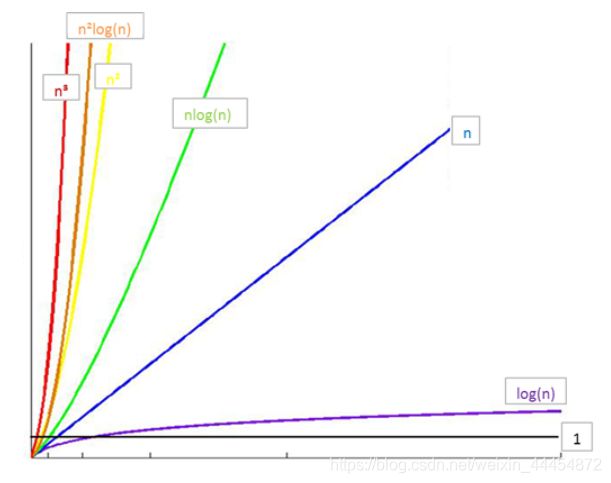
所消耗的时间从小到大：
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

Python内置类型性能分析

• timeit模块
  timeit模块用来测试一小段Python代码的执行速度，测量小段代码执行速度的类。
  class timeit.Timer(stmt=‘pass’, setup=‘pass’, timer=)
  stmt – 要测试的代码语句(statment)，传输的是字符串需带‘’
  setup – 运行代码时需要的前期准备设置(如import 模块)，传输的是字符串需带‘’
  timer – 一个定时器函数，与系统平台有关
• timeit.Timer.timeit方法
  方法返回执行代码的平均耗时，一个float类型的秒数。
  timeit.Timer.timeit(number=1000000)
  timeit – Timer类中测试语句执行速度的对象方法
  number – 测试代码时的测试次数，默认为1000000次

list的操作测试

- 列表生成的四种方法：
1、已存在列表组合成新列表，如[]+[]或[].extend([])
两列表相加生成的新列表是一个新对象，在空间上有消耗；列表.extend(列表)，直接在原对象上追加新列表，不生成新对象占用空间

from timeit import Timer
def t1():
    l = []
    for i in range(1000):
        l = l + [i]


def t2():
    l = []
    for i in range(1000):
        l.extend([i])
        
time1 = Timer("t1()", "from __main__ import t1")  # 参数传入的是字符串，要用''框起来
print("+：", time1.timeit(number=1000), "seconds")  # timeit.Timer.timeit(number=1000000)，单位为秒
time2 = Timer("t2()", "from __main__ import t2")
print("extend：", time2.timeit(number=1000), "seconds")

2、列表生成器生成列表，如[ x for x in range(100)]

def t3():
    l = [i for i in range(1000)]
    
time3 = Timer("t3()", "from __main__ import t3")
print("[i for i in range]", time3.timeit(number=1000), "seconds")

3、通过可迭代对象转换成列表，如list(range(100))

def t4():
    l = list(range(1000))

time4 = Timer("t4()", "from __main__ import t4")
print("list range ", time4.timeit(number=1000), "seconds")

4、创建空列表后逐一追加数据或插入数据，如[].append或[].insert(索引,数据)
append()接收单个元素，extend()接收单个列表或可遍历的对象
append对列表尾部追加数据，insert(索引,追加数据)向列表指定位置插入数据

def t5():
    l = []
    for i in range(1000):
        l.append(i)  # 在列表末尾追加新数据


def t6():
    l = []
    for i in range(1000):
        l.insert(0, i)  # 指定在列表开头追加新数据

time5 = Timer("t5()", "from __main__ import t5")
print("append：", time5.timeit(number=1000), "seconds")
time6 = Timer("t6()", "from __main__ import t6")
print("insert：", time6.timeit(number=1000), "seconds")

执行结果：
+： 1.2755570999999999 seconds
extend： 0.11991869999999993 seconds
[i for i in range] 0.040143599999999946 seconds
list range 0.013012400000000035 seconds
append： 0.07990540000000013 seconds
insert： 0.3247659999999999 seconds

两列表相加生成新列表即耗时又耗空间，一般不用。
insert指定位置追加会比直接尾部追加耗时更多，因为list类型与dict类型不能简单算作基本数据类型，是Python分装好的数据集合，是一个容器。

• list内置操作的时间复杂度

操作	说明	时间复杂度
indexx[]	索引方式取值	O(1)
index assignment	索引方式赋值	O(1)
append	尾部追加	O(1)
pop()	尾部弹出	O(1)
pop(i)	指定位置弹出，n为列表长度	O(n)，最坏时间复杂度
insert(i,item)	指定位置插入，n为列表长度	O(n)，最坏时间复杂度
del operator	删除元素每个元素 ，n为列表长度	O(n)
iteration	迭代，n为列表长度	O(n)
contains(in)	判断列表是否包含魔元素，n为列表长度	O(n)，最坏时间复杂度
get slice[x:y]	取切片	O(k)，k=y-x
del slice	删除切片，切片后方元素前移 ，n为列表长度	O(n)，最坏时间复杂度
set slice	设置切片，先执行删除切片，后对删除部分切片赋值，k为切片长度，n为列表长度	O(n+k)，最坏时间复杂度
reverse	倒置列表	O(n)
concatenate	对列表后方添加一列表，k为添加列表的长度	O(k)
sort	排序	O(n log n)
multiply	重复，k为重复次数，n为重复的列表长度	O(nk)

• dict内置操作的时间复杂度

操作	说明	时间复杂度
copy	复制字典	O(n)
get item	取值，键唯一，通过建取值	O(1)
set item	设置，键唯一，通过建设置	O(1)
delete item	删除，键唯一，通过建删除
contains(in)	包含，键唯一，通过建取查找	O(1)
iteration	迭代	O(n)

数据结构

假设用列表和字典来存储一个班的学生信息。想要在列表中获取一名同学的信息时，需要遍历这个列表，其时间复杂度为O(n)；而使用字典存储时，可将学生姓名作为字典的键，学生信息作为值，进而查询时不需要遍历便可快速获取到学生信息，其时间复杂度为O(1)。
为了解决问题，需要将数据保存下来，然后根据数据的存储方式来设计算法进行处理，那么数据的存储方式不同就会导致需要不同的算法。算法解决问题的效率越快越好，就需要考虑数据究竟如何保存的问题，这就是数据结构。

• 概念
  数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型（int，float，char等）。数据元素之间不是独立的，存在特定的关系，这种关系就是结构。数据结构指数据对象中数据元素之间的关系。
  Python中提供了很多系统自己定义好现成的数据结构类型，Python的内置数据结构有列表、元组、字典等。一些Python系统里面没有直接定义的数据组织方式，需要自定义实现，这些数据组织方式称之为Python的扩展数据结构，如栈，队列等。

算法与数据结构的区别

• 数据结构只是静态的描述了数据元素之间的关系。
• 高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法；即算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体。

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。
引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

• 最常用的数据运算有五种：
  插入
  删除
  修改
  查找
  排序