【统计学习方法算法实现】一、感知机学习算法 2. 对偶形式

《统计学习方法》——算法实现

一、感知机学习算法

2. 对偶形式

对偶形式的基本想法是，将$w$和$b$表示为实例$x_i$和标记$y_i$的线性组合的形式，通过求解其系数而求得$w$和$b$。不失一般性，在原始形式算法中，可假设初始值$w_0$，$b_0$均为0，对误分类点$(x_i,y_i)$通过$$w\leftarrow w+\eta y_i{x}_i$$ $$b\leftarrow b+\eta y_i$$
逐步修改$w$，$b$，设修改$n$次，则$w$，$b$关于$(x_i,y_i)$的增量分别是${\alpha }_i{y}_i{x}_i$和${\alpha }_i{y}_i$，这里${\alpha }_i=n_i\eta$。这样，从学习过程不难看出，最后学习到的$w$，$b$可以分别表示为$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$$$b=\sum _{i=1}^N{\alpha }_i{y}_i$$
这里，${\alpha }_i\ge 0$，$i=1,2,\cdots ,N$，当$\eta =1$时，表示第$i$个实例点由于误分类而进行更新的次数。实例点更新次数越多，意味着它距离分类超平面越近，也就越难正确分类。 换句话说，这样的实例对学习结果影响最大。
下面对照原始形式来叙述感知机学习算法的对偶形式。

---

输入：线性可分的数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$，其中$x_i\in R^n$，$y_i\in \{-1,+1\}$，$i=1,2,\cdots ,N$；学习率$\eta (0<\eta \le 1)$；
输出：$\alpha$，$b$；感知机模型$f(x)=sign({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b)$，其中$\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N{)}^T$。
(1) $\alpha \leftarrow 0$，$b\leftarrow 0$；
(2) 在训练集中选取数据$(x_i,y_i)$；
(3) 如果$y_i({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x_i+b)\le 0$，$${\alpha }_i\leftarrow {\alpha }_i+\eta$$ $$b\leftarrow b+\eta y_i$$
(4) 转至(2)直到没有误分类数据

---

对偶性是中训练实例仅以内积的形式出现。为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵$$G=[x_i\cdot x_j{]}_{N\times N}$$

算法实现

之前的数据准备以及数据可视化同之前相同，所以直接把代码放在这里：

from matplotlib import pyplot as plt
import pandas as pd
import numpy as np

data = pd.read_excel('data.xlsx')  # 读取点数据
label = pd.read_excel('label.xlsx')  # 读取分类标签

# 将两者读取到numpy数组当中，可进行相应数值操作
x = data.values
y = label.values

# 可视化
plt.title('Data Visualization')  # 标题
plt.xlim((0, 5))  # 设置x坐标轴范围
plt.ylim((0, 5))  # 设置y坐标轴范围
map_color = {
     -1: 'r', 1: 'b'}  # 类别及其对应点颜色的映射
color = []
for dot in y:
    color += map_color[dot[0]]
plt.scatter(x[:, 0], x[:, 1], c=color)
plt.show()

首先需要一个函数来检查是否所有点被正确分类，并返回误分类点的索引列表。

def check():
    """"检查是否所有误分类点都分类正确，返回误分类索引"""
    error = []
    for i in range(x.shape[0]):
        s = 0
        for j in range(x.shape[0]):
            s += alpha[j] * y[j] * G[j][i]
        if y[i] * (s + b) <= 0:
            error.append(i)
    return error

然后根据所给出的算法进行学习，同样权值初始化不同和选取的误分类点不同结果也不同：

# 感知机学习
alpha = np.zeros(x.shape[0])  # 每一个数据点都有一个对应的值
b = 0
eta = 1
# 计算Gram矩阵
G = np.matmul(x, x.T)
# 开始学习
wrong = check()
time = 1  # 计步器
while len(wrong) != 0:  # 有误分类点
    ind = wrong[np.random.randint(0, len(wrong))]  # 随机选择一个误分类点
    alpha[ind] += eta  # 更新参数
    b += eta * y[ind]
    print('第{0}次迭代：alpha = {1}, b = {2}'.format(time, alpha, b))
    time += 1
    wrong = check()
# 计算超平面
w = np.dot(alpha, y * x)
print('感知机模型：w={0}, b={1}'.format(w, b))

迭代过程示例如下，有的时候因为选择点的问题可能还会出错，无法绘制，但是结果正确：

第1次迭代：alpha = [1. 0. 0.], b = [1]
第2次迭代：alpha = [1. 0. 1.], b = [0]
第3次迭代：alpha = [1. 0. 2.], b = [-1]
第4次迭代：alpha = [1. 0. 3.], b = [-2]
第5次迭代：alpha = [1. 1. 3.], b = [-1]
第6次迭代：alpha = [1. 1. 4.], b = [-2]
第7次迭代：alpha = [1. 1. 5.], b = [-3]
第8次迭代：alpha = [1. 1. 6.], b = [-4]
第9次迭代：alpha = [2. 1. 6.], b = [-3]
第10次迭代：alpha = [2. 1. 7.], b = [-4]
第11次迭代：alpha = [2. 1. 8.], b = [-5]
感知机模型：w=[2. 1.], b=[-5]

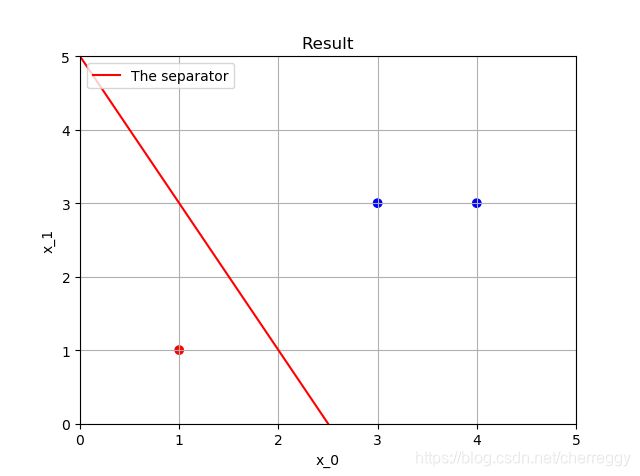
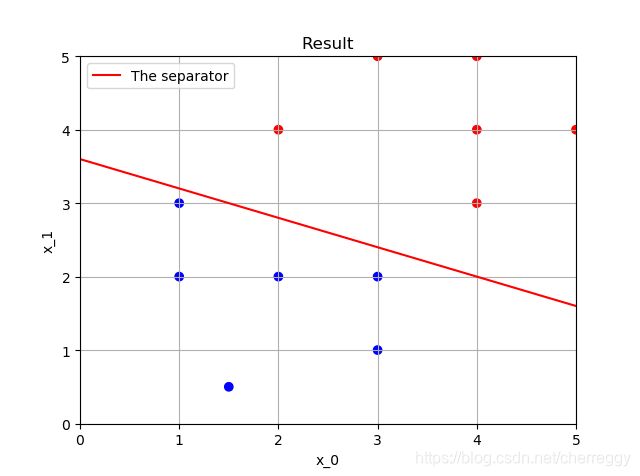
结果图绘制与之前相同：

# 绘制结果
plt.xlim((0, 5))  # 设置x坐标轴范围
plt.ylim((0, 5))  # 设置y坐标轴范围
map_color = {
     -1: 'r', 1: 'b'}  # 类别及其对应点颜色的映射
color = []
for dot in y:
    color += map_color[dot[0]]
plt.scatter(x[:, 0], x[:, 1], c=color)
x_p = np.linspace(0, 5, 100)
y_p = - b / w[1] - (w[0] / w[1]) * x_p
plt.plot(x_p, y_p, '-r', label='The separator')
plt.title('Result')
plt.xlabel('x_0')
plt.ylabel('x_1')
plt.legend(loc='upper left')
plt.grid()
plt.show()

其他数据点结果展示：