独家思维导图！让你秒懂李宏毅2020机器学习（二）—— Classification分类

独家思维导图！让你秒懂李宏毅2020机器学习（二）—— Classification分类

在上一篇文章我总结了李老师Introduction和regression的具体内容，即1-4课的内容，这篇我将会总结classification的内容（包括Generative Model和Discriminative Model）,即5-6课的内容（第6课Logistic Regression虽然名字叫regression实际上也是classification的内容），这两课的内容有点难懂，博主花了好长时间才理出头绪，当然，说的有不准确的地方还请各位大佬批评指正！

上一篇文章传送门独家思维导图！让你秒懂李宏毅2020机器学习（一）—— Regression回归

Classification

概念描述

分类（classification），即找一个函数判断输入数据所属的类别，可以是二类别问题（是/不是），也可以是多类别问题（在多个类别中判断输入数据具体属于哪一个类别）。与回归问题（regression）相比，分类问题的输出不再是连续值，而是离散值，用来指定其属于哪个类别。分类问题在现实中应用非常广泛，比如垃圾邮件识别，手写数字识别，人脸识别，语音识别等。

简单来说就是找一个function，它的input是一个object，它的输出是这个object属于哪一个class

特征数值化

上面说到classification的input是一个object，但object怎么输入呢？
我们需要用数字来表示这个object的特征，李老师宝可梦的例子是
用⽣命值(HP)、攻击⼒(Attack)、防御⼒(Defense)、特殊攻击⼒(Special Attack)、特殊防御⼒(Special defend)、速度(Speed)七种特性的数值所组成的vector来描述一只皮卡丘。

How to classification

好了，解决了input的问题，就需要找分类的方法了，一个直观的想法就是看能不能套用前面回归的做法。

Why not apply Regression?

总结一下，就是：
1.Regression的output是连续性质的数值，⽽classification要求的output是离散性质的点，我们很难找到⼀个Regression的function使⼤部分样本点的output都集中在某⼏个离散的点附近。
2. 线性回归用来解决分类问题时，稳定性差。当样本分布比较复杂时，线性回归无法做到准确的分类。

过于抽象？用李老师的例子来解释一下：
以binary classification为例，我们在Training时让输⼊为class 1的输出为1，输⼊为class 2的输出为-1；那么在testing的时候，regression的output是⼀个数值，它接近1则说明它是class 1，它接近-1则说明它是class 2

假设现在我们的model是 y=b+w1x1+w2x2，input是两个feature(x1,x2)
有两个class，蓝⾊的是class 1，红⾊的是class 2，
我们希望
蓝⾊的属于class 1的宝可梦，input到Regression的model，output越接近1越好；
红⾊的属于class 2的宝可梦，input到Regression的model，output越接近-1越好。
假设我们真的找到了这个function，如图所⽰，绿⾊的线表⽰b+w1x1+w2x2=0，也就是class 1和class 2的分界线，这种情况下，值接近-1的宝可梦都集中在绿线的左上⽅，值接近1的宝可梦都集中在绿线的右下⽅，这是合理的。

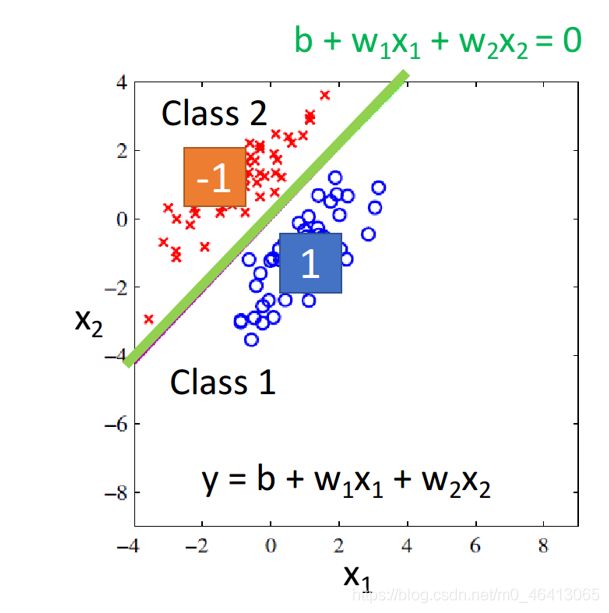
但是上述现象只会出现在样本点⽐较集中地分布在output为-1和1的情况，如果像下图所⽰，显然绿线为最好的那个model的分界线
但如果将所有样本点通过Regression训练出来的model，会是紫⾊这条分界线对应的model
因为相对于绿线，它“减⼩”了由右下⻆这些点所带来的error，也就是说，regression会考虑相距分界线较远的点

也就是说，
Regression对样本分布太敏感了
假如现在负样本比较多，那么回归线将会更靠近负样本，使得正样本的预测值下降。
为了使损失函数（均方差）最小化，回归线要朝着负样本的方向移动；
即上面的的function会为了使损失函数（均方差）最小化，由绿线的位置向右下角距离较远的蓝色样本点偏移，变成紫色部分。

所以，Regression定义model好坏的定义⽅式对classification来说是不适⽤的
再简单点说，两点pass掉了regression：
1.线性回归的预测值是连续值的形式，不是概率的形式
2.对数据分布比较敏感

好的，接下来我们终于可以进入正题了！
Wait！还需要一点概率论的前置知识，当然，熟练掌握概率论的大佬请跳过

Prepositional knowledge

Generative model

终于步入正题了！

Binary Classification

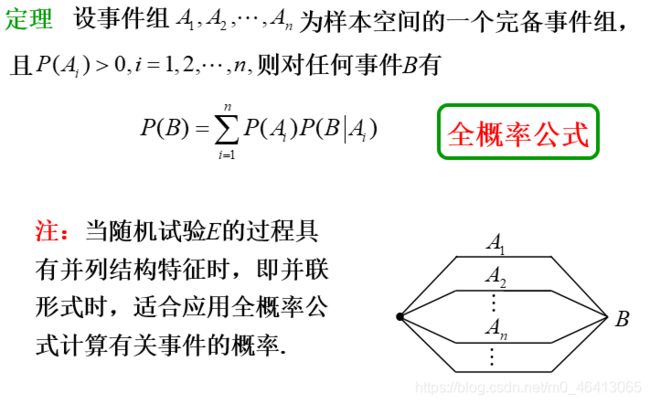
首先考虑⼆元分类的问题，我们拿到⼀个input x，想要知道这个x来自于class 1或class 2的概率
这不就是我上文讲的贝叶斯公式嘛！

由图我们可以得到以下两个公式


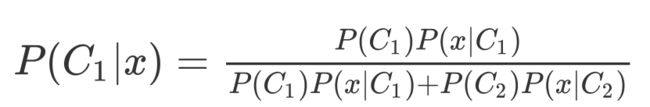
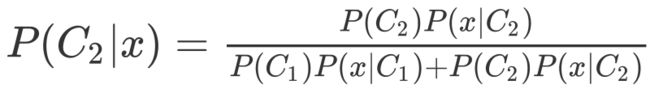
先提一点，在这里P(C1|x)+P(C2|x)=1哟，也就是说，我们只需求一即可。
当P(C1|x)>0.5 我们就说x是属于C1的

其中P(C1),P(C2)这两个值还是比较好求的
在Training data⾥⾯，有79只⽔系，61只⼀般系
P(C1)=79/(79+61)=0.56
P(C2)=61/(79+61)=0.44

关键在于如何得到P(x|C1)和P(x|C2)

错误的想法：
假设我们的x是⼀只新来的海⻳，但是在我们79只⽔系的宝可梦training data⾥⾯根本就没有海⻳，所以挑⼀只海⻳出来的可能性根本就是0啊！

实际上，这这已有的79只⽔系宝可梦的data其实只是冰⼭⼀⻆，这些只是从一个概率密度函数中挑出来的样本，设这个概率密度函数为f(x),则
P(x|C1)=f(x)

在这里，李老师设这个概率密度函数为Gaussian,我们要通过这79个已知的样本点来找出生成这些样本点可能性最大的Gaussian,即由冰山一角推算整个冰山。

很自然的想到用极大似然估计法来估测这个Gaussian（实际上就是求μ和Σ）做法是
找出最特殊的那对μ和Σ，从它们共同决定的⾼斯函数中再次采样出79个点，使”得到的分布情况与当前已知79点的分布情况相同“这件事情发⽣的可能性最⼤

假设这79个样本独立同分布（极大似然法条件）可得到李老师如下极大似然函数

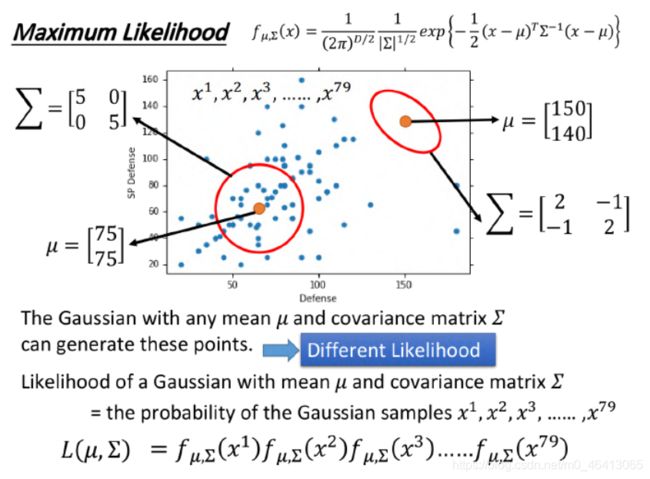
极大似然函数
实际上就是该事件发⽣的概率就等于每 个点都发⽣的概率之积，我们只需要把79个点中每⼀个点的data代进去，就可以得到⼀个关于μ和Σ的函数，分别求偏导，解出微分是0的点，即使L最⼤的那组参数，便是最终的估测值，通过微分得到的⾼斯函数的 μ和Σ的最优解如下：

即μ刚好是数学期望，Σ刚好是协⽅差（这个可以当作公式来记忆）

李老师最终算的值如下：

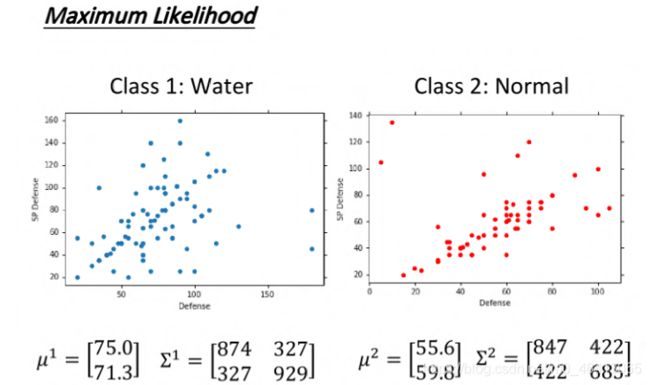
然后其实就可以算概率进行分类了
当P(C1|x)>0.5 —— x->C1
当P(C1|x)<0.5 —— x->C2

老师把testing data上得到的结果可视化出来

注意，划重点，由刚刚两个样本分别求出来的自己的μ和Σ得到的boundary是曲线
同时，这个准确率也不好

Why？

->还记得之前的两个Error吗？
其实variance是跟input的feature size的平⽅成正⽐的，所以当feature的数量很⼤的时候，Σ⼤⼩的增⻓是可以⾮常快的，在这种情况下，给不同的Gaussian以不同的Σ（covariance matrix），会造成model的参数太多，⽽参数多会导致该model的variance过⼤，出现overfitting的现象，因此对不同的class使⽤同⼀个Σ（covariance matrix），可以有效减少参数

于是，常见的做法是：不同的 class可以share同⼀个Σ(covariance matrix),注意不同class自己的概率密度函数的μ还是不同的

此时就把μ1、μ2和共同的Σ⼀起去合成⼀个极⼤似然函数，此时可以发现，得到的 μ1、μ2和原来⼀样，还是各⾃的均值，⽽Σ则是原先两个Σ1和Σ2的加权

然后像上面那样对结果进行可视化：

惊讶的发现，不仅共用后正确率提高了而且：
没有共⽤covariance matrix——分界线：⼀条曲线；
如果共⽤covariance matrix——分界线：⼀条直线；

奇怪，这直线怎么解释呢？
我们可以把原来要求的概率形式化简一下：
表达式上下同除以分⼦，有没有觉得形式很像一个常用函数（划重点）

sigmoid function(S函数)，我们把该式设成这个函数

引入参数z，再反解z，再化简z

可以看出，当Σ1和Σ2不相等时z是一大堆复杂的式子时：
boundary(分界线)为P(x|C1)=0.5的那条线，即z=0的那条线
此时z=0显然为曲线。

但当Σ1和Σ2相等时

此时分界线z=0为一条直线。

以上就是Generative Model的分类方法，可以看出，这个方法我们先有一个预设的概率密度函数模型，然后再用极大似然法来寻找预设概率密度函数模型的参数，求出我们基于贝叶斯公式的那个概率来判断分类，那能不能我们不预设概率密度函数模型呢？能不能我们不算，自动把那个概率密度函数找出来呢？于是我们就有了分类的第二个处理手段Logistic Regression

Logistic Regression（Discriminative）

还记得上节在Gaussian的distribution下考虑class 1和class 2共⽤Σ，可以得到⼀个线性的z吗？
其实很多其他的Probability model经过化简以后也都可以得到同样的结果，这节我们就基于z为线性来展开

即用上面的贝叶斯模型，可以将求P(C1|x)的问题转化为求sigmoid(z)的问题，即转换为求z的问题，也就是求线性z函数的w和b，于是我们节的任务说白了就是找w和b

还记得我上篇提到的机器学习的三个步骤吗？
Step 1： Function set
Step 2： Goodness of a function
Step 3： Find the best function

Step 1： Function set

这⾥的function set就是Logistic Regression——逻辑回归

Step 2： Goodness of a function

像刚刚一样，我们还是要找一个最有可能生成我们这些样本点的概率密度函数概率密度函数
但这次，我们不做预设，只是简简单单的把它看作f(x)=sigmoid(z)=P(C1|x)
于是我们表示出生成这些样本点的概率（就是极大似然估计函数）

并作如下化简：


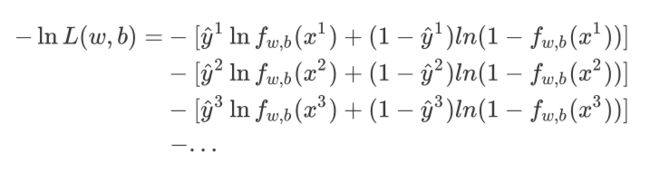
(由于class 1和class 2的概率表达式不统⼀，上⾯的式⼦⽆法写成统⼀的形式，为了统⼀格式，这⾥将Logistic Regression⾥的所有Training data都打上0和1的标签，即output y^=1 代表class 1，output y=2 代表class 2)

即我们要找的参数实际上就是：

这⾥xn表⽰第n个样本点，yn表⽰第n个样本点的class标签(1表⽰class 1,0表⽰class 2)，最终这个summation的形式，⾥⾯其实是两个Bernouli distribution(两点分布)的cross entropy(交叉熵)
交叉熵实际上表达的是希望这个function的output和它的target越接近越好

不过这个argmin你们有没有觉得眼熟呢？
还记得上文的Loss函数吗，博主感觉，这里的交叉熵就可以看作Loss函数

Step 3： Find the best function

那既然可以看作Loss函数，Find the best function的方法就直接照搬了——gradient descent

还记得上一篇的gradient descent吗？回顾一下：

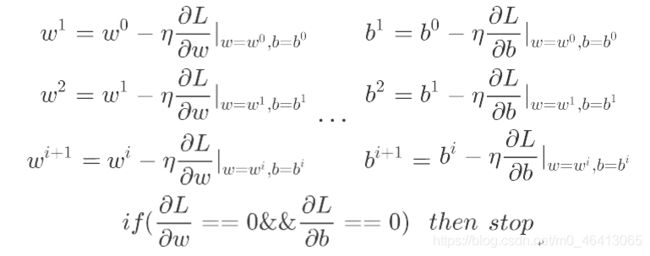
因此，我们要求偏导了
Tip:sigmoid function的微分:

得到最终的结果：

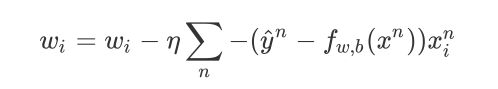
首先分析下，原来update取决于三件事：

• ⾃⼰设定的 learning rate
• 来⾃于data的 xi
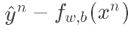• 代表function的output跟理想target的差距有多⼤，如果离⽬标越远，update的步伐就要越⼤

其次，有没有发现这个式子有点眼熟？
我们直接放出Logistic Regression与Linear Regression的对比图

Logistic Regression VS Linear Regression

Logistic Regression和linear Regression的 update的⽅式是⼀模⼀样的！
唯⼀不⼀样的是，Logistic Regression的target 和output 都必须是在0和1之间的，
⽽linear Regression的target和output的范围可以是任意值。

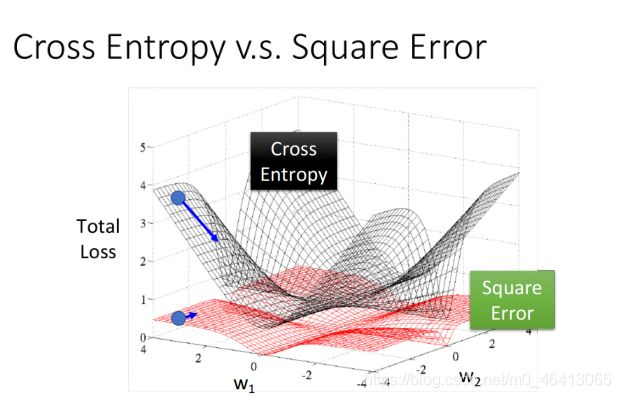
还有一点值得我们注意的是，为什么Logistic Regression的Loss function不用Square error而用交叉熵呢？

Why not apply Square error?

那我们就用Square error来当Loss函数试一下呗！

通过计算可以发现用Square Error在far from target的地方，梯度也接近于0，这样就会使Loss fuction一直Stuck停滞不前,具体可以可视化如下图：

Multi-class Classification

上面无论是Generative model还是Discriminative model都是拿Binary Classification举例的，对于多元的，其实流程是一样的，不过有两个小的改变

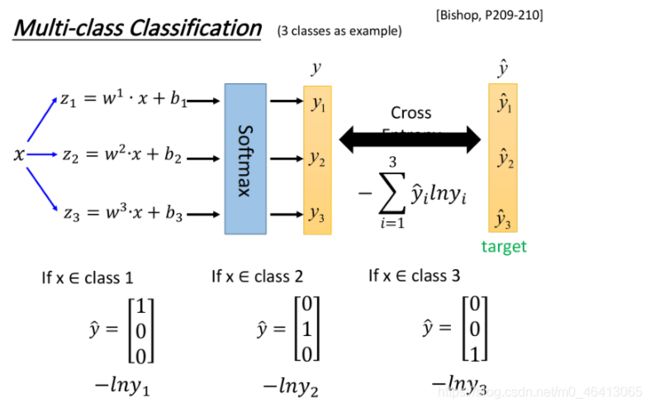
上面二元的是采用sigmoid来分类的，三元我们采用softmax来分类：

我们把 丢进⼀个softmax的function，softmax做的事情是这样三步：

1. 取exponential，得到e^z1,e^z2, e^z3
2. 把三个exponential累计求和，得到totalsum=Σe^zi
3. 将total sum分别除去这三项(归⼀化)，得到 y1,y2,y3
   
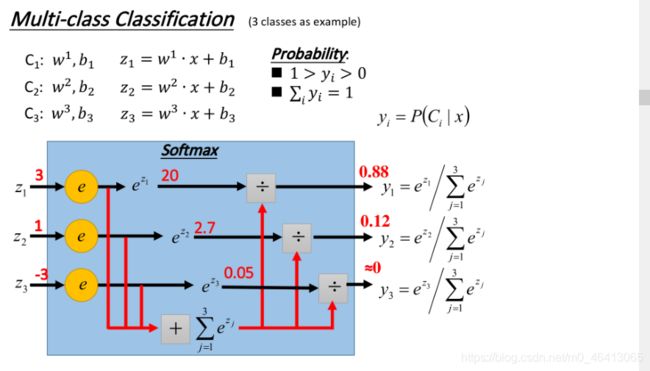
   原来的output z可以是任何值，但是做完softmax之后，你的output的值⼀定是介于0~1之间，并且它们的和⼀定是1

假设我们⽤的是Gaussian distribution(共⽤covariance)，经过⼀般推导以后可以得到softmax的function，⽽从information theory也可以推导出softmax function，Maximum entropy本质内容和Logistic Regression是⼀样的，这就跟二元是用sigmoid同理。

第二个改变是
我们在训练的时候还需要有⼀个target，因为是三个class， output是三维的，对应的target也是三维的，为了满⾜交叉熵的条件，target 也必须是probability distribution，这⾥我们不能使⽤1,2,3作为class的区分，为了保证所有class之间的关系是⼀样的，这⾥使⽤类似于one-hot编码的⽅式，即

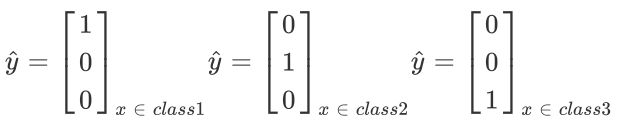
然后接下来就是一样的流程，我就不做过多赘述了

这一章最后还有个有趣的东西，即由Limitation of Logistic Regression引出了Deep Learning

Limitation of Logistic Regression

李老师举了个例子来说明这个limitation

这个例子中，我们无法通过一条直线来分割Class1和Class2

但是，如果变化一下feature space，就能重新分个，例如
假设这⾥定义
x1’是原来的点到(0,0)之间的距离，x2’是原来的点到(1,1) 之间的距离，重新映射之后如下
图右侧(红⾊两个点重合)，此时Logistic Regression就可以把它们划分开来

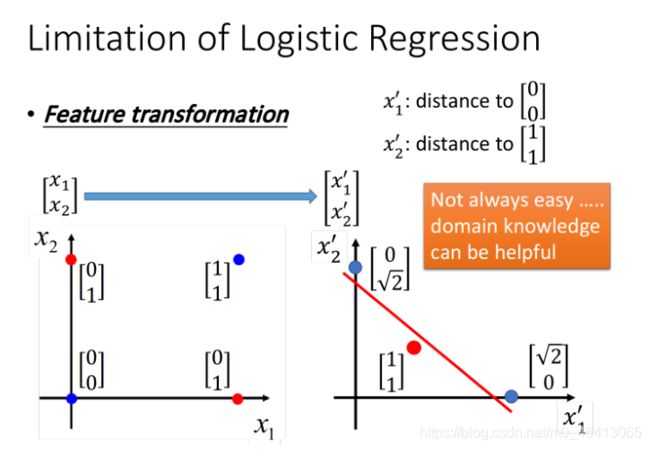
然而，我们人工找这样的变换是十分困难的，我们需要用机器来找

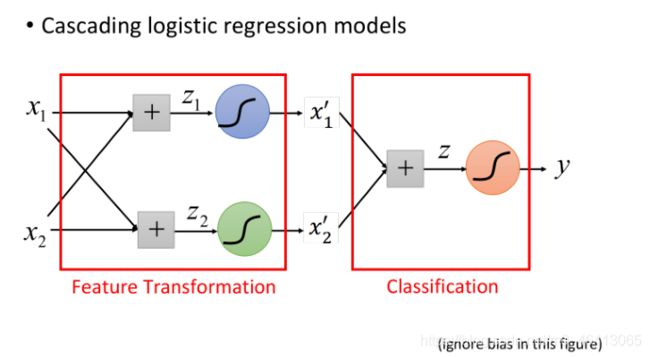
因此着整个流程是，先⽤n个Logistic Regression做feature Transformation(n为每个样本点的feature数量)，⽣成n个新的feature，然后再⽤⼀个Logistic Regression作classifier
Logistic Regression的boundary⼀定是⼀条直线，它可以有任何的画法，但肯定是按照某个⽅向从⾼ 到低的等⾼线分布，具体的分布是由Logistic Regression的参数决定的，每⼀条直线都是由z=b+Σwⁱxⁱ组成的(⼆维feature的直线画在⼆维平⾯上，多维feature的直线则是画在多维空间上)
下图是⼆维feature的例⼦，分别表⽰四个点经过transform之后的x1’和x2’ ，在新的feature space中可以通过最后的Logistic Regression划分开来

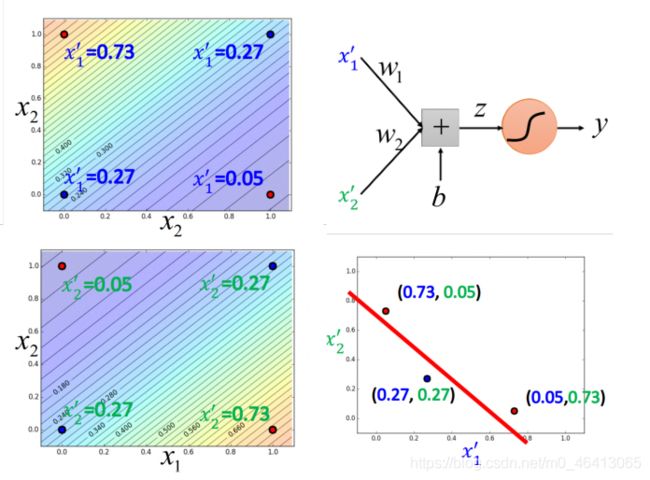
Powerful Cascading Logistic Regression

通过上⾯的例⼦，我们发现，多个Logistic Regression连接起来会产⽣powerful的效果，我们把每⼀个
Logistic Regression叫做⼀个neuron(神经元)，把这些Logistic Regression串起来所形成的network，就叫做Neural Network，就是类神经⽹路，这个东西就是Deep Learning！