Merging Pose Estimates Across Space and Time论文解析
Merging Pose Estimates Across Space and Time论文解析
- 简介
-
- 1 引言
-
- 1.1相关工作
- 2 提出方法
-
- 2.1单帧
- 2.2多帧
- 2.2变量K
- 3.结果
-
- 3.1 Buffy stickmen数据集
-
- 3.1.1 Original Buffy 数据集没有时间信息
- 3.1.2 Video Buffy数据集
- 3.2 Faces
- 3.3 Mice
- 4.总结
简介
Merging Pose Estimates Across Space and Time字面意思:在空间和时间上合并姿态估计,文章的主要贡献是提出了Pose-NMS框架,基本思想是通过聚类得到最终姿态,下面将按照论文的顺序进行详细介绍。(注:本文只供学习讨论,不做商业用途,建议大家去官网下载原文阅读,本文观点只是个人学习中的感悟,如果您有更好的想法或者发现错误请私信我交流,或在评论区分享您的观点)

合并目标检测框采用多种NMS作为目标检测的后处理方案,我们提出了一种NMS的泛化方法,可以在单帧中合并多个姿态估计,在 standard NMS中最后的估计不是medoids而是centroids,因此比任何单独的候选区都精确,采用相同的数学框架,我们将我们的方法扩展到多帧设置,合并跨空间和时间的多个独立姿势估计,并输出场景中对象的数量和姿势。我们的方法避开了与完全跟踪相关的许多固有挑战(例如,物体进入/离开场景、长时间遮挡等)。为了证明方法的通用性,我们将其应用于人体、人脸和小鼠三个领域的两种最新姿态估计算法,我们的方法提高了检测精度(通过消除相似)和姿态估计质量,并且计算效率高
- 思想来源:目标检测中的 NMS ;
- 创新: standard NMS ,最后估计出的是centroids,精确度提高,可以跨空间和时间合并,输出场景中对象的数量和姿势;
- 不足:避开了许多固有挑战物体进入/离开场景、长时间遮挡 等;
- 优点:通用性强,检测更精确,提高了姿态估计质量,计算效率高 功能;
1 引言
精确的视频姿态估计是动作识别【6,23】、运动捕捉【20】、与人机交互【21】等应用的关键。这里的姿势是指模型的参数,它描述了图像中物体的结构,或图像中物体的坐标位置。
数据驱动的姿态估计方法越来越成熟,在许多识别任务中取得了令人惊叹的效果【7, 13, 25, 26】,这些方法输出一组姿势估计,通过“非极大值抑制”(NMS)技术来合并相似目标检测。NMS是可以有效合并目标检测产生的多余边界框【9,11】,然而,目前还不能将其应用到姿态估计。如【25,26】中所述,只是将标准NMS单独应用于每个关节位置,效果并不理想。
大意:NMS不能直接用于姿估计


第一个贡献:提出在单帧中合并多姿态估计的框架。是目标检测NMS的衍生物。该框架适用于大部分姿态估计方法而且可以提高精度,比较通用。通过鲁棒平均来实现,解决多目标姿态估计之间的对应问题。
第二个贡献:用相同的数学框架把我们的方法应用到多帧连续检测,进一步提高姿态估计。该方法受到了“‘tracking by detection”方法的启发,但回避了许多固有挑战(例如,物体进入或离开场景,长时间的遮挡等)。我们的方法可以跨空间和时间合并多姿态估计,输出场景中对象的数量和姿态,参见图1。
大意:本文两个贡献,第一:单帧合并姿态的框架。第二:多帧合并姿态
 利用统一的优化框架,我们得到了一个高效的方法,可以有效估计短视频(每帧具有相同对象且连续)的姿态。Pose-NMS不依赖选取的姿态估计方法,任何逐帧的姿态估计方法都可以使用Pose-NMS。
利用统一的优化框架,我们得到了一个高效的方法,可以有效估计短视频(每帧具有相同对象且连续)的姿态。Pose-NMS不依赖选取的姿态估计方法,任何逐帧的姿态估计方法都可以使用Pose-NMS。
我们将姿势NMS应用于两种不同的最新姿势估计方法来展示姿势NMS的普适性:DPM[25]和CPR[7,13]。我们从包含三种不同对象类型的场景中收集了1000多个视频短片,用三个任务检测我们的方法。三个任务:人体姿态估计,人脸定位估计和动物姿态估计。与标准技术相比,Pose-NMS在三种情况下都提高了检测精度和姿态估计质量。我们的方法代码可以在线上获得。
大意:将Pose-NMS应用于DPM和CPR姿态检测,利用人体姿态估计,人脸定位估计和动物姿态估计验证Pose-NMS的效果,简单说就是想让你知道Pose-NMS为啥牛逼。
1.1相关工作
 之前的视频估计可以划分为两大类:(1) 将跟踪和姿态估计直接耦合在一起。 (2)先逐帧估计姿态和随后在帧之间执行时间平滑。
之前的视频估计可以划分为两大类:(1) 将跟踪和姿态估计直接耦合在一起。 (2)先逐帧估计姿态和随后在帧之间执行时间平滑。

第一类方法,主要用于无标记人体运动捕捉和多个摄像机的三维姿态估计[20]。例入参考文献[22]通过a factored-state Hierarchical HMM同时执行跟踪和姿势估计,或[18]通过Viterbi-style maximum likelihood方法结合运动模型和观察对象,来集成单帧姿势恢复和时间积分的方法。这些方法不易推广到其他姿态估计任务。
第二类方法,使用于单目视频的标准二维姿态估计,通过加强帧间的时间连续性,将单帧图像检测方法扩展到视频。通过单帧检测计算出在一段时间内连续的物体轨迹[1,2,3,5,8]。检测跟踪是一种非常有效的跟踪方法,但无法扩展到姿态参数化。
大意:两类方法都有缺陷
2 提出方法
 现在详细描述我们的方法,给定一个包含T帧的视频,将姿态检测应用于从第一帧到第T帧的每一帧,并返回姿态估计 X t = { x 1 t , . . . , x n t t ∣ x i t ∈ R D } \Chi^t=\{x_1^t,...,x_{n^t}^t|x_i^t \in\R^D\} Xt={ x1t,...,xntt∣xit∈RD}和相应的置信度 S t = { s 1 t , . . . , s n t t ∣ s i t ∈ R D } S^t=\{s_1^t,...,s_{n^t}^t|s_i^t \in\R^D\} St={ s1t,...,sntt∣sit∈RD}, n t n^t nt是在第t帧估计出的目标数, x i t x_i^t xit用D维参数化,D维度因任务而异,可能包括角度值。我们的目标是计算出每一帧中原始姿态的轨迹 Y t = { y 1 t , . . . , y K t ∣ y k t ∈ R D } Y^t=\{y_1^t,...,y_K^t|y_k^t \in\R^D\} Yt={ y1t,...,yKt∣ykt∈RD},并且进行时间平滑,K是需要估计的对象数。
现在详细描述我们的方法,给定一个包含T帧的视频,将姿态检测应用于从第一帧到第T帧的每一帧,并返回姿态估计 X t = { x 1 t , . . . , x n t t ∣ x i t ∈ R D } \Chi^t=\{x_1^t,...,x_{n^t}^t|x_i^t \in\R^D\} Xt={ x1t,...,xntt∣xit∈RD}和相应的置信度 S t = { s 1 t , . . . , s n t t ∣ s i t ∈ R D } S^t=\{s_1^t,...,s_{n^t}^t|s_i^t \in\R^D\} St={ s1t,...,sntt∣sit∈RD}, n t n^t nt是在第t帧估计出的目标数, x i t x_i^t xit用D维参数化,D维度因任务而异,可能包括角度值。我们的目标是计算出每一帧中原始姿态的轨迹 Y t = { y 1 t , . . . , y K t ∣ y k t ∈ R D } Y^t=\{y_1^t,...,y_K^t|y_k^t \in\R^D\} Yt={ y1t,...,yKt∣ykt∈RD},并且进行时间平滑,K是需要估计的对象数。
大意:介绍各个参数的含义 X t \Chi^t Xt就是t帧画面中经过目标检测出的边界框,同一个目标会有许多边界框, n t n^t nt是边界框的总数, S t S^t St是每个边界框的置信度,置信度越高的框越准确, Y t Y^t Yt是画面中每个对象的最后姿态。
2.1单帧
 我们开始讨论如何合并t帧内的多个姿态,假设目标总数K是已知的,该方法的核心是将问题看作原始姿态的鲁棒聚类,对每个物体的姿态进行更精确的估计。
我们开始讨论如何合并t帧内的多个姿态,假设目标总数K是已知的,该方法的核心是将问题看作原始姿态的鲁棒聚类,对每个物体的姿态进行更精确的估计。
设d(x,y)=||x-y|| 2 2 _2^2 22为欧氏距离的平方。在t帧中给定 X t \Chi^t Xt和 S t S^t St,定义 Y t Y^t Yt的损失函数为:
L s p a c e ( Y t ) = 1 S t ∑ i = 1 n t min k d ( x i t , y k t ) s i t L_{space}(Y^t)=\frac{1}{S^t}\displaystyle\sum_{i=1}^{n^t}\min\limits_kd(x_i^t,y_k^t)s_i^t Lspace(Yt)=St1i=1∑ntkmind(xit,ykt)sit, w h e r e S t = ∑ i = 1 n t s i t \quad where S^t=\displaystyle\sum_{i=1}^{n^t}s_i^t whereSt=i=1∑ntsit
大意:提出损失函数 L s p a c e L_{space} Lspace
 L s p a c e L_{space} Lspace使 y k t 接 近 x i t y_k^t接近x_i^t ykt接近xit,损失函数 L s p a c e L_{space} Lspace的缺点是: y k t y_k^t ykt可以体现相距较远的姿态 x i t x_i^t xit(换句话说,相距较远的 x i t x_i^t xit会影响 y k t y_k^t ykt), y k t y_k^t ykt应该体现与目标相近的大部分检测结果,而不是相距较远的某几个姿态,通过定义有界距离度量我们将损失函数优化为 d b d ( x , y ) = m i n ( z , ∣ ∣ x − y ∣ ∣ 2 2 ) d_{bd}(x,y)=min(z,||x-y||_2^2) dbd(x,y)=min(z,∣∣x−y∣∣22), d b d d_{bd} dbd是平方欧氏距离的变形,不同点是它有最大值z,最后损失函数为:
L s p a c e L_{space} Lspace使 y k t 接 近 x i t y_k^t接近x_i^t ykt接近xit,损失函数 L s p a c e L_{space} Lspace的缺点是: y k t y_k^t ykt可以体现相距较远的姿态 x i t x_i^t xit(换句话说,相距较远的 x i t x_i^t xit会影响 y k t y_k^t ykt), y k t y_k^t ykt应该体现与目标相近的大部分检测结果,而不是相距较远的某几个姿态,通过定义有界距离度量我们将损失函数优化为 d b d ( x , y ) = m i n ( z , ∣ ∣ x − y ∣ ∣ 2 2 ) d_{bd}(x,y)=min(z,||x-y||_2^2) dbd(x,y)=min(z,∣∣x−y∣∣22), d b d d_{bd} dbd是平方欧氏距离的变形,不同点是它有最大值z,最后损失函数为:
L s p a c e ( Y t ) = 1 S t ∑ i = 1 n t min k d b d ( x i t , y k t ) s i t L_{space}(Y^t)=\frac{1}{S^t}\displaystyle\sum_{i=1}^{n^t}\min\limits_kd_{bd}(x_i^t,y_k^t)s_i^t Lspace(Yt)=St1i=1∑ntkmindbd(xit,ykt)sit
这个函数跟上面的很像,唯一的不同在于是 d d b d_{db} ddb不是d,现在,一旦 x i t x_i^t xit离 y t y^t yt特别远,它只会得到最大惩罚z而不会影响 y k t y_k^t ykt,常数z取决于实际应用。实际上我们总是将z设为以像素为单位的对象平均宽度。
大意:欧式距离的平方d的缺点是会考虑一些细枝末节的东西,就像是修剪树枝,只需要留下来主干,剪掉细枝末节不影响树的形状,但是留下它们会影响模型树干的泛化能力,也就是来年春天的树还是只能和今年一摸一样,限制了树的发展,所以为了更好的提取树干姿态,提出了 d d b d_{db} ddb,它把树干的范围限制在z内,不考虑超出z的细枝末节。

我们现在直观的感受一下 L s p a c e L_{space} Lspace的优化过程,我们首先看式(1)中损失,这是当k=K并且 Y t Y^t Yt为中心时(加权)k-均值聚类的损失。如果K已知,可以用加权k-均值为第t帧提供合理的解决方案,但是如果用 d d b d_{db} ddb代替d,k-均值就不再适用了。
我们为式(2)定义了一个k-均值的简单变形——有界k-均值,为了下面的讨论,我们去掉了上标。在k-means算法的每个阶段,首先确定类的成员关系,然后将每个类中心设置为该类的点的平均值。在标准k-均值中,如果 d ( x i , y k ) < d ( x i , y j ) , ∀ j ≠ k d(x_i,y_k)
大意:提出了有界k-均值,目的是为了优化损失,我的直观理解是,它的核心思想就是x离某个聚类y近,就把它归给该聚类y。
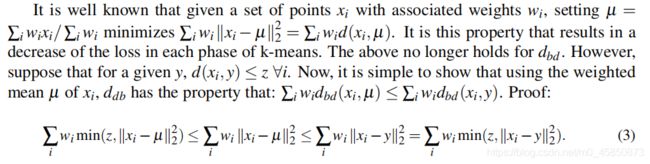
已知一组权重为 w i w_i wi的点 x i x_i xi,当 µ = ∑ i w i x i / ∑ i w i µ=\sum_iw_ix_i/\sum_iw_i µ=∑iwixi/∑iwi时 ∑ i w i ∣ ∣ x i − µ ∣ ∣ 2 2 = ∑ i w i d ( x i , µ ) \sum_iw_i||x_i-µ||_2^2=\sum_iw_id(x_i,µ) ∑iwi∣∣xi−µ∣∣22=∑iwid(xi,µ)取的最小值,减少了k-均值每个阶段的损失。但 d d b d_{db} ddb不能用这种方法优化,假设y,且 d ( x i , y ) ⩽ z , ∀ i d(x_i,y)\leqslant z,\forall i d(xi,y)⩽z,∀i,µ是 x i x_i xi的加权平均值,对于 d b d d_{bd} dbd有: ∑ i w i d d b ( x i , µ ) ⩽ ∑ i w i d d b ( x i , y ) \sum_iw_id_{db}(x_i,µ)\leqslant\sum_iw_id_{db}(x_i,y) ∑iwiddb(xi,µ)⩽∑iwiddb(xi,y),证明:
∑ i w i m i n ( z , ∣ ∣ x i − µ ∣ ∣ 2 2 ) ⩽ ∑ i w i ∣ ∣ x i − µ ∣ ∣ 2 2 ⩽ ∑ i w i ∣ ∣ x i − y ∣ ∣ 2 2 = ∑ i w i m i n ( z , ∣ ∣ x i − y ∣ ∣ 2 2 ) \sum_iw_imin(z,||x_i-µ||_2^2)\leqslant\sum_iw_i||x_i-µ||_2^2\leqslant\sum_iw_i||x_i-y||_2^2=\sum_iw_imin(z,||x_i-y||_2^2) ∑iwimin(z,∣∣xi−µ∣∣22)⩽∑iwi∣∣xi−µ∣∣22⩽∑iwi∣∣xi−y∣∣22=∑iwimin(z,∣∣xi−y∣∣22)
注意: ∑ i w i ∣ ∣ x i − y ∣ ∣ 2 2 = ∑ i w i m i n ( z , ∣ ∣ x i − y ∣ ∣ 2 2 ) \sum_iw_i||x_i-y||_2^2=\sum_iw_imin(z,||x_i-y||_2^2) ∑iwi∣∣xi−y∣∣22=∑iwimin(z,∣∣xi−y∣∣22)是相等的,因为y的取值限定在 d ( x i , y ) ⩽ z d(x_i,y)\leqslant z d(xi,y)⩽z
大意:欧式距离平方d有最优解,很容易就可以求解,但是它的变形 d d b d_{db} ddb不能按照这种方法求最优解,只能一步步优化,逐渐逼近最优解,可能会取到最优,但大部分情况都不能取到最优,这种情况可以选择不同的初始值,多次尝试逼近最优。
 也就是将y换成在z距离内 x i x_i xi的加权平均值µ,用这样的替换减小每个阶段的损失(或保持其恒定)。但是µ不是 ∑ i w i d d b ( x i , µ ) \sum_iw_id_{db}(x_i,µ) ∑iwiddb(xi,µ)的最小值;只是优于 d ( x i , y ) ⩽ z , ∀ i d(x_i,y)\leqslant z,\forall i d(xi,y)⩽z,∀i的任何y。因此,虽然有界k-均值在一步步减少损失,但不能保证是最优的(在标准k-均值算法中,虽然交替优化过程不是最优的,但每一步都是最优的),不同的初始化可以改善这个问题。
也就是将y换成在z距离内 x i x_i xi的加权平均值µ,用这样的替换减小每个阶段的损失(或保持其恒定)。但是µ不是 ∑ i w i d d b ( x i , µ ) \sum_iw_id_{db}(x_i,µ) ∑iwiddb(xi,µ)的最小值;只是优于 d ( x i , y ) ⩽ z , ∀ i d(x_i,y)\leqslant z,\forall i d(xi,y)⩽z,∀i的任何y。因此,虽然有界k-均值在一步步减少损失,但不能保证是最优的(在标准k-均值算法中,虽然交替优化过程不是最优的,但每一步都是最优的),不同的初始化可以改善这个问题。
如果姿态包含角度,则距离函数和优化过程需要修改,有关详细信息,请参阅补充资料。
大意:使用不同初始化,争取逼近到最优解。以上的优化没有考虑角度信息。
2.2多帧
 在视频中,需要保证跨帧的姿态预测是一致的。为了将上面讨论的方法扩展到多个帧,我们在损失中添加了第二项,使相同对象 y k t y_k^t ykt的预测在相邻帧之间保持紧密
在视频中,需要保证跨帧的姿态预测是一致的。为了将上面讨论的方法扩展到多个帧,我们在损失中添加了第二项,使相同对象 y k t y_k^t ykt的预测在相邻帧之间保持紧密
L t i m e ( Y t − 1 , Y t ) = 1 K ∑ k = 1 K d ( y k t − 1 , y k t ) , L_{time}(Y^{t-1},Y^t)=\frac{1}{K}\displaystyle\sum_{k=1}^{K}d(y_k^{t-1},y_k^t), Ltime(Yt−1,Yt)=K1k=1∑Kd(ykt−1,ykt),
d是欧氏距离的平方。总的来说,损失:
L ( Y ) = ∑ t = 1 T L s p a c e ( Y t ) + λ ∑ t = 2 T L t i m e ( Y t − 1 , Y t ) L(Y)=\displaystyle\sum_{t=1}^{T}L_{space}(Y^t)+\lambda\displaystyle\sum_{t=2}^{T}L_{time}(Y^{t-1},Y^t) L(Y)=t=1∑TLspace(Yt)+λt=2∑TLtime(Yt−1,Yt)
λ是自己设定的,控制时间项在损失中所占的比例。λ=1说明空间项和时间项的重要性相等。
大意:之前都是单帧,所以只用考虑空间信息,多帧则需要考虑时间信息, L t i m e L_{time} Ltime的意思是要使相邻两帧的姿态y紧密相邻(原因也很简单,相邻帧的同一个对象不可能出现较大的移动),这里有一个 λ \lambda λ,控制时间项的比例,如果你想让视频中的姿态流畅,就增加 λ \lambda λ就对了
 现在看一下公式(5)的优化过程,给定初始Y,在t帧迭代细化Y,损失 L ( Y ) L(Y) L(Y)将减小。假设1
现在看一下公式(5)的优化过程,给定初始Y,在t帧迭代细化Y,损失 L ( Y ) L(Y) L(Y)将减小。假设1
L ( Y t ) = 1 S t ∑ i = 1 n t min k d b d ( x i t , y k t ) s i t + λ 1 K ∑ k = 1 K ( d ( y k t , y k t − 1 ) + d ( y k t , y k t + 1 ) ) L(Y^t)=\frac{1}{S^t}\displaystyle\sum_{i=1}^{n^t}\min\limits_kd_{bd}(x_i^t,y_k^t)s_i^t+\lambda\frac{1}{K}\displaystyle\sum_{k=1}^{K}(d(y_k^{t},y_k^{t-1})+d(y_k^{t},y_k^{t+1})) L(Yt)=St1i=1∑ntkmindbd(xit,ykt)sit+λK1k=1∑K(d(ykt,ykt−1)+d(ykt,ykt+1))
用 a i k t a_{ik}^t aikt替换 min k \min\limits_k kmin,用 d b d d_{bd} dbd替换d:
L ′ ( Y t ) = S − t S t z + 1 S t ∑ i = 1 n t a i k t d b d ( x i t , y k t ) s i t + λ 1 K ∑ k = 1 K ( d ( y k t , y k t − 1 ) + d ( y k t , y k t + 1 ) ) L'(Y^t)=\frac{\stackrel{-t}{S}}{S^t}z+\frac{1}{S^t}\displaystyle\sum_{i=1}^{n^t}a_{ik}^td_{bd}(x_i^t,y_k^t)s_i^t+\lambda\frac{1}{K}\displaystyle\sum_{k=1}^{K}(d(y_k^{t},y_k^{t-1})+d(y_k^{t},y_k^{t+1})) L′(Yt)=StS−tz+St1i=1∑ntaiktdbd(xit,ykt)sit+λK1k=1∑K(d(ykt,ykt−1)+d(ykt,ykt+1))
w h e r e a i k t = 1 [ d ( x i t , y k t ) ⩽ d ( x i t , y j t ) ∀ j a n d d ( x i t , y k t ) < z ] where\quad a_{ik}^t=1[d(x_i^t,y_k^t)\leqslant d(x_i^t,y_j^t)\forall j \quad and\quad d(x_i^t,y_k^t)
大意:这些公式就变形,仔细看看前面的公式,无非就是替换,或者换一个定义,where条件中的1翻译的是指标函数,我也不太清楚,不过我之前看的论文里面提到过,如果[ ]里面的内容成立,那这个1指标函数的值就是1,我的理解就是,把x限制在一个范围内,就可以用欧氏距离的平方d代替 d d b d_{db} ddb,目的就是好计算嘛,因为 d d b d_{db} ddb这里面有非线性的min,不好逆推呀。
 其中1为指标函数, s − t \stackrel{-t}{s} s−t为未分配到任何聚类的所有 x i t x_i^t xit的得分之和,因为赋值 a i k t a_{ik}^t aikt是固定的,L’是L的上界,也就是 L ( Y t ) ⩽ L ′ ( Y t ) L(Y^t)\leqslant L'(Y^t) L(Yt)⩽L′(Yt). L ( Y t ) L(Y^t) L(Yt),min是非线性计算,所以直接计算 L ( Y t ) L(Y^t) L(Yt)是非常困难的,我们用 L ′ ( Y t ) L'(Y^t) L′(Yt)来替代。
其中1为指标函数, s − t \stackrel{-t}{s} s−t为未分配到任何聚类的所有 x i t x_i^t xit的得分之和,因为赋值 a i k t a_{ik}^t aikt是固定的,L’是L的上界,也就是 L ( Y t ) ⩽ L ′ ( Y t ) L(Y^t)\leqslant L'(Y^t) L(Yt)⩽L′(Yt). L ( Y t ) L(Y^t) L(Yt),min是非线性计算,所以直接计算 L ( Y t ) L(Y^t) L(Yt)是非常困难的,我们用 L ′ ( Y t ) L'(Y^t) L′(Yt)来替代。
L ′ ( Y t ) L'(Y^t) L′(Yt)可以简写成:
L ′ ( Y t ) = ∑ k ∑ j s − k j d ( y k t , x − k j ) , L'(Y^t)=\displaystyle\sum_{k}\displaystyle\sum_{j}\stackrel{-k}{s}_jd(y_k^{t},\stackrel{-k}{x}_j), L′(Yt)=k∑j∑s−kjd(ykt,x−kj),
s − k j \stackrel{-k}{s}_j s−kj和 x − k j \stackrel{-k}{x}_j x−kj一旦被写成这种形式,我们就可以计算:
y k t = ∑ j s − k j x − k j / ∑ j s − k j y_k^{t}=\displaystyle\sum_{j}\stackrel{-k}{s}_j\stackrel{-k}{x}_j/\sum_{j}\stackrel{-k}{s}_j ykt=j∑s−kjx−kj/j∑s−kj
大意:这个部分我不懂,我的理解是化简 L ′ ( Y t ) L'(Y^t) L′(Yt),规定了 s − k j \stackrel{-k}{s}_j s−kj和 x − k j \stackrel{-k}{x}_j x−kj,但是我不知道这两个是什么含义,知道的小伙伴可以在评论区分享一下。
L ′ ( Y t ) L'(Y^t) L′(Yt)的优化方法请参考2.1节,这里不再赘述。 前面给出了一种从任意Y开始,一帧一帧优化的方法。我们交替向前迭代(从t=1到t=t进行优化)和向后迭代(从t=t到t=1),直到收敛(通常几次就足够了)。为了避免局部极小值,与标准k-均值类似,执行了多次随机初始化。
大意:优化是迭代过程。
2.2变量K
我们的方法可以通过一次迭代估计一个轨迹来自动估计图像或视频中的对象数量K,我们设K=1,用2.2中的方法找到给定X和S的最佳姿势轨迹。去除返回轨迹Y附近的所有估计值 x i t x_i^t xit和相应的分数 s i t s_i^t sit,直到每帧只剩一个估计姿态(或者没有姿态,这种就是画面中没有出现对象)停止迭代。如果 d ( x i t , y t ) < z d(x_i^t,y^t)
Pose_NMS是一种多功能方法。可以合并单个图像或短序列中的姿态,通过参数λ控制时间项所占比例。如果长时间物体数量固定(例如笼子里的动物),可以使K>1进行联合优化,生成一种高效的“重复姿态估计跟踪”方法。可用于跟踪场景(进入/离开场景的对象数量可变),用Pose_NMS在短序列中查找相关轨迹。
大意:说明变量K的含义,就是对象数目,K=1说明图片中只有一个对象,只用估计一个姿态。Pose_NMS的用途广泛,厉害。
以上就是我认为这篇文章中最重要的部分,下面就是实验方法和实验结果,不会逐句翻译,我只讲一下大概,感兴趣的小伙伴可以仔细看原文,它的实验还是非常有技巧性的,而且很全面,为了体现效果,特意选取和自制了一些数据。
3.结果

大意:用到的数据和三个检测任务,对数据进性预处理,确定检测框

大意:四种方法,分别使用这几种方法,对比最后效果
3.1 Buffy stickmen数据集
3.1.1 Original Buffy 数据集没有时间信息

大意:Original Buffy 数据集没有时间信息,Pose_NMS方法比NMS方法效果好
3.1.2 Video Buffy数据集
3.2 Faces
3.3 Mice
4.总结
ps:这篇文章是我学习人体姿态估计看的第二篇论文,目前是小白阶段,解析有很多不足和不专业的地方,请大家多多担待,欢迎感兴趣的朋友一起交流,我会继续分享和记录自己的学习过程,请大家多多支持,为我第一篇博文点个赞。





