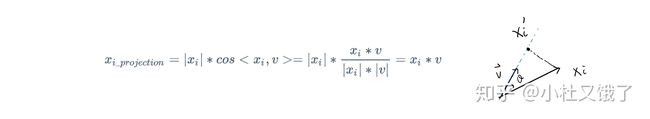pca 累积方差贡献率公式_PCA:从入门到入土到入神
写在前面:
- 看完这篇文章,你会知道:
- ①为什么要用PCA?
- ②PCA的原理?
- ③slearn中的PCA如何使用?
- 资料来源于互联网及课堂讲义;
- 欢迎讨论和补充~
1 背景
1.1 维数灾难
在做数据挖掘的时候,经常会遇到数据体量过大的情况,这种大体量往往会在两方面:
- 样本量过大(表现为行多);
- 样本特征过多(表现为列多);
从而在处理的时候会占用很多时间和空间,耗费大量的成本。
维数灾难(Course of Dimensionality)就是人们在对这种现象抽象化的概念。
对于提高运算效率的需求一直以来都存在——
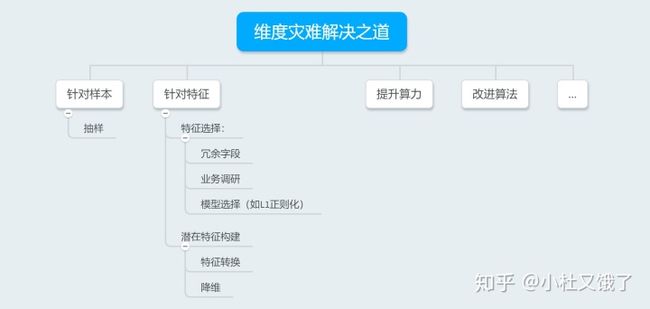
1.2 解决之道
我们的对策往往也是针对行和列,以及算法、算力上进行展开的。
一方面,样本上,通常采用抽样的方法:
- 我们知道样本代表着观测结果。如果没有重复的冗余数据,每一条都可以是有价值的。抽样就是从数据集中选取一小部分的数据进行分析,需要注意的是抽样规则很大程度会影响模型的训练效果(比如在样本不均衡的时候可以采用SMOTE等方法);
另外,特征上,可以进行特征选择和潜在特征构建:
- 特征选择(Feature selection):选取一部分有用或有价值的特征进入模型进行训练;
- 潜在特征构建(Latent feature creation):新建新的字段来描述原本的特征。如对一类特征进行降维处理,使得降维后的数据能够表达原本的信息;
但是,高维数据的低位表达,即降维,必然会来信息的丢失:
2.6.1 主成分分析,数据挖掘:理论与算法(自主模式)如袁博老师提到的例子(上图右侧):将一个三位的圆环从不同角度去观测,并映射到二维平面时,会得到不同的结果。每个结果始终会和原本的圆环有出入。
如果接触不到,那就无限接近。
保留全部信息是一种奢望,那确保降维过程能够尽可能保留原本数据的信息,就成了整个问题的核心。
PCA,Principle Component Analysis,就是一种较为简单和普遍的降维方法——
2 PCA
一句话定义:通过线性线性变换,将数据映射到低维的子空间中的降维方法,期间尽可能防止信息丢失。
2.1 从一个例子开始
问题来了,什么是数据的信息?
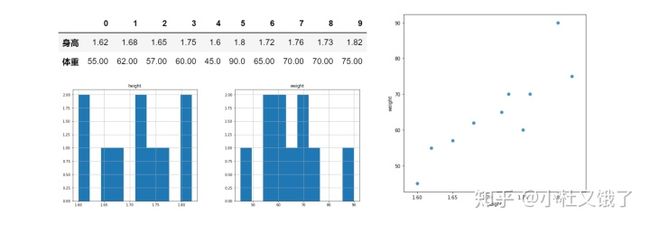
很简单,举个例子,比如一群人的身高体重分布如下:
某组人的身高体重情况我们能够说他们有所不同,正是因为组内,人与人之间的身高体重有差别。
如果一个维度的差别越大,比如身高从1.5m~2m,那可以说组内的信息量就会比较多。反之,如果大家都是1.65m,那我们能从组里得到的信息就很少,几乎没有分析价值。
那保留原本信息的目标就可以转换为保留原本方差,即数据的离散程度。
目标清楚了之后,就可以开始降维了。
它会需要我们重新构建一个基向量,其中包含两方面:方向和位置:
得到方向:将原本的数据映射到不同方向的单位向量上,会有不同的结果。我们有很多种选择,如何获得更好方向的呢?
还是上面的例子(二维往下就是一维啦):
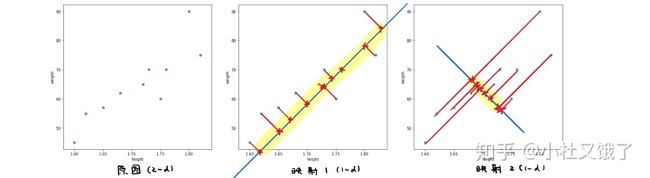
原图(左) 映射一(中) 映射二(右)向中间和右侧的图,可以理解是二维的坐标映射到直线上,成为一维的点。
从结果上看:映射1 中,点的离散程度会比 映射2 更大,映射2 过于紧密了。
回看目标——保留方差,因此,我们可以很直观地看出 映射1 的降维结果会保留更多信息(方差),是更好的降维结果。
当然,这是二维的情况,如果对于高维的化也是同样。我们可以设立这样一个目标:
- 确定降维之后的维度数;
- 找到一个对应维度的子空间(一组相互正交的方向向量),原数据映射到该空间下能最大程度保留其方差;
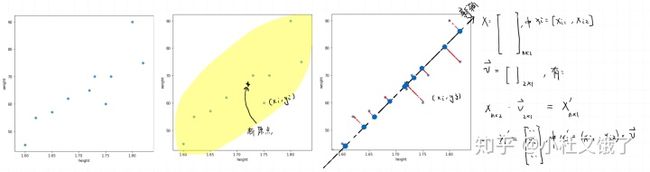
另外,还需要得到位置:从方差公式上我们可以看到,为了能够使得所有的方差计算更加公允
这会需要将每个特征减去它的均值,对于矩阵X而言,就是说:
对于上面的图而言,就是如下图所示的结果,如果之前的映射1是最佳的结果,那么我们就能得到最后的结果了:
其中,每个观测x从原本的二维映射到新的坐标轴上,变成一维时,公式如下:
计算
2.2 梳理一下
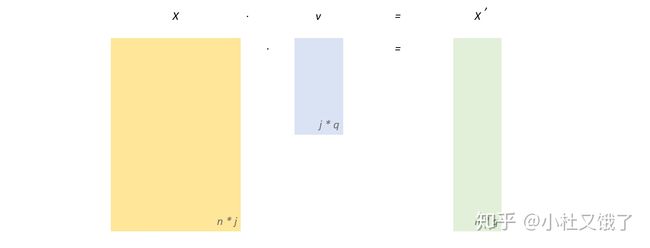
线性代数当中我们学过矩阵相乘的内容,它的本质是线性变换。
遵循的规则是
-
,即
和
有同样的行数,但列数上
更少;
-
中列向量正交;
那么可以说
因此,从上面的流程上看,PCA可以理解成:
- 所有数据中心化处理;
- 将数据映射到子空间中:
- 选择需要保留的信息量 or 选择维度;
- 通过线性变换,根据上述条件进行映射;
- 降维完毕;
- 其输入是原始数据,每个维度有一定现实意义;
- 而输出的结果则是原本每个维度的线性组合,实际意义相对于原来会减少;
2.3 最佳方向
上面的例子当中已经把PCA的流程和内容大致说明了,接下来有个很关键的问题,就是确定每次选择的方向。
首先明确一些基础定义:
- 样本
- 数据集
- 样本
- 矩阵
第一步:构造目标
假定X已经去中心化,X通过与V点积完成线性变换,计算此使得方差,有:
第二部:求导解决
利用拉格朗日乘子法,可以求得:
求解得到:
会发现很眼熟,因为这个等式是求特征值和特征矩阵时候遇到的公式。这里的
-
为特征值;
-
为特征向量;
并且进一步,我们能得到:
所以方差可以由特征值表示。
第三步:梳理
到此为止,我们知道:
- 目标是要解出线性变换规则
;
-
是
的特征向量;
- 方差
可以由特征值
进行表示;
所以为了保留最大的方差,只需要选出最大的几个特征值,并选出特征值对应的主成分(就是
当然,上面的PCA实现过程看起来比较繁琐,在具体应用的时候更多直接是从python当中掉包来降维——
3 Python中的PCA应用
为了能够比较清楚的解释应用方法,来,上python!
这里用鸢尾花的数据集,经典内味:
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
iris = datasets.load_iris()
X = iris['data']
y = iris['target']接下来会先用sklearn实现一次PCA,随后用numpy进行验证之前证明过程中推导的结果:
3.1 sklearn中的pca
初始化pca:
sklearn中的pca有两种初始化pca对象的方式——指定主成分数量初始化和指定保留方差量初始化,从数量开始:
结构为:
pca = PCA(n_components=xxx)鸢尾花的例子中,可以:
print('Before pca: n', X[:3,:])
pca_1 = PCA(n_components=2) # 指定主成分数量初始化
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果
# 这里只展示前三行的结果以示对比
print('After pca: n', X_red_1[:3, :],'n')
# 查看各个特征值所占的百分比
print('explained_variance_ratio_: ', pca_1.explained_variance_ratio_)
# 线性变换规则
print('components_: ', pca_1.components_)会发现,在将为之前的数据是4维,但是pca处理过后就变成了两维。
这里还调用了一些其他的属性和方法:
- fit_transform:能够得到降维后的数据因为pca是无监督的方法,可以这样操作,当然也可以拆开写;
- explained_variance_ratio_:查看每个主成分保留的方差百分比;
- explained_variance_ratio_.sum():当前保留总方差百分比;
- components_:主成分(特征值)对应的特征向量,这个很重要,能够查看数据降维过程中线性变换的规则。在解释性上,对应的,也能够了解每个原本字段在新特征构建过程中的权重(虽然没怎么用过);
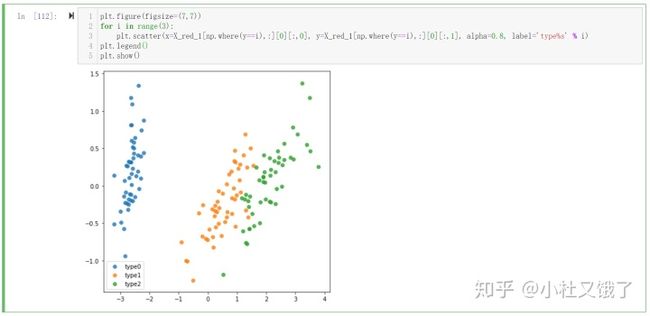
保留维度通常是为了更好的可视化,比如将带标签的高维数据映射到二维或者三维,能够很直接地看到原本数据的大体分布,然后根据这个来选择进一步的方法:
plt.figure(figsize=(7,7))
for i in range(3):
plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='type%s' % i)
plt.legend()
plt.show()第二种,是指定保留方差量初始化。这一种方法可以在降维后查看保留的维度数量等等,比较懒人:
结构为:
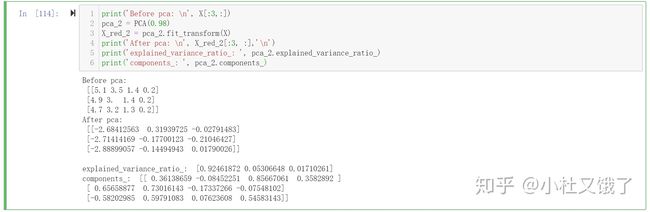
pca = PCA(0.98) # 即保留0.98的信息量(方差)鸢尾花的例子中,可以:
print('Before pca: n', X[:3,:])
pca_2 = PCA(0.98)
# 后续的操作都一样,仅仅在初始化上有区别
X_red_2 = pca_2.fit_transform(X)
print('After pca: n', X_red_2[:3, :],'n')
print('explained_variance_ratio_: ', pca_2.explained_variance_ratio_)
print('components_: ', pca_2.components_)方法同上,但是我们可以发现它在判定的时候将数据降到了3维当中。如果调用explained_variance_ratio_.sum()方法会发现现在有保留0.99+的方差。
那如何做出最开始的选择呢?
# Fitting PCA
pca = PCA()
pca.fit_transform(X)
# 对所有的保留情况进行累加(1个主成分,2个,...直到和原本数据维度相同
explained_var = np.cumsum(pca.explained_variance_ratio_)
# Plotting the amount of variation explained by PCA with different numbers of components
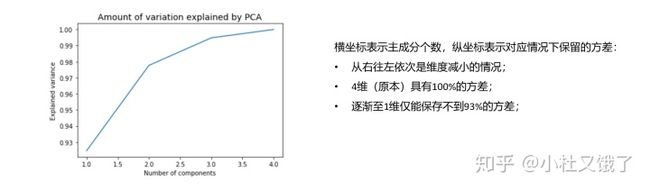
plt.plot(list(range(1, len(explained_var)+1)), explained_var)
plt.title('Amount of variation explained by PCA', fontsize = 14)
plt.xlabel('Number of components')
plt.ylabel('Explained variance')
plt.show()- 可以看到保留2个或者3个都是很不错的选择;
那么以上基本就是sklearn中的pca了。
不过你可能还是会有问号。emmmmmm这不就和没讲一样吗?掉个包就完事儿,当中这么多映射规则,保留方差百分比什么的,和之前证明有什么关系吗?
那就到最后一部分,用numpy来验证我们证明中得到的细节——
3.2 Numpy验证PCA
根据推到步骤,首先我们应该将数据中心化,即每一列都减去当列的均值,需要注意的是,这里只会展示前3个观测(整个数据集有150条)的计算结果:
print(X[:3,:])
for i in range(X.shape[-1]):
X[:,i]-=np.mean(X[:,i])
print(X[:3,:])接下来求X和其转置矩阵的特征值和对应的特征向量,在python中一行就可以搞定:
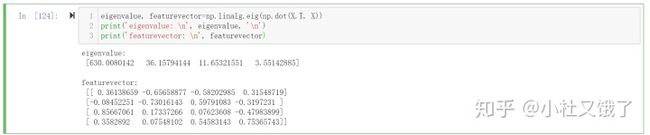
eigenvalue, featurevector=np.linalg.eig(np.dot(X.T, X))
print('eigenvalue: n', eigenvalue, 'n')
print('featurevector: n', featurevector)这个数字是不是感觉有点眼熟?
在特征向量的部分,几个数字和我们之前在pca.components_中看到的一样。
回想推导过程(假定原数据维度是Nxm):
- 因为是单位向量,所以投影和方差一致;
- 我们用拉格朗日数乘法得到,在这种情况下特征值和方差数值相等;
- 根据需求,依次选择最高的k个特征值和对应的特征向量(m*j),即为线性变换规则;
- 将原数据矩阵矩阵(Nxm)中心化后,同选择的特征向量矩阵(mxj)相乘;
- 降维完毕;
回看上面的pca,在保留2维、3维的时候,所乘的矩阵确实由特征值自高往低排列,所对应的特征向量构成。
也就是说,这里印证了最大的几个特征值所对应的特征向量组合在一起,就构成了线性变换的规则,来进行降维映射。
那么接下来,就是选择最大的几个特征值,并得到对应的主成分,进行线性变换,验证一下:
# 保留两个维度进行降维
# 选择两个维度是为了方便可视化
# numpy 验证
dim_map = np.argsort(-eigenvalue)[:2]
vec = featurevector[:, dim_map]
result_np = np.dot(X, vec)
# pca 实现
pca = PCA(n_components=2)
result_pca = pca.fit_transform(X)
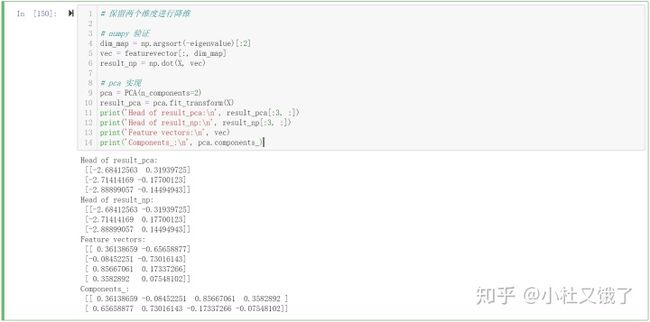
print('Head of result_pca:n', result_pca[:3, :])
print('Head of result_np:n', result_np[:3, :])
print('Feature vectors:n', vec)
print('Components_:n', pca.components_)那么验证成功了,只剩最后一个问题:保留特征百分比是什么?
将特征值转换为占比即可,验证一下:
eigenvalue/eigenvalue.sum(), pca.explained_variance_ratio_验证成功
以上,就是我对PCA的理解
欢迎补充~