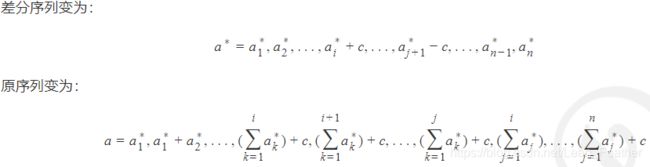关于差分

差分

前言：我还记得曾经为了学这块内容还自己一个人在学校宿舍里自己给自己讲了好几遍......

什么是差分

概念：差分是前缀和的逆运算，是一种简单而巧妙的技巧，常用于优化序列和树的查询操作。

例如序列： 2，7，9，1对应的前缀和序列为：2，9，18，19 。

反过来， 2，9，18，19 对应的差分序列为 2，7，9，1 。

序列差分

对于一个序列的差分，是用当前项的值减去前一项的值。

有关例题：

给出一个长为 n 的序列，有 m 次操作，每次操作对序列一段区间的数加上一个数字，请输出 m 次操作后的序列。

咱还是先考虑考虑朴素（暴力）算法：

对于每次操作，都暴力的枚举对应的区间，将区间中的数加上给定的数字。

具体来说，对于一次要将 [l,r] 区间的数加上 c 的一次操作，我们枚举 al,al+1,...,ar−1,ar ，给他们都加上数字 c 。

void adjust(int l,int r,int c) {
    for(int i = l; i <= r; i++)
        a[i] += c;
}

m 次操作后，枚举序列中的每个数，将其输出出来即可。 当然题目的范围可是你暴力无法承受的，复杂度也不难计算：O(nm)。

差分算法

这回给大家介绍一下用差分的便捷。基本思路：

1. 定义一个数组b；
2. 对于每次操作在区间 [l, r] 加上c， 令 b[l] += c, b[r + 1] -=c;
3. m 次操作结束后，我们求出 b 数组的前缀和数组 b′，将  b′[i] 的值加到 a[i] 上去，此时 a 数组就是我们要求的结果。

#include
#define N 200020
using namespace std;
int n, m, a[N], b[N];
int main(){
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 1; i <= m; i++){
		int l, r, c;
		cin >> l >> r >> c;
		b[l] += c;
		b[r + 1] -= c;
	} 
	for(int i = 1; i <= n; i++)
		b[i] += b[i - 1];
	for(int i = 1; i <= n; i++)
		a[i] += b[i], cout << a[i] << " ";
	return 0;
} 

算法正确性证明

对于序列 a = a1,a2,...,an ，我们定义它的差分序列：

给出一个序列 a ，我们可以根据定义求出它的差分序列。

反过来，给出一个差分序列，我们也可以求出它对应的原序列：

假设这个差分序列是 

 

那么它的对应序列就是

也就是说，差分序列 a∗ 的前缀和序列，就是它的原序列。

那么如果我们给差分序列的第 i 项加 c ，给差分序列的第 j+1 项减 c ，对应的原序列又会发生什么呢：

给差分序列的第 i 项加 c 、第 j+1 项减 c 后，对应的原序列 [l,r] 区间上的数都被加上了 c ！

这是因为原序列是差分序列的前缀和序列，我们在 ai 处加了个 c ，加的这个 c 就会使得 ai 以及之后的元素加 c ；而在 aj+1 处减去了 c ，就会使得 aj+1 及之后的元素减 c 。两相抵消，就只会使得 al,al+1,...,ar−1,ar 加上了 c ，而其他元素不受影响。

有了上面的结论，就能解释我们的差分算法为什么是对的了。

事实上，我们在之前用到的 b 数组，就是一个差分序列。 当我们需要对区间 [l,r] 加上 c 的时候，我们在差分数组中，给 bl+=c,br+1−=c ，就能使得对应的原序列 [l,r] 区间加上 c 。

b 是差分序列，那么 b 的前缀和所对应的序列就是原始序列修改后的结果。

这样做的时间复杂度是多大呢？我们每次操作只要在差分序列中改变两个数的值，因此一次操作的复杂度是 O(1) 的，那么 m 次操作的复杂度即为 O(m) 。加上开始求出差分序列 b 以及最后还原前缀和序列的运算复杂度 O(n) 。因此算法复杂度为 O(m+n) 。

 

结语

今天跟大家分享一句话：

权威首先应该建立在理性的基础上。

                                    ——圣埃克絮佩里《小王子》