2021年度训练联盟热身训练赛第一场

A Weird Flecks, But OK
最小圆覆盖模板题，大部分都是用的板子吧，来个三分套三分吧。（跑得比较慢）

#include 
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const double eps=1e-6;
const int N = 5010, M = 1e6+10;
int n,k;
double x[N],y[N],z[N];

double check3(double a,double b,double x[],double y[]){
     
    double res=0;
    for(int i=1;i<=n;++i){
     
        res=max(res,sqrt((a-x[i])*(a-x[i])+(b-y[i])*(b-y[i])));
    }
    return res;         
}

double check2(double a,double x[],double y[]){
     
    double l=-1e3,r=1e3;
    while(r-l>eps){
     
        double mid1=l+(r-l)/3;
        double mid2=r-(r-l)/3;
        if(check3(a,mid1,x,y)<check3(a,mid2,x,y)) r=mid2;
        else l=mid1;
    }
    return check3(a,l,x,y);
}

double check(double x[],double y[])
{
     
    double l=-1e3,r=1e3;
    while(r-l>eps){
     
        double mid1=l+(r-l)/3;
        double mid2=r-(r-l)/3;
        if(check2(mid1,x,y)<check2(mid2,x,y)) r=mid2;
        else l=mid1;
    }
    return check2(l,x,y);
}

void solve(){
     
    scanf("%d",&n);
    for(int i=1;i<=n;++i) scanf("%lf%lf%lf",x+i,y+i,z+i);
    printf("%.8lf\n",2*min({
     check(x,y),check(x,z),check(y,z)}));
}
int main(){
     
    int _;
    _=1;  
    while(_--){
     
        solve();
    }
    return 0;
}

B Code Names
对可操作的字符串之间建边的话，题意就是选择尽量多的点使得两两之间不相邻，就是最大独立集。一般图的最大独立集不会求，而且原图中一定不会有边为3的环，所以大胆猜测奇环不存在就是二分图。
二分图的最大独立集=总点数-最大匹配数。

//#include 
//#pragma GCC optimize(2)
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define go(i, l, r) for(ll i = (l), i##end = (ll)(r); i <= i##end; ++i)
#define god(i, r, l) for(ll i = (r), i##end = (ll)(l); i >= i##end; --i)
#define ios ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define debug_in  freopen("in.txt","r",stdin)
#define debug_out freopen("out.txt","w",stdout);
#define pb push_back
#define all(x) x.begin(),x.end()
#define fs first
#define sc second
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,ll> pii;
const ll maxM = 1e6+10;
const ll inf_int = 1e9+10;
const ll inf_ll = 1e17;

void read(int &x){
     
    scanf("%d",&x);
}
void read(ll &x){
     
    scanf("%lld",&x);
}
template<class H, class... T> void read(H& h, T&... t) {
     
    read(h);
    read(t...);
}

void pt(){
      cout<<'\n';}
template<class H, class ... T> void pt(H h,T... t){
      cout<<" "<<h; pt(t...);}

//--------------------------------------------
const int maxn = 1e3+10;
int n, m;
vector<int> G[maxn];
string s[maxn];

int match[maxn];
bool vis[550];
bool find(int a){
     
    for(auto u:G[a]){
     
        if(!vis[u]){
     
            vis[u]=true;
            if(match[u]==0||find(match[u])){
     
                match[u]=a;
                return true;
            }
        }
    }
    return false;
}
void init(){
     
    for(int i = 1;i<=n;i++){
     
        for(int j = i+1;j<=n;j++){
     
            int cnt = 0;
            for(int k = 0;k<s[i].size();k++){
     
                if(s[i][k] == s[j][k]) cnt++;
            }
            if(cnt == s[i].size()-2){
     
                G[i].pb(j); //pt(i,j);
                G[j].pb(i);
            }
        }
    }
}
int main() {
     
    read(n);
    for(int i = 1;i<=n;i++) cin>>s[i];
    init();
    int ans=0;
    for(int i=1;i<=n;i++){
     
        memset(vis,0,sizeof vis);
        if(find(i)){
     
            ans++;
        }
    }
    cout<<n - ans/2<<'\n';
    return 0;
}

C New Maths
a⊗b 就是不进位的乘法
举个栗子：
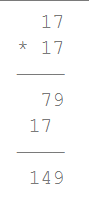（加和乘都不进位）
所以 a⊗a的位数就是 a的位数的二倍再减一
所以a最多13位，且乘积的位数只能是奇数。所以爆搜试一试。

#include
using namespace std;
typedef long long ll;
const int N=50;
int n;
char s[N];
int a[N],b[N];
bool check(int k){
     
	int res=0;
	for(int i=0;i<=k;++i) res=(res+b[i]*b[k-i])%10;
	return res==a[k];
}
ll ans=1e18;
void get_max(){
     
	for(int i=n;i<n*2-1;++i)
		if(!check(i)) return ;
	ll res=0,p=1;
	for(int i=0;i<n;++i) res=res+b[i]*p,p*=10;
	ans=min(ans,res);
}
void dfs(int x){
     
	if(x==n){
     
		get_max();
		return ;
	}
	for(int i=0;i<=9;++i){
     
		b[x]=i;
		if(check(x)){
     
			dfs(x+1);
		}
	}
}
void solve(){
     
    scanf("%s",s);
	n=strlen(s);
	if(n%2==0){
     
		puts("-1");
		return ;
	}
	for(int i=0;i<n;++i) a[n-i-1]=s[i]-'0';
	n=(n+1)/2;
	dfs(0);
	cout<<(ans==1e18?-1:ans)<<endl;
}

int main(){
     
	 int _;
    _=1;  
    while(_--){
     
        solve();
    }
    return 0;
}

E Early Orders
我们从前向后依次选择一个数加入序列，当已经选择i个数时，选择下一个数时我们有两个集合分别是：已经选择过的数和未选择过的数。
假设上个数选择的位置是l，那么我们需要找到一个位置r使得未选择的数在r之后全部出现过，那么区间（l，r ]的所有数都是可以选的，不会使接下来选不到某些数，而且为了使得字典序最小，我们需要选择区间内的最小值。
last[i]表示数字i最后出现的位置，那么r 就是未选择集合的最小值，可以对所有的last取最小值，选择一个数之后就将它的last置为inf，线段树即可维护。
那么就剩如何求区间(l,r]的最小值，如果区间有多个最小值时需要选择最左边的哪一个使得 l 尽量小，后续选择范围尽量大以使得字典序更小，那么可以建一个堆来维护，每次选择之前将区间所有值全部添加（因为下一个 r 一定比当前r要大），然后将不属于区间的剔除，选择一个区间的最小值。

//#include 
//#pragma GCC optimize(2)
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define go(i, l, r) for(ll i = (l), i##end = (ll)(r); i <= i##end; ++i)
#define god(i, r, l) for(ll i = (r), i##end = (ll)(l); i >= i##end; --i)
#define ios ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define debug_in  freopen("in.txt","r",stdin)
#define debug_out freopen("out.txt","w",stdout);
#define pb push_back
#define all(x) x.begin(),x.end()
#define fs first
#define sc second
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,ll> pii;
const ll maxM = 1e6+10;
const ll inf_int = 1e9+10;
const ll inf_ll = 1e17;

void read(int &x){
     
    scanf("%d",&x);
}
void read(ll &x){
     
    scanf("%lld",&x);
}
template<class H, class... T> void read(H& h, T&... t) {
     
    read(h);
    read(t...);
}

void pt(){
      cout<<'\n';}
template<class H, class ... T> void pt(H h,T... t){
      cout<<" "<<h; pt(t...);}

//--------------------------------------------
const int maxn = 2e5+10;
int n,k;
int a[maxn];
struct node2{
     
    int w,id;
    bool operator <(const node2 & o) const{
     
        if(w != o.w) return w > o.w;
        else return id > o.id;
    }
};
bool vis[maxn];
priority_queue<node2> q;
struct node{
     
    int l,r;
    int mi;
}tr[maxn*4];

void pushup(int u){
     
    tr[u].mi = min(tr[u << 1].mi, tr[u << 1 | 1].mi);
}
void build(int u,int l,int r){
     
    tr[u] = {
     l,r};
    if(l == r) return ;
    int mid = l+r>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
}

void modify(int u,int idx,int v){
     
    if(idx == tr[u].l && idx == tr[u].r) tr[u].mi = v;
    else{
     
        int mid = tr[u].l+tr[u].r>>1;
        if(idx<=mid) modify(u<<1,idx,v);
        else modify(u<<1|1,idx,v);
        pushup(u);
    }
}
int main() {
     

    read(n,k);
    build(1,1,k);
    for(int i = 1;i<=n;i++) {
     
        read(a[i]);
        modify(1,a[i],i);
    }
    int ll = 1;
    vector<int> ans;
	for(int i=1,l=0,r=0;i<=k;++i){
     
		r=tr[1].mi;
		while(l<r) q.push({
     a[l+1],l+1}),l++;
		while(q.size()){
     
			node2 cur = q.top();q.pop();
			if(cur.id < ll || vis[cur.w]) continue;
			else {
     
				ans.pb(cur.w);
				vis[cur.w] = 1;
				modify(1,cur.w,inf_int);
				ll = cur.id+1;
				break;
			}
		}
	}
    for(auto v:ans) printf("%d ",v);
    return 0;
}                      

补：
G Birthday Paradox
m等于总人数。总的情况数就是 $365^m$，先对n个组分配日期就是 ${\prod }_{i=365-n+1}^{365}i$ ,然后就是将m个人分成输入的组，假设隔板是定的，那么先将m个人全排列就是 m！，再排除组内相同的排列就是
$\frac{m!}{\prod a[i]!}$ ,然后相同数量的组也是重复的，就是
$\frac{m!}{(\prod a[i]!)\ast (\prod num[j])}$

#include
using namespace std;
typedef long long ll;
const int N=200100;
int n,a[N];
int sum=0;

double log10(double x){
     
	return log(x)/log(10);
}
double A[40010];
double c(int n,int m){
     
	return A[n]-A[m]-A[n-m];
}
int num[N];
int main(){
                                       
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",a+i),sum+=a[i],num[a[i]]++;
	for(int i=1;i<=40000;++i) A[i]=A[i-1]+log10(i);
	double ans=0;
	for(int i=1;i<=n;++i){
     
		ans=ans+log10(365-i+1)-A[a[i]];
	}
	for(int i=1;i<=sum;++i) ans-=log10(365);
	ans+=A[sum];
	for(int i=1;i<=100;++i)
		if(num[i]) ans-=A[num[i]];
	printf("%.10lf",ans);
}

I 换根dp模板题，记得之前训练联盟好像有一道一样的，可惜没看懂题意，看懂也没时间了。。。

#include
using namespace std;
typedef long long ll;
const int N=200100;
int n,t[N];
ll sum[N],f[N],p[N],d[N],ans[N];
int h[N],e[N],w[N],ne[N],idx;
void add(int a,int b,int c){
     
	e[idx]=b;ne[idx]=h[a];w[idx]=c;h[a]=idx++;
}
ll sz[N];
void dfs(int u,int fa){
     
	sz[u]=1;
	sum[u]=t[u];
	for(int i=h[u];~i;i=ne[i]){
     
		int v=e[i];
		if(v==fa) continue;
		dfs(v,u);
		sz[u]+=sz[v];
		sum[u]+=sum[v];
		d[u]+=d[v]+sz[v]*w[i];
		f[u]+=f[v]+sum[v]*w[i];
	}
}
void dfs1(int u,int fa){
     
	ans[u]=f[u]+t[u]*d[u];
	for(int i=h[u];~i;i=ne[i]){
     
		int v=e[i];
		if(v==fa) continue;
		f[v]=f[v]+(f[u]-f[v]-sum[v]*w[i])+(sum[u]-sum[v])*w[i];
		sum[v]=sum[u];
		d[v]=d[v]+(d[u]-d[v]-sz[v]*w[i])+(n-sz[v])*w[i];
		dfs1(v,u);
	}
}
int main(){
     
	memset(h,-1,sizeof h);
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",t+i);
	for(int i=1;i<n;++i){
     
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);add(b,a,c);
	}
	dfs(1,-1);dfs1(1,-1);
	for(int i=1;i<=n;++i) printf("%lld\n",ans[i]);
}

K放弃了，溜了溜了