计算几何基础知识整理 代码模板与证明过程
计算几何基础知识
一、求 π \pi π的方法
我们在代码中一般把 π \pi π记作PI,PI = acos(-1)。因为我们都知道cos( π \pi π) = -1,所以PI = arccos(-1)。
acos()
二、余弦定理
c^2 = a^2 + b^2 - 2acos(t);三、向量
(1)向量的加、减、数乘运算
计算:坐标分别直接相加减乘。
对应几何意义:平行四边形法则。
(2)向量的内积
内积也称作点积: a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ c o s θ \vec a \cdot \vec b = |\vec a| \cdot |\vec b| \cdot cos\theta a⋅b=∣a∣⋅∣b∣⋅cosθ
数学计算:就是x、y坐标分别相乘再相加即可。即若 a ⃗ = ( x 1 , y 1 ) , b ⃗ = ( x 2 , y 2 ) \vec a = (x_1,y_1),\vec b = (x_2,y_2) a=(x1,y1),b=(x2,y2) 。则 a ⃗ ⋅ b ⃗ = x 1 × x 2 + y 1 × y 2 \vec a \cdot \vec b = x_1 \times x_2 + y_1 \times y_2 a⋅b=x1×x2+y1×y2 。内积得到的答案是一个数值。
几何意义: 向量A、B的内积就等于向量A在向量B上的投影长度乘向量B的长度。
代码实现
double dot(Point a,Point b)
{
return a.x * b.x + a.y * b.y;
}(3)向量的外积
外积也称作叉积: a ⃗ × b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ s i n θ \vec a \times \vec b = |\vec a| \cdot |\vec b| \cdot sin\theta a×b=∣a∣⋅∣b∣⋅sinθ
数学计算: a ⃗ × b ⃗ = x 1 × y 2 − x 2 × y 1 \vec a \times \vec b = x_1 \times y_2 - x_2 \times y_1 a×b=x1×y2−x2×y1
几何意义: 外积求出来的是以向量A和B为两边的三角形面积的两倍,也就是以向量A和B为两边的平行四边形面积。这里求出来的面积是个有向面积,是分正负的,与角度有关。
叉积的前后顺序是有要求的,交换顺序后的答案是相反的,因为他计算的是有向面积,他取的角度是前者逆时针旋转到后者的角度为 θ \theta θ,而不单纯的是二者的夹角。 u ⃗ × v ⃗ = − ( v ⃗ × u ⃗ ) \vec u \times \vec v = -(\vec v \times \vec u) u×v=−(v×u)
代码实现
double cross(Point a,Point b)
{
return a.x * b.y - b.x * a.y;
}(4)向量常用函数
1、求向量的模
∣ a ⃗ ∣ = a ⃗ ⋅ a ⃗ |\vec a| = \sqrt{\vec a \cdot \vec a} ∣a∣=a⋅a
double len(Point a)
{
return sqrt(dot(a,a));
}2、计算两向量夹角
c o s θ = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos\theta = \frac{\vec a \cdot \vec b}{|\vec a||\vec b|} cosθ=∣a∣∣b∣a⋅b
double angle(Point a,Point b)
{
return acos(dot(a,b) / len(a) / len(b));
}3、计算两向量构成的平行四边形有向面积
S 平 行 四 边 形 = a ⃗ × b ⃗ S_{平行四边形} = \vec a \times \vec b S平行四边形=a×b
double area(Point a,Point b)
{
return cross(a,b);
}4、求向量A顺时针旋转角度 θ \theta θ后的向量
记原向量A = (x,y),旋转后 θ \theta θ角度后的向量是(x’,y’)
则有 ( x ′ , y ′ ) = ( x , y ) [ c o s θ − s i n θ s i n θ c o s θ ] (x',y') = (x,y)\left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] (x′,y′)=(x,y)[cosθsinθ−sinθcosθ]
在计算机上记 θ \theta θ角的大小为angle
Point rotate(Point a,double angle)
{
return Point(a.x * cos(angle) + a.y * sin(angle) , -a.x * sin(angle) + a.y * cos(angle));
}四、点与直线
(1)直线的表示形式
①一般式:ax + by + c = 0 //可以处理所有直线
②斜截式:y = kx + b //较为直观,但无法处理竖直的直线,需特判竖直线
③点向式:p0 + tv //最常见,这里的p0是直线上的一点,v是平行直线的一个向量。每一个t对应直线上的一个点(2)判断点是否在直线上
随意取直线上一个非零向量(或两点),做一个向量起点到该点的向量,判断这两个向量叉积是否为0。
为0说明其组成的平行四边形面积是0,说明点在直线上;不为0说明点不在直线上。
bool on_line(Point p,Point a,Point b)
{
Vector v = b - a,u = p - a;
if(cross(v,u) == 0)
return 1;
else
return 0;
}(3)判断点是否在线段上
首先先判断ab向量和ap向量的叉积是否为0,和直线一样先判断是否共线;然后就要判断p在线段上还是在线段两边,这里我们只需要判断ap向量和bp向量的方向即可,只要这两向量是反向的,就说明p在ab中间,在线段上,这通过两向量的点积来判断,若点积小于等于0,说明是反向的,在线段上。
bool on_segment(Point p,Point a,Point b)
{
Vector v = b - a,u = p - a,l = p - b;
return (cross(v,u) == 0 && dot(u,l) <= 0);
}(4)判断两直线是否相交,求交点
若cross(v,w) == 0,则两直线平行或重合,否则可求交点(直线一般用点向式表示)
Point intersection(Point a,Vector v,Point q,Vector w) //点向式表示直线
{
Vector u = p - q;
double t = cross(w,u) / cross(v,w);
return p + v * t;
}证明:证明过程在这里
(5)点到直线的距离
double distance_line(Point p,Point a,Point b)
{
Vector v1 = b - a,v2 = p - a;
return fabs(cross(v1,v2) / len(v1));
}这里是已知直线上任意两点a、b,求p到直线的距离
证明:证明过程在这里
(6)点到线段的距离
double distance_segment(Point p,Point a,Point b)
{
if(a == b)
return len(p-a);
Vector v1 = b - a,v2 = p - a,v3 = p - b;
if(dot(v1,v2) < 0)
return len(v2);
if(dot(v1,v3) > 0)
return len(v3);
return distance_line(p,a,b);
}证明:证明过程在这里。
(7)点在直线上的投影
Point projection(Point p,Point a,Point b)
{
Vector v = b - a,u = p - a;
return a + v * (dot(v,u) / dot(v,v));
}证明:证明过程在这里
(8)判断线段是否相交
已知两线段 a 1 a 2 a_1a_2 a1a2和 b 1 b 2 b_1b_2 b1b2,判断是否相交
bool segment_intersection(Point a1,Point a2,Point b1,Point b2)
{
double c1 = cross(a2 - a1,b1 - a1), c2 = cross(a2 - a1,b2 - a1);
double c3 = cross(b2 - b1,a2 - b1), c4 = cross(b2 - b1,a1 - b1);
return (c1 * c2 <= 0 && c3 * c4 <= 0);
}证明:证明过程在这里
计算几何之多边形
一、三角形
(1)三角形的面积
求三角形面积分为两种情况,若给的是顶点坐标,就用叉积法来求,若给的是三边长,就用海伦公式来求。
海伦公式
已知三边长为a、b、c。
p = (a+b+c) / 2;
s = sqrt(p * (p-a) * (p-b) * (p-c));(2)三角形的四心
1、外心
外接圆圆心。三边中垂线交点,外心到三顶点的距离相等。
2、内心
内接圆圆心。三条角平分线交点,内心到三边的距离相等。
3、垂心
三条高的交点
4、重心
三条中线的交点
(重心的两个性质:1、他是到三角形三顶点距离的平方和最小的点。2、他也是三角形内部到三边距离之积最大的点)
二、凸多边形
(1)定义
凸多边形是指过多边形的任意一边做一条直线,如果其他各个顶点都在这条直线的同侧,则把这个多边形叫做凸多边形
(2)凸多边形的性质
1、任意凸多边形的外角和均为360°
2、任意凸多边形的内角和为(n-2)180°
三、多边形
(1)求多边形的面积
任取平面上一点P,然后逆时针依次枚举多边形的每条边,用点P到该边起点 的向量叉乘该边,将所有答案相加就是该多边形的面积的两倍,如下图:
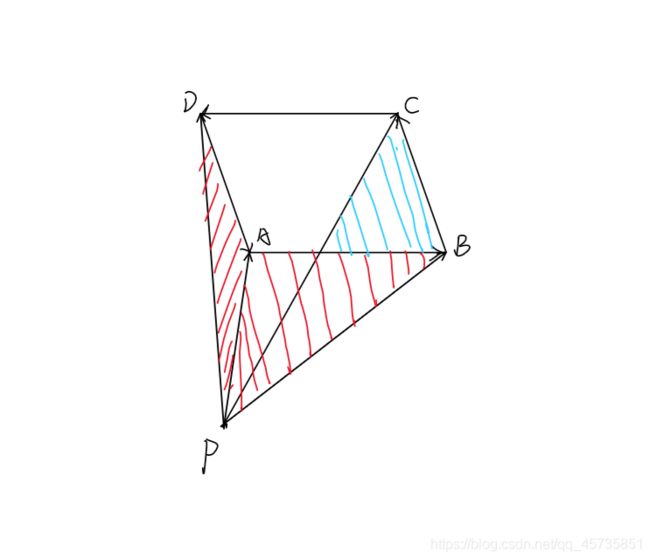
如图: S 平 行 四 边 形 A B C D = P A ⃗ × A B ⃗ + P B ⃗ × B C ⃗ + P C ⃗ × C D ⃗ + P D ⃗ × D A ⃗ 2 S_{平行四边形ABCD} = \frac{\vec {PA} \times \vec{AB} + \vec{PB} \times \vec{BC} + \vec{PC} \times \vec{CD} + \vec{PD} \times \vec{DA}}{2} S平行四边形ABCD=2PA×AB+PB×BC+PC×CD+PD×DA
我们一般选取多边形的一个顶点p[0]作为定点,便于计算,因为叉积得到的是有向面积,所以红色的是被减去的,蓝色的是加上的,最后枚举完所有边后,得到的有向面积就是多边形的面积(可以自己画图试一下)。
代码模板
//求面积的方法有很多,这里给两个方法
//方法一:枚举每个点,这里取原点o作为定点方便计算
double polygon_area(Point p[],int n)
{
double s = 0;
for(int i = 1;i < n;i++)
s += cross(p[i],p[i-1]); //cross是计算叉积
s += cross(p[n-1],p[0]);
return s / 2;
}
//方法二:枚举多边形的每条边,如上图
double polygon_area(Point p[],int n)
{
double s = 0;
for(int i = 1;i < n-1;i++)
s += cross(p[i] - p[0],p[i+1] - p[i]);
return s / 2;
}(2)判断点是否在多边形内
①射线法:从该点出发,任意做一条和边不平行的射线,若射线和多边形交点个数是奇数,说明在内部;若为偶数,说明在外部。
②转角法:从该点依次向多边形每个顶点做向量,然后判断转过的角度是不是360°,若是,则在内部;否则在外部。
③(若该多边形是凸多边形)则可判断该点是不是在所有边的左侧即可。可以用向量的叉积判断左侧。
(3)皮克定理
皮克定理是计算格点中的多边形面积公式,格点是指所有点坐标都为整数的点。
S = a + b 2 − 1 S = a + \frac b 2 - 1 S=a+2b−1
这里的a是多边形内部格点的个数,b是多边形边上格点的个数。