【Vector3】2021-r126版three.js中Vector3类的学习(基于文档与源码)
【Vector3】2021-r126版three.js中Vector3类的学习(基于文档与源码)
目录
-
- 【Vector3】2021-r126版three.js中Vector3类的学习(基于文档与源码)
- 1、构造函数
- 2、方法
-
- 2.1 加减乘除(数值运算)
-
- 2.1.1 加法运算(平移)
- 2.1.2 减法运算(平移)
- 2.1.3 "乘法"运算(缩放)
- 2.1.4 "除法"运算(缩放)
- 2.2 各种变换
-
- 2.2.1 轴角applyAxisAngle(仅旋转)
- 2.2.2 欧拉角applyEuler(仅旋转)
- 2.2.3 轴角与欧拉角的对比
- 2.2.4 四元数applyQuaternion(仅旋转)
- 2.2.5 用四元数取代矩阵解决欧拉角万向节死锁
- 2.2.6 3x3矩阵与4x4矩阵(涵盖多种变换)
- 2.3 基于某种方式设置向量属性(xyz值)
-
- 2.3.1 基于笛卡尔坐标系设置xyz值
- 2.3.2 基于圆柱或球坐标系设置xyz值
- 2.3.3 基于矩阵设置xyz值
- 2.3.4 在原向量方向的基础上改变向量长度
- 3、方法的应用场景分析
【 写在最前面,threejs中向量的各种运算,并不完全是严格按照数学意义来定的,更多是作为一种工具去使用,例如数学中向量并没有所谓除法运算,但Vector3的方法中是有“除法”的,总之,会用这个工具操纵向量达成目标即可。】
three.js中有关vector3的文档地址:threejs官方文档中的Vector3类
线代的几何意义视频(讲的生动有趣建议看看):线性代数的本质(几何意义)Essence of linear algebra
1、构造函数
先看构造函数:
function Vector3(x, y, z) {
if (x === void 0) {
x = 0;
}
if (y === void 0) {
y = 0;
}
if (z === void 0) {
z = 0;
}
this.x = x;
this.y = y;
this.z = z;
}
可见一个向量(或称三维空间中的一个点)仅包含3个属性,即x,y,z,传入要按照xyz的顺序来。
threejs提供了很多便利的点与方向的计算方法,下面分成几类来学习。
2、方法
2.1 加减乘除(数值运算)
2.1.1 加法运算(平移)
| 方法 | 用途 |
|---|---|
| .add ( v : Vector3 ) : this | 将传入的向量v和这个向量相加。 |
| .addScalar ( s : Float ) : this | 将传入的标量s和这个向量的x值、y值以及z值相加。 |
| .addScaledVector ( v : Vector3, s : Float ) : this | 将所传入的v与s相乘所得的乘积和这个向量相加。 |
| .addVectors ( a : Vector3, b : Vector3 ) : this | 将该向量设置为a + b。 |
下面分析源码时,如果不是特殊的传入参数,则不作解释,传参类型在表格中有给出。
从上到下依次看源码,可以看到,加法在代码层面都蛮简单的。
(补充:唯一要注意的是,源码add显示可以传入两个参数,文档对add的解释却是仅可传入一个参数,这里抛出的warn给出了答案,应该是过去的版本支持两个参数吧。)
_proto.add = function add(v, w) {
if (w !== undefined) {
console.warn('THREE.Vector3: .add() now only accepts one argument. Use .addVectors( a, b ) instead.');
return this.addVectors(v, w);
}
this.x += v.x;
this.y += v.y;
this.z += v.z;
return this;
};
_proto.addScalar = function addScalar(s) {
this.x += s;
this.y += s;
this.z += s;
return this;
};
_proto.addVectors = function addVectors(a, b) {
this.x = a.x + b.x;
this.y = a.y + b.y;
this.z = a.z + b.z;
return this;
};
_proto.addScaledVector = function addScaledVector(v, s) {
this.x += v.x * s;
this.y += v.y * s;
this.z += v.z * s;
return this;
};
下面稍微分析下向量加法的几何意义,如下图所示,黄向量+红向量,其实就等于黄向量的点,朝着浅粉这个方向,移动红向量的长度,也就是说,向量的加法其实是点朝着某个向量的方向移动而已。
通常向量都是由原点出发的,但在空间中,它可以在任何位置出现,表达的是同一个方向,因此,这里黄+红向量,等价于将红向量移动至粉向量处,然后黄向量的点沿粉向量移动一段距离。
而黄色方向+粉色方向,等价于深粉方向,也就是两次平移操作等价于一个平移操作,这就是向量加法。
因此,在思考一个点该朝哪个方向移动时,可以基于坐标轴原点来思考,再将其与点相加,即可让该点朝着该方向移动。(加上两倍的向量意为朝着向量方向移动两倍距离)

2.1.2 减法运算(平移)
| 方法 | 用途 |
|---|---|
| .sub ( v : Vector3 ) : this | 从该向量减去向量v。 |
| .subScalar ( s : Float ) : this | 从该向量的x、y和z中减去标量s。 |
| .subVectors ( a : Vector3, b : Vector3 ) : this | 将该向量设置为a - b。 |
跟加法如出一辙,看源码。其实还是平移,只不过是向指定向量的反方向平移,不多赘述。
_proto.sub = function sub(v, w) {
if (w !== undefined) {
console.warn('THREE.Vector3: .sub() now only accepts one argument. Use .subVectors( a, b ) instead.');
return this.subVectors(v, w);
}
this.x -= v.x;
this.y -= v.y;
this.z -= v.z;
return this;
};
_proto.subScalar = function subScalar(s) {
this.x -= s;
this.y -= s;
this.z -= s;
return this;
};
_proto.subVectors = function subVectors(a, b) {
this.x = a.x - b.x;
this.y = a.y - b.y;
this.z = a.z - b.z;
return this;
};
2.1.3 "乘法"运算(缩放)
| 方法 | 用途 |
|---|---|
| .multiply ( v : Vector3 ) : this | 将该向量与所传入的向量v进行相乘。 |
| .multiplyScalar ( s : Float ) : this | 将该向量与所传入的标量s进行相乘。 |
| .multiplyVectors ( a : Vector3, b : Vector3 ) : this | 按照分量顺序,将该向量设置为和a * b相等。 |
先看multiply的源码,可见multiply方法定义的向量相乘,实际上仅是数值相乘,而该方法等价于将一个纯缩放矩阵作用于向量(如果各个缩放尺度一致,则为统一缩放,否则模型将会变形)。
_proto.multiply = function multiply(v, w) {
if (w !== undefined) {
console.warn('THREE.Vector3: .multiply() now only accepts one argument. Use .multiplyVectors( a, b ) instead.');
return this.multiplyVectors(v, w);
}
this.x *= v.x;
this.y *= v.y;
this.z *= v.z;
return this;
};
接下来看multiplyScalar 的源码,由于是乘以统一的标量,因此,该方法等价于将一个统一缩放矩阵作用于向量。
_proto.multiplyScalar = function multiplyScalar(scalar) {
this.x *= scalar;
this.y *= scalar;
this.z *= scalar;
return this;
};
接下来是multiplyVectors的源码:
_proto.multiplyVectors = function multiplyVectors(a, b) {
this.x = a.x * b.x;
this.y = a.y * b.y;
this.z = a.z * b.z;
return this;
};
道理差不多的,只不过不是作用于this,而是传入两个向量做计算,可以视为将b作用于a,对a进行了缩放,或将a作用于b,对b进行了缩放。
补充:这里贴一下缩放矩阵,方便理解,如下图,斜对角线上为各个维度的缩放尺度,当三个数相等时,模型将会作统一缩放,即形状不变,只是变大了,否则模型将会变形,变长,变扁扁之类的。
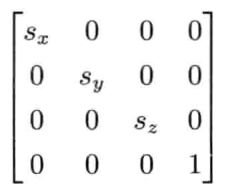
2.1.4 "除法"运算(缩放)
(注:与上文乘法类似,如果对模型整体应用该方法,同样会导致变形)
| 方法 | 用途 |
|---|---|
| .divide ( v : Vector3 ) : this | 将该向量除以向量v。 |
| .divideScalar ( s : Float ) : this | 通将该向量除以标量s。如果传入的s = 0,则向量将被设置为( 0, 0, 0 ) |
看源码,跟乘法差不多,只是少了一个将this设置为两向量相除而已,不多赘述。
_proto.divide = function divide(v) {
this.x /= v.x;
this.y /= v.y;
this.z /= v.z;
return this;
};
_proto.divideScalar = function divideScalar(scalar) {
return this.multiplyScalar(1 / scalar);
};
2.2 各种变换
| 方法 | 用途 |
|---|---|
| .applyAxisAngle ( axis : Vector3, angle : Float ) : this | 将轴和角度所指定的旋转应用到该向量上。 |
| .applyEuler ( euler : Euler ) : this | 通过将Euler(欧拉)对象转换为Quaternion(四元数)并应用, 将欧拉变换应用到这一向量上。 |
| .applyMatrix3 ( m : Matrix3 ) : this | 将所传入的v与s相乘所得的乘积和这个向量相加。 |
| .applyMatrix4 ( m : Matrix4 ) : this | 将该向量乘以四阶矩阵m(第四个维度隐式地为1),并按视角划分。 |
| .applyNormalMatrix ( m : Matrix3 ) : this(还没分析) | 将该向量乘以法线矩阵m并将结果归一化。 |
| .applyQuaternion ( quaternion : Quaternion ) : this | 将Quaternion变换应用到该向量。 |
2.2.1 轴角applyAxisAngle(仅旋转)
(注:变换包括平移,旋转,缩放,切变;轴角,欧拉角与四元数仅表示旋转)
下面一个个看源码,轴角法,即,以一个向量定义旋转轴,再加一个旋转角度来定义旋转,比如,如果用(0,1,0)(即y轴)来表示旋转轴,那么就是绕着y轴的旋转。
从源码可以看出,轴角无法直接作用于点,它需要转换为四元数后,使用四元数来完成旋转,这里用到了基于轴角转换四元数的方法(setFromAxisAngle),以后会另开一篇博文介绍四元数的方法,这里只要知道这是为了转换为四元数即可(四元数或矩阵可以直接作用于点)。
_proto.applyAxisAngle = function applyAxisAngle(axis, angle) {
return this.applyQuaternion(_quaternion.setFromAxisAngle(axis, angle));
};
2.2.2 欧拉角applyEuler(仅旋转)
而欧拉角意为,任意一个旋转,都可拆分为绕三根主轴(模型的x,y,z轴)的旋转,旋转角度包括3个,可称为偏航,俯仰,与滚动,这样的称呼是基于飞机模型来定的,因为是一种较为形象的描述方法,现在也比较常用了。
从源码中可以看出,欧拉角也无法直接作用于点,同样需要转换为四元数,只不过转换所使用的方法为基于欧拉角(setFromEuler)。
_proto.applyEuler = function applyEuler(euler) {
if (!(euler && euler.isEuler)) {
console.error('THREE.Vector3: .applyEuler() now expects an Euler rotation rather than a Vector3 and order.');
}
return this.applyQuaternion(_quaternion.setFromEuler(euler));
};
补充:上面那些方法的传参都是3维向量类或浮点数,就没用多做说明,而applyEuler 有所改变,传入为euler(欧拉角),欧拉角是一个新的类(threejs文档中的euler类),专门用于表示欧拉角,有空另起一篇文章讲下。
2.2.3 轴角与欧拉角的对比
欧拉角与轴角的区别在于,轴角法不会遇到万向节死锁问题,储存需要4个浮点值(3个数表示轴,1个表示角),欧拉角的储存仅需3个浮点数(但在threejs里,由于还需要指定该欧拉角的旋转顺序(注:由于向量乘法不满足交换律,所以旋转矩阵乘法的顺序会影响旋转的结果),因此还要多存个字符串),此外,欧拉角会面临万向节死锁问题(关于万向节死锁,详见如何脱离数学推导理解欧拉角与万向节死锁),以及,欧拉角与轴角均无法直接作用于点,都需要转换为四元数或旋转矩阵才能作用到点上。
2.2.4 四元数applyQuaternion(仅旋转)
接下来讲下四元数,四元数是加速旋转计算的方法,要在数学层面或者几何意义上去理解它有一定的困难,这里放一个生动形象的科普视频,感兴趣可以看下四元数的可视化
放下《游戏引擎架构》关于四元数的一段原文,可以看到这里提到,传统基于矩阵的旋转计算存在3个问题:
1、占用储存空间。 2、性能相对较低。 3、难以计算插值。
因此引入了四元数作为其余旋转方法的代替,并且也是目前最流行的方法。

此外,四元数还可以用于避免基于欧拉角旋转导致的万向节死锁问题,然而我们还是可以使用欧拉角的,只不过在计算时,不是将欧拉角转换为三个旋转矩阵再作用于向量,而是将欧拉角转换为四元数再作用于向量。
2.2.5 用四元数取代矩阵解决欧拉角万向节死锁
这里要再强调一下,基于欧拉角导致万向节死锁,本质上是基于三个连续相乘的旋转矩阵导致的死锁,也就是用了三个表示绕三根主轴旋转的旋转矩阵,作用到一个向量上,这样的计算方式会导致出现死锁。然而,用欧拉角计算出四元数,再把四元数作用在向量上,这样是不会导致死锁的,因为这个本质等于,按照给出的欧拉角计算出了旋转轴,然后按照一根旋转轴来进行了旋转,因此,这就并不是将一个旋转拆分为3个旋转来运算,就不会出现死锁现象。
但是!
这里看一下欧拉角转四元数中,判断旋转顺序的源码,可以发现,可转四元数的顺序不包括重复的,也就是类似XYX这样的顺序,因此如果要实现诸如XYX,ZYZ这样的运动,首先这玩意不能转四元数,因此只能用三个旋转矩阵来计算,而这种情况下,还是要面临万向节死锁!
因此,实际上万向节死锁是无法完全消灭的,总要去面对它。
更多内容可见我关于万向节死锁的文章。
switch (order) {
case 'XYZ':
this._x = s1 * c2 * c3 + c1 * s2 * s3;
this._y = c1 * s2 * c3 - s1 * c2 * s3;
this._z = c1 * c2 * s3 + s1 * s2 * c3;
this._w = c1 * c2 * c3 - s1 * s2 * s3;
break;
case 'YXZ':
this._x = s1 * c2 * c3 + c1 * s2 * s3;
this._y = c1 * s2 * c3 - s1 * c2 * s3;
this._z = c1 * c2 * s3 - s1 * s2 * c3;
this._w = c1 * c2 * c3 + s1 * s2 * s3;
break:
case 'ZXY':
this._x = s1 * c2 * c3 - c1 * s2 * s3;
this._y = c1 * s2 * c3 + s1 * c2 * s3;
this._z = c1 * c2 * s3 + s1 * s2 * c3;
this._w = c1 * c2 * c3 - s1 * s2 * s3;
break;
case 'ZYX':
this._x = s1 * c2 * c3 - c1 * s2 * s3;
this._y = c1 * s2 * c3 + s1 * c2 * s3;
this._z = c1 * c2 * s3 - s1 * s2 * c3;
this._w = c1 * c2 * c3 + s1 * s2 * s3;
break;
case 'YZX':
this._x = s1 * c2 * c3 + c1 * s2 * s3;
this._y = c1 * s2 * c3 + s1 * c2 * s3;
this._z = c1 * c2 * s3 - s1 * s2 * c3;
this._w = c1 * c2 * c3 - s1 * s2 * s3;
break;
case 'XZY':
this._x = s1 * c2 * c3 - c1 * s2 * s3;
this._y = c1 * s2 * c3 - s1 * c2 * s3;
this._z = c1 * c2 * s3 + s1 * s2 * c3;
this._w = c1 * c2 * c3 + s1 * s2 * s3;
break;
default:
console.warn('THREE.Quaternion: .setFromEuler() encountered an unknown order: ' + order);
}
2.2.6 3x3矩阵与4x4矩阵(涵盖多种变换)
(对比:除了平移之外,3x3矩阵可表示其余任意一种变换,也可将多组变换通过乘法进行拼接,但受限于矩阵运算的方法,3x3矩阵不能表示平移,具体分析可看《游戏引擎架构》Jason Gregory的第四章,而4x4矩阵理论上可表示任意一种变换,包括平移,旋转,缩放及/或切变,一组变换串接成的某目标变换的4x4矩阵称为仿射矩阵,且任何一个仿射矩阵均可由一组表示纯平移,纯旋转,纯缩放及/或切变,通过乘法串接形成,因此,虽然一个仿射矩阵很难直接想象出来,但拆分为基础变换的组合相对简单。由于相比3x3矩阵而言,4x4矩阵可表示任意一种(包括平移)的变换,因此在游戏开发中,4x4矩阵通常更为常用,但在无位移的情况下,也因情况而定。)
补充:具体是矩阵x向量,还是向量x矩阵,这个顺序是按照矩阵由列还是行向量组成而定的,一般常用的是由列向量组成矩阵,也即向量在矩阵的右侧,但如果某引擎核心是基于行向量,则基础变换矩阵的写法也应有所调整,在threejs库中是基于列向量的。
此外,最先接触向量的最先变换,而在threejs内,向量在矩阵的右边,因此,变换A,变换B,变换C的乘法顺序,应该是CBA*向量。
综上所述,与基于角度的旋转不同,矩阵既可以表示旋转,也可以表示平移,缩放,切变等,且可以通过一个个基础变换,通过乘法拼接而成,Vector3给定了基于3x3矩阵或基于4x4矩阵的变换方法,也即,可以首先通过串连计算出仿射矩阵或3x3变换矩阵,再通过调用方法applyMatrix3或applyMatrix4,将其应用于向量上做某种变换。
接下来看下3x3矩阵(applyMatrix3)的源码,这里传参是三维矩阵类,先放下官方文档关于这个类的地址threejs文档中的Matrix3类,后面有空再写篇文章读下源码。
elements是三维矩阵中的元素,是一个Array数组,这里是按照列优先的顺序来储存的,通过读源码可知,函数意为给点在左边乘以一个3x3的线性变换矩阵,且矩阵由列向量组成。
_proto.applyMatrix3 = function applyMatrix3(m) {
var x = this.x, y = this.y, z = this.z;
var e = m.elements;
this.x = e[0] * x + e[3] * y + e[6] * z;
this.y = e[1] * x + e[4] * y + e[7] * z;
this.z = e[2] * x + e[5] * y + e[8] * z;
return this;
};
4x4矩阵也是一样的,只不过由于调用该方法的this是一个3维向量,因此在计算时需要临时添加第4个维度w,在运算后,再将4维坐标转3维,下面是《游戏引擎架构》里关于4维坐标转3维的方法,这个转换过程被隐藏在applyMatrix4内部了

_proto.applyMatrix4 = function applyMatrix4(m) {
var x = this.x,
y = this.y,
z = this.z;
var e = m.elements;
var w = 1 / (e[3] * x + e[7] * y + e[11] * z + e[15]);
this.x = (e[0] * x + e[4] * y + e[8] * z + e[12]) * w;
this.y = (e[1] * x + e[5] * y + e[9] * z + e[13]) * w;
this.z = (e[2] * x + e[6] * y + e[10] * z + e[14]) * w;
return this;
};
为了便于理解,这里把applyMatrix4矩阵与向量相乘的表达式贴在下面,可以看到,为了与4x4矩阵相乘,右边向量需要加一个维度w,且w值为1(其实这里有两种w的设置方法,一种是w设为1,另一种是设为0,若右边所乘为纯方向向量,则这里要把w设置为0,但applyMatrix4方法内是设置为1的,也即applyMatrix4方法所处理的三维向量为包括方向与长度的向量,而不是纯方向向量),在源码中计算的var w,实际上就是上面图片所示,将计算后的4位点转换为3维点时,除以w的一个操作,源码中是乘,因为计算w时已经被1所除了。

2.3 基于某种方式设置向量属性(xyz值)
2.3.1 基于笛卡尔坐标系设置xyz值
| 方法 | 用途 |
|---|---|
| .set ( x : Float, y : Float, z : Float ) : this | 设置该向量的x、y 和 z 分量。 |
| .setX ( x : Float ) : this | 将向量中的x值替换为x。 |
| .setY ( y : Float ) : this | 将向量中的y值替换为y。 |
| .setZ ( z : Float ) : this | 将向量中的z值替换为z。 |
| .setComponent ( index : Integer, value : Float ) : null | 若index为 0 则设置 x 值为 value。若index为 1 则设置 y 值为 value。若index为 2 则设置 z 值为 value。 |
| .setScalar ( scalar : Float ) : this | 将该向量的x、y和z值同时设置为等于传入的scalar。 |
看下源码,理解上应该没有难度,不多赘述。
_proto.set = function set(x, y, z) {
if (z === undefined) z = this.z; // sprite.scale.set(x,y)
this.x = x;
this.y = y;
this.z = z;
return this;
};
_proto.setX = function setX(x) {
this.x = x;
return this;
};
_proto.setY = function setY(y) {
this.y = y;
return this;
};
_proto.setZ = function setZ(z) {
this.z = z;
return this;
};
_proto.setScalar = function setScalar(scalar) {
this.x = scalar;
this.y = scalar;
this.z = scalar;
return this;
};
2.3.2 基于圆柱或球坐标系设置xyz值
| 方法 | 用途 |
|---|---|
| .setFromCylindrical ( c : Cylindrical ) : this | 从圆柱坐标c中设置该向量。 |
| .setFromCylindricalCoords ( radius : Float, theta : Float, y : Float ) : this | 从圆柱坐标中的radius、theta和y设置该向量。 |
| .setFromSpherical ( s : Spherical ) : this | 从球坐标s中设置该向量。 |
| .setFromSphericalCoords ( radius : Float, phi : Float, theta : Float ) : this | 从球坐标中的radius、phi和theta设置该向量。 |
在2.3.1中介绍了基于直角笛卡尔坐标系直接修改向量xyz值的方法,在这一节中,将额外拓展两个新的坐标系,即基于圆柱,与球坐标系来修改点的xyz值。下面贴下《游戏引擎架构》中关于这两种常用坐标系的讲解:

了解圆柱与球坐标系如何表示一个点后,下面看setFromCylindrical和setFromCylindricalCoords 的源码(基于圆柱坐标系):
_proto.setFromCylindrical = function setFromCylindrical(c) {
return this.setFromCylindricalCoords(c.radius, c.theta, c.y);
};
_proto.setFromCylindricalCoords = function setFromCylindricalCoords(radius, theta, y) {
this.x = radius * Math.sin(theta);
this.y = y;
this.z = radius * Math.cos(theta);
return this;
};
这两个方法的区别是,setFromCylindrical基于圆柱坐标系类所创造的点来修改向量的xyz值,而setFromCylindricalCoords是通过直接指明圆柱坐标系下某点的三个值,来修改向量的xyz值,实际上,通过代码也可看出,两者是一个意思。
但是建议使用setFromCylindrical方法,因为通过Cylindrical(圆柱坐标)类来构建的点,会有一些好用的方法,例如将xyz点转为圆柱坐标系下的点等等。
下面看下setFromSpherical 与setFromSphericalCoords (球坐标系)的源码:
这俩方法跟上面圆柱坐标系的两种方法差不多,都是一个基于值,一个基于类,同样建议使用基于类的方法(当然,如果考虑到占用空间的问题,在确实没必要的情况下,使用基于值也是完全可以的,两种方法本质上并无区别)。
_proto.setFromSpherical = function setFromSpherical(s) {
return this.setFromSphericalCoords(s.radius, s.phi, s.theta);
};
_proto.setFromSphericalCoords = function setFromSphericalCoords(radius, phi, theta) {
var sinPhiRadius = Math.sin(phi) * radius;
this.x = sinPhiRadius * Math.sin(theta);
this.y = Math.cos(phi) * radius;
this.z = sinPhiRadius * Math.cos(theta);
return this;
};
补充:三种坐标系各有利弊,其实作用都是为了将一个向量(点)移动到另一个位置,其中,圆柱与球坐标系,适合控制点沿着曲线运动,例如,通过调整圆柱坐标系中点的角度与y值,可使一点呈螺旋状逐渐上升或下降,而调整球面坐标系中垂直于xz平面的角度,可使点做类似太阳东升西落的运动,而这些“圆弧”运动,用笛卡尔坐标系是很难控制的。
因此,在不同场景下,选用合适的坐标系是很有价值的。
2.3.3 基于矩阵设置xyz值
| 方法 | 用途 |
|---|---|
| .setFromMatrixColumn ( matrix : Matrix4, index : Integer ) : this | 从传入的四阶矩阵matrix由index指定的列中, 设置该向量的x值、y值和z值。 |
| .setFromMatrix3Column ( matrix : Matrix3, index : Integer ) : this | 从matrix的索引列 设置此向量的x,y和z分量。 |
| .setFromMatrixPosition ( m : Matrix4 ) : this | 从变换矩阵(transformation matrix)m中, 设置该向量为其中与位置相关的元素。 |
| .setFromMatrixScale ( m : Matrix4 ) : this | 从变换矩阵(transformation matrix)m中, 设置该向量为其中与缩放相关的元素。 |
接下来看下setFromMatrixPosition 的源码,即基于4x4矩阵中与位移相关数值来设置点的xyz值,传入参数是一个4x4矩阵。
_proto.setFromMatrixPosition = function setFromMatrixPosition(m) {
var e = m.elements;
this.x = e[12];
this.y = e[13];
this.z = e[14];
return this;
};
先讲下何为“矩阵中与位移相关的值”,如下图示。下面展示了两种不同的变换矩阵作用于点的方法,上面是点乘矩阵,下面是矩阵乘点,在部分引擎中使用的是上面的规则,而在threejs中,则是使用下面的规则。(补充:如果矩阵由列向量组成,则应使用矩阵乘点,如果矩阵由行向量组成,则应使用点乘矩阵,如不理解也不碍事,会用即可)

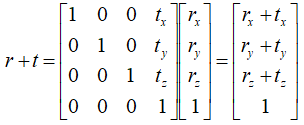
通过给向量与矩阵加一个维度,可以让矩阵也具有使点平移的功能,而与平移有关的数值,根据不同的相乘顺序,在4x4矩阵上的位置也不同,(补充一句,3x3矩阵无法进行平移,只有4x4矩阵里有平移),观察图片可知,在threejs的规则中,平移的3个数值在4x4矩阵的右侧。
该方法的大概作用可以描述为,仅取某仿射矩阵中的平移效果,而不作其他变换,例如一个矩阵可使模型旋转,放大后按某向量进行平移,则使用该方法可消除其他效果而仅作平移。
接下来看下setFromMatrixColumn的源码,其中fromArray仅看源码(它也是Vector3的方法,会在其他小节讲到),可知其本意是从一个数组中某个位置开始连续的取得3个数值,并将三个数值作为xyz值赋值给调用它的Vector3向量。
但是,fromArray在此处的用处,是从一个矩阵中取得一列的前3个维度的值(因为threejs所基于的矩阵均由列向量组成,因此,setFromMatrixColumn函数的含义是将某矩阵中某列所表示的那个向量作用于this向量),取前3个维度,因为组成4x4矩阵的列向量的第4个维度w,并不需要(也无法)作用于只有xyz三个维度的Vector3向量。
因此,简单来说就是,setFromMatrixColumn的作用是,从一个4x4矩阵中,按照index指示的列号,取得该列的前3个维度值,并将其分别赋值给this的xyz值。
_proto.setFromMatrixColumn = function setFromMatrixColumn(m, index) {
return this.fromArray(m.elements, index * 4);
};
下面看下setFromMatrix3Column 的源码,它其实就是setFromMatrixColumn 方法的3x3矩阵版
_proto.setFromMatrix3Column = function setFromMatrix3Column(m, index) {
return this.fromArray(m.elements, index * 3);
};
这里再来回顾下threejs中储存4x4矩阵元素时,各个元素在数组中的下标,如下图,矩阵中第二行第三个元素,在实际储存的elements数组中为e(9),即储存在下标为9的位置。

以及threejs中储存3x3矩阵元素时,各个元素在数组中的下标,如下图。

因此,举例, this.setFromMatrixColumn(m, 0)的意思是,从e(0)开始,取得e(0)赋值给this.x,取得e(1)赋值给this.y,以及取得e(2)赋值给this.z,而setFromMatrixColumn(m, 1)的意思是,从e(4)开始,取得e(4)赋值给this.x,取得e(5)赋值给this.y,以及取得e(6)赋值给this.z,以此类推,这也是为什么index 要乘以4的原因。(3x3矩阵不再赘述,跟4x4是一个道理。)
接下来看下setFromMatrixScale 的源码,其中length()为获得向量的模,也就是原点到向量点的线段长度。
_proto.setFromMatrixScale = function setFromMatrixScale(m) {
var sx = this.setFromMatrixColumn(m, 0).length();
var sy = this.setFromMatrixColumn(m, 1).length();
var sz = this.setFromMatrixColumn(m, 2).length();
this.x = sx;
this.y = sy;
this.z = sz;
return this;
};
setFromMatrixScale 所传入的参数是一个4x4矩阵,this.setFromMatrixColumn(m, 0).length()意为,在将4x4矩阵m的某一列所表示的向量赋值给this后,计算新生成的向量this的模长。分析至此,setFromMatrixScale方法的含义也很好理解了,它会将传入的4x4矩阵中,前3列且前3维度的向量提取出来,分别计算模长后,赋值给this的x,y,z值,也即,提取出缩放相关的数值,并将其赋值给向量。
补充:纯缩放矩阵如下图所示,如果传入setFromMatrixColumn的矩阵为这样的纯缩放矩阵,则提取出的this向量,与另一向量做“乘法”运算(multiply方法)等价于将该纯缩放矩阵作用于另一向量。

2.3.4 在原向量方向的基础上改变向量长度
| 方法 | 用途 |
|---|---|
| .setLength ( l : Float ) : this | 将该向量的方向设置为和原向量相同,但是长度(length)为l。 |
看下setLength 源码
_proto.setLength = function setLength(length) {
return this.normalize().multiplyScalar(length);
};
【明天再说我先睡了】
3、方法的应用场景分析
缩放矩阵:如果各个维度缩放尺度不一样,则会形变,因此通常对模型仅使用尺度一致的缩放矩阵,这种三个轴缩放因子相等的情况,叫统一缩放。
【待续…】
【备注下要写啥:】
可视化一下各个变换作用在模型上的效果