a星算法的优缺点_A星寻路算法
本节主要讲述A星寻路算法,下面通过一个经典案例开始。
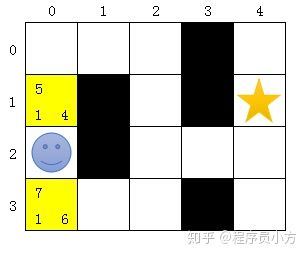
案例:在下面的图片中,小人想要找到五角星,主要有2条路径,一条是蓝色部分,从上面开始寻找,此时总步数为9步;另外一种就是从下面开始寻找,此时总步数为7步,我们通过步数得出,最短路径的步数为7步,怎么通过代码实现搜索步数呢,下面我们开始。
A星寻路法主要是为每个节点定义一下几个内容,通过公式计算得出最短路径的步数以及打印最短路径。
1、父节点:保存每个节点对应的父节点,在我们找到目标节点时,可以通过父节点寻找每个节点的位置,从而打印出节点路径。
2、已使用步数:从开始节点到当前节点已使用的步数,每个节点一步
3、无障碍距离 :当前节点到目标节点无视障碍的距离,等于行坐标距离+列坐标距离
4、期望完成步数:已使用步数+无障碍的步数,搜索最短步数时的依据。
5、节点的行、列坐标,标识当前节点所在的位置。
为了方便看图,每个节点左上角表示期望完成步数,左下角表示已使用步数,右下角表示无障碍距离。
class Node{
/** 行坐标 **/
int x;
/** 列坐标 **/
int y;
/** 已使用步数 :从开始节点到当前节点已使用的步数**/
int usedSteps;
/** 无障碍距离 :当前节点到目标节点无视障碍的距离**/
int distance;
/** 期望步数 = 已使用步数+无障碍距离**/
int expectedSteps;
/** 父节点:打印路径时需要 **/
Node parent;
}下面开始对案例的详细步骤解答:
首先我们定义一个迷宫:
/** 迷宫 1表示障碍物 **/
public static int[][] MAZE = {
{
0, 0, 0, 1, 0 },
{
0, 1, 0, 1, 0 },
{
0, 1, 0, 0, 0 },
{
0, 0, 0, 1, 0 }
};我们需要建立2个list,用以保存那些节点已经被访问过,那些节点准备访问。
/** 待访问的节点 **/
ArrayList readyList = new ArrayList<>();
/** 已访问的节点 **/
ArrayList visitedList = new ArrayList<>(); 我们计算开始节点周围节点已使用步数、无障碍距离、期望完成步数,并将结果放到待访问节点列表中。由于每个节点都有上下左右4个方向,为了避免写4次,我们用一个数组表示方向。
/** 定义上下左右方向 **/
static int[][] stepArray = {
{
0, 1 }, {
0, -1 }, {
1, 0 }, {
-1, 0 } };
/**
* 找到指定节点周围所有的可访问节点
* 数组越界判断、障碍物判断、已访问列表判断
* @param min
* @return 如果未找到,返回空对象
*/
private static ArrayList findNeighbour(Node node);
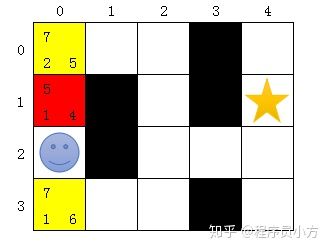
开始节点由于已访问,将开始节点放到已访问列表中。由于刚开始访问,已使用步数都是1,父节点都是开始节点。上面黄色节点到终点的距离为4,下面的为6。
计算公式:Math.abs(x-end.x)+Math.abs(y-end.y);
黄色:待访问 红色:已访问此时我们待访问节点已经有2个节点了(1,0)和(3,0),已访问节点有1个(2,0),我们查找待访问节点里面期望步数最小的一个,将访问该节点,并将该节点保存到已访问节点。
/**
* 获取list中期望步数最小的节点
*
* @param nodes
* @return
*/
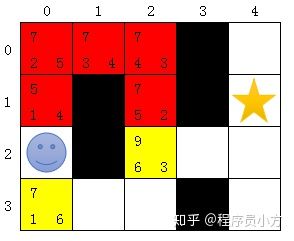
public static Node getMinNode(ArrayList nodes) ; 从图得知,上面一个黄色节点期望步数为5,我们获取这个节点,然后将周围的节点保存到待访问列表中(需要在已访问列表中查询是否存在,存在则不保存)。此节点步数在父节点的基础上+1,无障碍距离为5,计算期望步数为7。
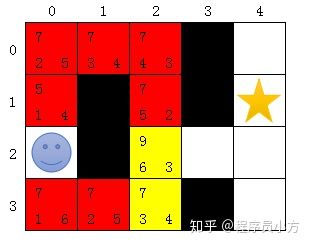
黄色:待访问 红色:已访问重复以上步骤,待访问列表中获取期望值最小值,此时黄色待访问部分2个节点期望步数相等,根据不同算法随机获取一个,假设我们这边获取的是上面的节点(0,0),保存到已访问列表,并将周围的未访问节点不重复的保存到待访问节点。
黄色:待访问 红色:已访问继续循环,假设一直获取到上面的黄色节点,最终到达以下情况。
黄色:待访问 红色:已访问此时上面的黄色节点最大期步数7,开始处理下面的节点。
黄色:待访问 红色:已访问此时我们处理黄色期望步数为7的时候,发现左边节点已访问,右边和下边不可访问,上面的已经在待访问清单里面了,由于待访问清单里面不能重复放入节点,此时我们有2个选择,上面的节点的父节点要么是(1,2),要么是(3,2),该如何选择呢?
仔细分析发现,如果选择父节点为(1,2),那么我们的期望步数 9= 6 + 3 ,而如果我们选择父节点为(3,2),我们期望步数 7= 4 + 3,毫不犹豫,我们选择期望步数少的。
黄色:待访问 红色:已访问继续访问。
黄色:待访问 红色:已访问访问到此时,我们访问黄色节点,然后寻找周围节点,找到星星节点,计算时发现无障碍距离等于0,OK,终于找到目标节点,对目标节点的父节点赋值,寻路结束。下面拿到该节点,根据父节点一直向上找,找到所有路径,打印出路径,就大功告成了。
具体代码如下:
/**
* A星算法,寻找2点之间的最短路径
*/
public class AStarSearch {
/** 迷宫 1表示障碍物 **/
public static int[][] MAZE = {
{
0, 0, 0, 1, 0 },
{
0, 1, 0, 1, 0 },
{
0, 1, 0, 0, 0 },
{
0, 0, 0, 1, 0 }
};
/** 待访问的节点 **/
static ArrayList readyList = new ArrayList<>();
/** 已访问的节点 **/
static ArrayList visitedList = new ArrayList<>();
/** 定义上下左右方向 **/
static int[][] stepArray = {
{
0, 1 }, {
0, -1 }, {
1, 0 }, {
-1, 0 } };
/**
* A星寻路算法
*
* @param args
*/
public static Node aStarSearch(Node start, Node end) {
// 将起点存放到待访问节点
readyList.add(start);
while (readyList.size() > 0) {
// 获取待访问列表期望值最小的节点
Node min = getMinNode(readyList);
// 将该节点从readylist中移除,存放到visitedList列表中
readyList.remove(min);
visitedList.add(min);
// 找到最小节点周围所有的可访问节点
ArrayList list = findNeighbour(min);
for (Node node : list) {
// 计算所有节点的期望步数
node.initNode(min, end);
// 判断readylist是否存在同坐标节点
// 如果存在,则比较期望值,获取最小的一个,保存到readylist
// 如果不存在,则直接保存到readylist
Node tmp = findNode(readyList, node.x, node.y);
if (tmp == null) {
readyList.add(node);
}else if (node.expectedSteps < tmp.expectedSteps) {
readyList.remove(tmp);
readyList.add(node);
}
}
// 判断终点是否在列表中,如果在,则直接返回
Node tmp = findNode(readyList, end.x, end.y);
if (tmp != null) {
return tmp;
}
}
// 可访问节点列表为空,找不到路径,返回null
return null;
}
/**
* 找到指定节点周围所有的可访问节点
* 数组越界判断、障碍物判断、已访问列表判断
* @param min
* @return 如果未找到,返回空对象
*/
private static ArrayList findNeighbour(Node node) {
ArrayList resultList = new ArrayList<>();
// 获取上下左右4个节点的坐标并判断有效性
for (int i = 0; i < 4; i++) {
int x = node.x + stepArray[i][0];
int y = node.y + stepArray[i][1];
// 坐标越界判断
if (x < 0 || x >= MAZE.length || y < 0 || y >= MAZE[0].length) {
continue;
}
// 判断是否存在障碍物
if(MAZE[x][y] != 0){
continue;
}
// 判断是否在已访问节点
if (findNode(visitedList, x, y) != null) {
continue;
}
resultList.add(new Node(x, y));
}
return resultList;
}
/**
* 在指定的list中找寻对应坐标的节点
*
* @param list
* @param x
* @param y
* @return 查询无结果,返回null
*/
public static Node findNode(ArrayList list, int x, int y) {
if (list == null || list.size() == 0) {
return null;
}
// 根据坐标找寻节点
for (Node node : list) {
if (node.x == x && node.y == y) {
return node;
}
}
// 找不到,返回空
return null;
}
/**
* 获取list中期望步数最小的节点
*
* @param nodes
* @return
*/
public static Node getMinNode(ArrayList nodes) {
// 入参校验
if (nodes == null || nodes.size() == 0) {
return null;
} else if (nodes.size() == 1) {
return nodes.get(0);
}
// 获取期望值最小的节点
Node min = nodes.get(0);
for (Node node : nodes) {
if (node.expectedSteps < min.expectedSteps) {
min = node;
}
}
return min;
}
/**
* 打印从起点开始到当前节点的全路径
* 逆序保存到数组中,逆序开始打印
* @param node
*/
public static void print(Node node){
// 拷贝一份,防止参数被修改
Node end = node;
int i=0;
// 定义一个数组,逆序保存路径
int[][] array = new int[MAZE.length * MAZE[0].length][2];
array[i++] = new int[]{
end.x,end.y};
while(end.parent != null){
Node tmp = end.parent;
array[i++] = new int[]{
tmp.x,tmp.y};
end = tmp;
}
//循环数组,打印路径
for(i--;i>=0;i--){
System.out.println(Arrays.toString(array[i]));
}
}
public static void main(String[] args) {
/** 起点 **/
Node start = new Node(2, 0);
/** 终点 **/
Node end = new Node(1, 4);
Node node = aStarSearch(start, end);
if (node == null) {
System.out.println("终点不可达");
return;
}
print(node);
}
}
class Node {
/** 行坐标 **/
int x;
/** 列坐标 **/
int y;
/** 已使用步数 :从开始节点到当前节点已使用的步数 **/
int usedSteps;
/** 无障碍距离 :当前节点到目标节点无视障碍的距离 **/
int distance;
/** 期望步数 = 已使用步数+无障碍距离 **/
int expectedSteps;
/** 父节点:打印路径时需要 **/
Node parent;
/** 构造函数 **/
public Node(int x, int y) {
this.x = x;
this.y = y;
}
/**
* 根据父节点和目标节点,初始化已使用步数、无障碍距离、期望步数和父节点
*
* @param parent
* 父节点
* @param end
* 目标节点
*/
public void initNode(Node parent, Node end) {
this.parent = parent;
// 已使用步数 = 父节点已使用步数 + 1
if (parent == null) {
usedSteps = 1;
} else {
usedSteps = parent.usedSteps + 1;
}
// 无障碍距离 = 当前节点与目标节点的行坐标距离+列坐标距离
distance = Math.abs(x - end.x) + Math.abs(y - end.y);
// 期望完成步数 = 已使用步数 + 无障碍距离
expectedSteps = usedSteps + distance;
}
}