数据库关系代数详解
数据库关系代数
文章目录
- 数据库关系代数
-
- 1. 关系代数的运算
-
- 1.1 传统的关系运算
- 1.2 专门的关系运算
-
- 1.2.1 关系运算中的基础概念
- 1.2.2 元组的连接
- 1.2.3 象集(除法运算重要工具)
- 1.3 数学上的运算
-
- 1.3.1 并运算
- 1.3.2 差运算
- 1.3.3 交运算
- 1.3.4 笛卡尔积
- 1.4 关系运算
-
- 1.4.1 表格简介
- 1.4.2 选择(Selection)
-
- 1.4.2.1 选择查询(例1)
- 1.4.2.2 选择查询(例2)
- 1.4.2.3 选择查询(练习题)
- 1.4.3 投影(Projection)
-
- 1.4.3.1 投影查询(例1)
- 1.4.3.2 投影查询(例2)
- 1.4.4 连接(Join)
-
- 1.4.4.1 一般连接(例题)
- 1.4.4.2 等值连接
- 1.4.4.3 自然连接(特殊的等值连接)
- 1.4.4.4 外连接
- 1.4.5 除运算
1. 关系代数的运算
1.1 传统的关系运算
传统的关系运算起源于数学的集合论,有下面几种:
- 笛卡尔积运算
- 差运算
- 交运算
- 并运算
1.2 专门的关系运算
- 选择
- 投影
- 连接
- 除运算
1.2.1 关系运算中的基础概念
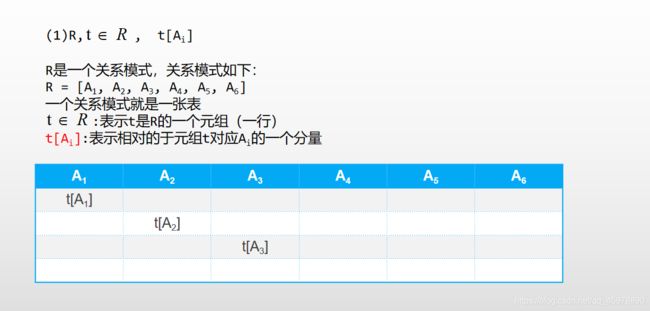
在学习关系代数的时候,我们脑海中要时刻拥有一张表格,还有一些表格的参数,这张表格如下:
比如说我们每个人都见过成绩单,牢记以下的比喻
-
R就为整张成绩单
-
R[A1, A2, A3,…Ai] = R[语文,英语,数学……学科]
-
t为某个同学 -
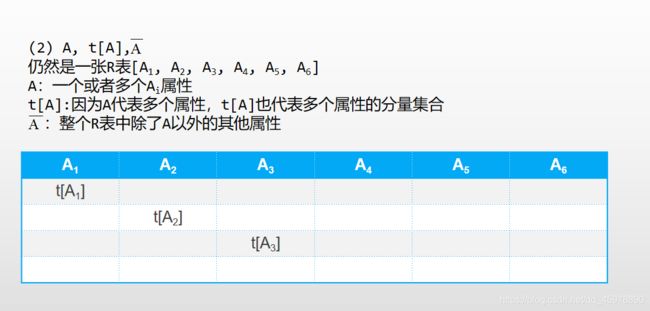
A不再是单独的一个属性,A可以代表一个或者多个属性 -
t[A]也不再是单独的某个属性分量,A代表多少个属性,t[A]就可以代表多少个属性分量
- 做一个比喻,
A再也不单独是某个学科,而是可以代表一科或者多科学科 t[A]也就不当作某个同学的一门成绩,而是可以当成某个同学的多门成绩,具体看A代表了多少学科A(头上一横……)就代表了全部的学科除了A代表的学科以外的学科
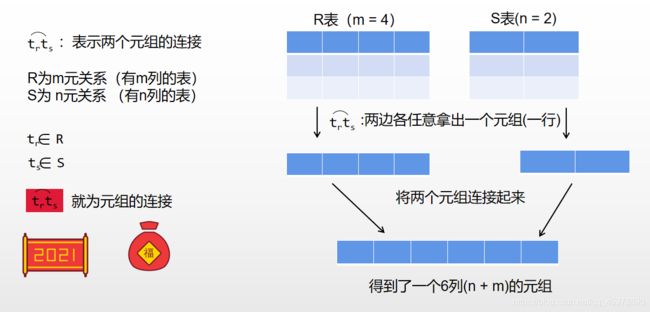
1.2.2 元组的连接
通过连接得到的这个元组,前m个分量是R表中的一个m元组,后n个分量是S表中的一个m元组
1.2.3 象集(除法运算重要工具)
给了我们一个关系R(X,Y),X和Y都代表了一个属性组,也就是X和Y都是属性的数量都是一列到多列
- 从上面的比喻来说,就是
X是成绩单一门课程的成绩或者多门课程成绩,Y也是一门成绩的课程或者多们成绩的课程 - 当
t[X] = x时:x在R中的象集为:Yx = {t[Y] | t 属于 R, t[X] = x} - 公式比较难懂,但是其实本身概念很简单
如下例:

X1在y属性分量上的象集就是全体X1对应的y上的属性分量组,也就是Y1,Y2,Y4
X2 在 y属性分量上的象集就是Y2
X4 在y属性分量上的象集就是Y3
1.3 数学上的运算
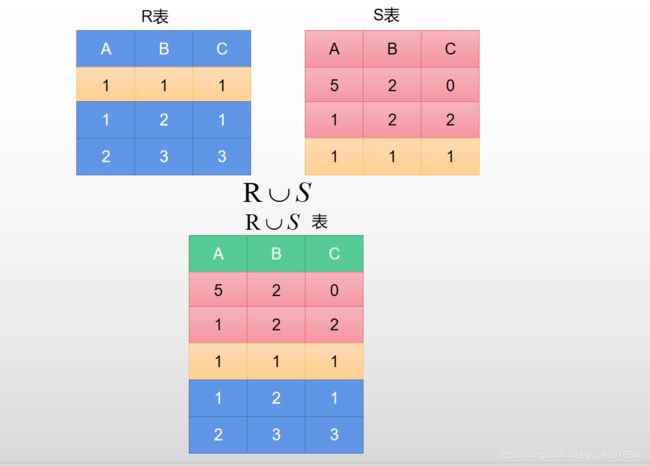
1.3.1 并运算
能够使用并运算的两个前提:
- 两张表格的元一样(两张表格列数一样)
- 相同的属性取自同一个域(属性都一样)
如图,在合并了之后呢,两个原始的表格和合并之后的新表格元数一样(列数一样),并且如果两个表之间有重复的,并运算会做去重处理,类似于集合的之间的并集
1.3.2 差运算
和并运算一样,差运算可以使用的前提
- 两个表格列数一样
- 两个表格的属性都相同
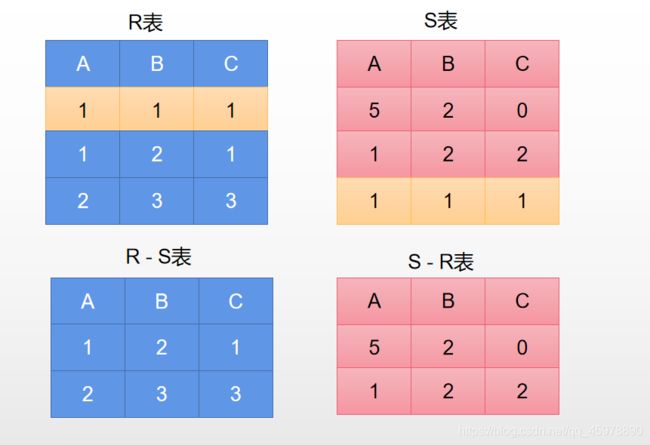
两个表进行了差运算之后,都仍然是n列
S-R表:S表中有任意一个元组和R表的一样,S表就去掉这个元组
R-S表:R表中有任意一个元组和S表的一样,R表就去掉这个元组
简言之:就是一张表,嫌弃另外一张表,我身上有那里和你一样,我改还不行嘛!
1.3.3 交运算
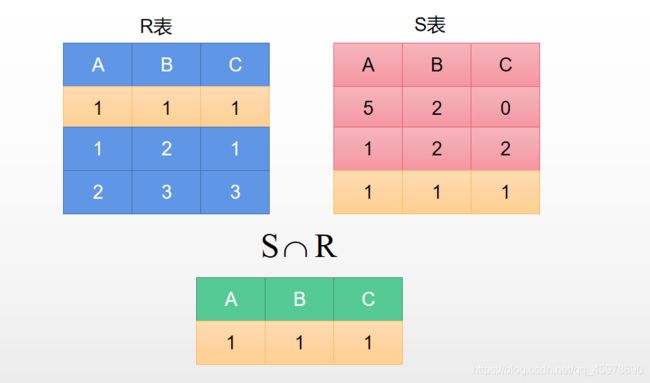
交运算能够使用的前提和前面两种运算一样
- 表格的列数相同
- 表格的属性都相同
两个表格进行并运算,就是把两个表格中一样的元素找出来,找出两张表格的共性
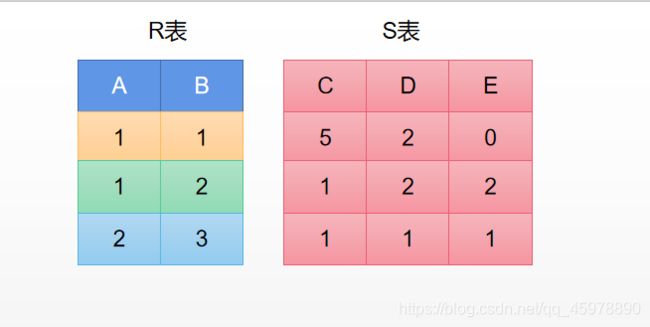
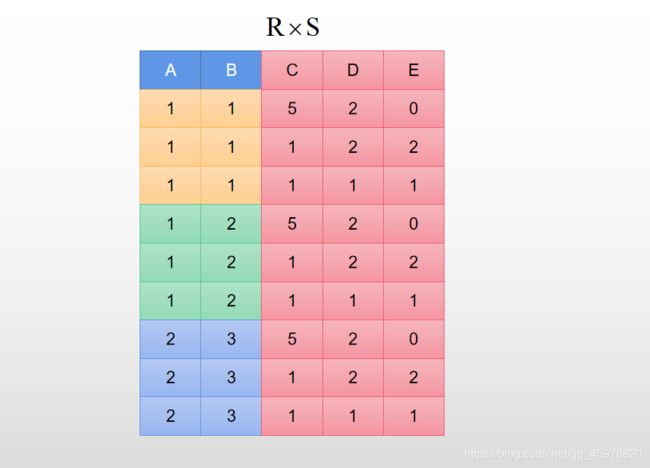
1.3.4 笛卡尔积
万能运算,没有任何限制。
R表:n元关系,k1个元组(k1行,n列)
S表:m元关系,k2个元组(k2行,m列)
R表和S表进行笛卡尔积
以上就是所有的数学关系代数运算
1.4 关系运算
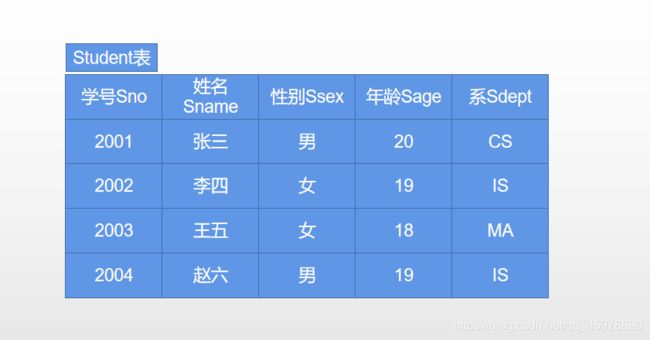
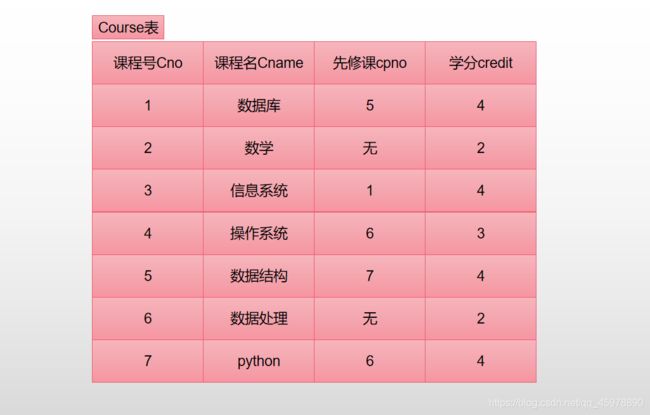
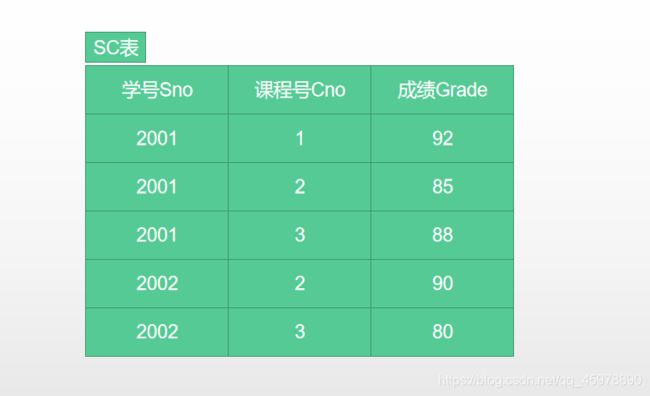
整个关系代数的学习需要使用学生课程选课数据库,需要熟悉以下表格
1.4.1 表格简介
1.4.2 选择(Selection)
- 选择也称之为限制
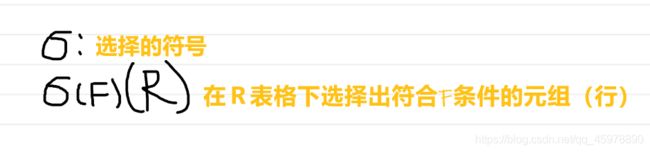
- 选择是针对的元组进行选择,选择出满足条件的元组
1.4.2.1 选择查询(例1)
查询全体信息系(IS)的学生
- 信息系在Student表格中有,所有我们的R表的位置是Student
Student表格的属性集合为{"Sno", "Sname", "Ssex", "Sage", "Sdept"}
- 我们需要的条件是
F(Sdept = IS)
1.4.2.2 选择查询(例2)
查询年龄小于20岁的学生
- 年龄在Student表格中存在,所以我们现需要查询的表格为Student表格
- 我们需要的条件是年龄小于20岁F(Sage < 20)
1.4.2.3 选择查询(练习题)
- 查询性别为女生的学生信息
- 查询学分等于四分的课程信息
- 查询CS系的学生信息
总结:选择运算是查询符合条件的行
1.4.3 投影(Projection)
我们可以看见,使用选择运算的时候,一行的所有全部信息我们都获取了,比如我查询了小于20岁的学生信息,我连学生的名字,学号,性别所有的信息都知道了,因为选择是选择出一行一行的结果,那么如果我只想知道小于20岁的学生名字,其他学号,学院等等的信息我都不想知道
这里就需要投影运算
选择运算是针对属性进行选择的运算,也就是投影是选择出符合条件的一列,并且会自动取消某些行(后面会举例说明)

1.4.3.1 投影查询(例1)
查询学生的姓名和学生的系,从需要查询的这个条件可以看出来我们需要查询的是姓名列和学生所在系列
- 学生的姓名和所在系在Student表格中,所以我们需要在Student表格中进行查询
- 需要查询的属性为学生的姓名和学生的系
题目的答案为:
Sname 和 Sdept之间用逗号分隔
1.4.3.2 投影查询(例2)
查询学生表Student中有那些系
- 首先,我们需要在Student表中进行查询
- 我们需要查询的属性为系
题目答案为:

可是我们最终查询出来的答案应该是什么样子的呢?
总结:投影查询得到的是一列
1.4.4 连接(Join)
连接的含义:从两个关系的笛卡尔积中选择属性之间满足一定关系的元组
解释:就是在两张表的笛卡尔积后得到的那张大表中再次选取一些符合我们条件的元组
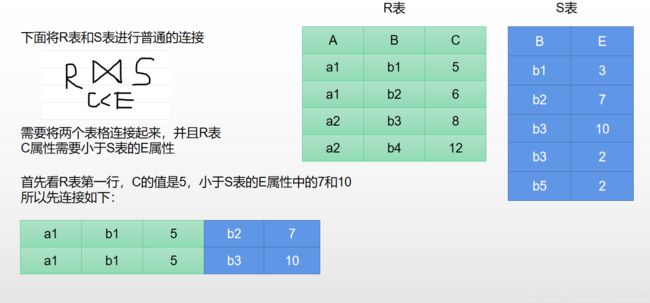
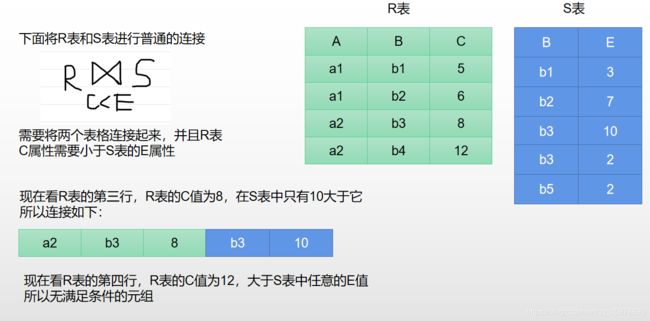
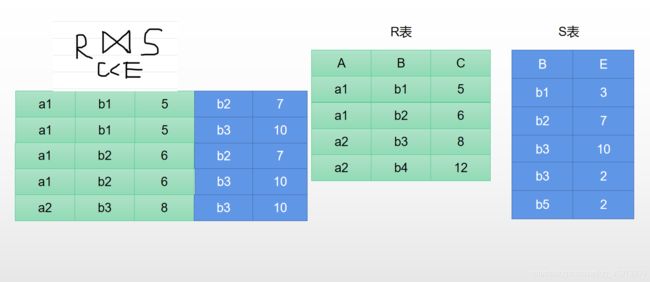
1.4.4.1 一般连接(例题)
一般连接就是条件连接,需要将两个表格按照条件连接起来
第一步:
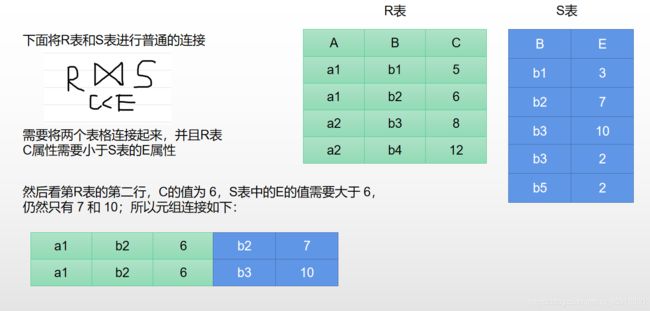
第二步:
第三步:
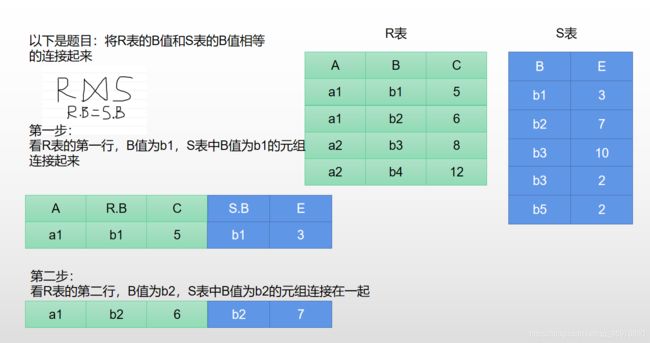
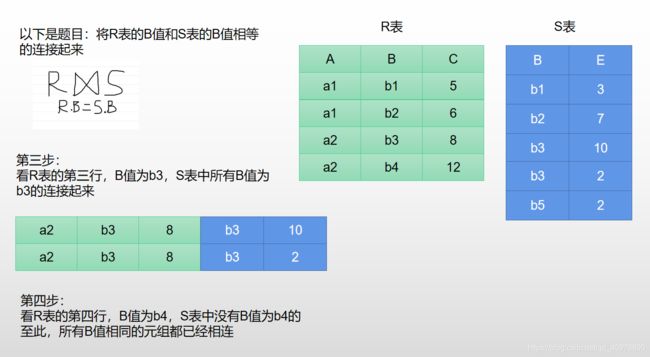
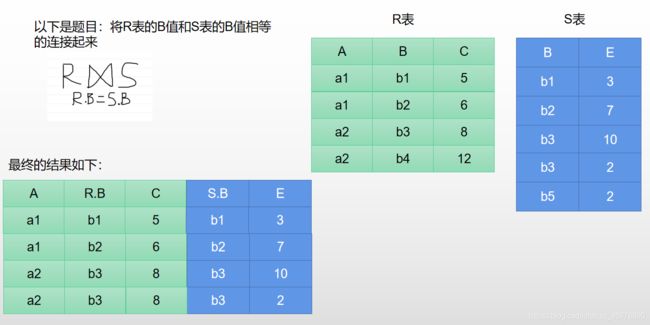
1.4.4.2 等值连接
等值连接是一种特殊的一般连接
- 两个表需要有相同的属性列
下面通过具体的题目来进行了解
第三步:
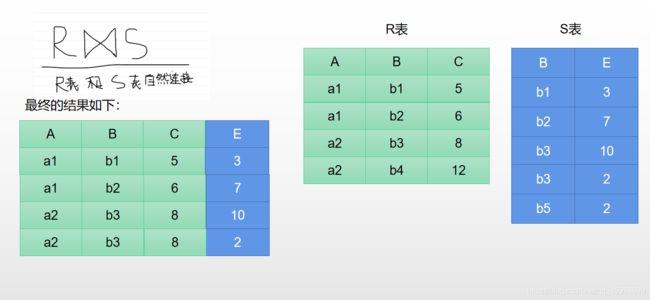
1.4.4.3 自然连接(特殊的等值连接)
自然连接是一种特殊的等值连接,也是相等的相连,但是我们发现了等值连接的时候,因为R.B和S.B是相等的,所以R.B和S.B就重复了,如上图中最后结果的第二列的R.B和S.B,因为重复造成额外的空间浪费。所以自然连接就是用来解决这个问题的
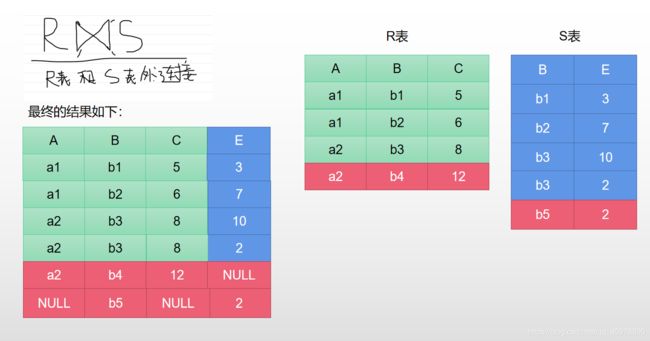
1.4.4.4 外连接
我们从自然连接中又发现了一个问题,如下图:
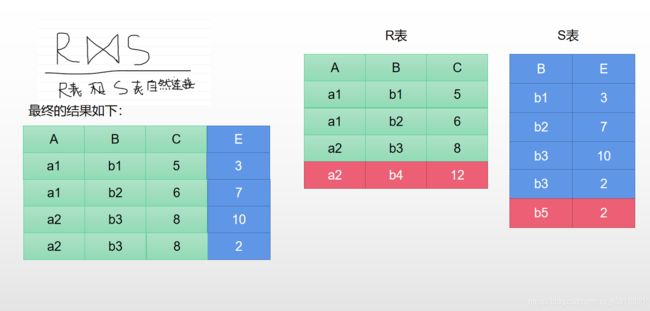
就是图中标记为红色的地方,因为不符合我们的条件在自然连接和等值连接的时候都会被丢弃,这种连接叫做内连接,而与内连接相反的就叫外连接
-
左外连接:因为R表在左边,所以最终的结果只保留R表中被丢弃的,S表的仍然丢弃
-
右外连接:因为S表在右边,所以最终的结果只保留S表中被丢弃的,R表的仍然丢弃
1.4.5 除运算
一些学习上的感悟:除运算在关系代数中是一个十分强大的工具,但是除法运算的定义看起来十分的晦涩难懂,可定义又是十分重要的,相信很多人在看教科书的过程中,每次看定义这块的时候都会很懵,然后看了例子之后就会理解定义的意思,但是懂了定义的大意之后很少就会有人再回头去理解定义,例子固然是用来让我们可以清晰的理解定义的大意的,但是我们通过例子理解定义的大意之后,我们仍然要回归定义,只有这样我们才能学得深入(个人对于学习上的一些理解,欢迎一起交流)
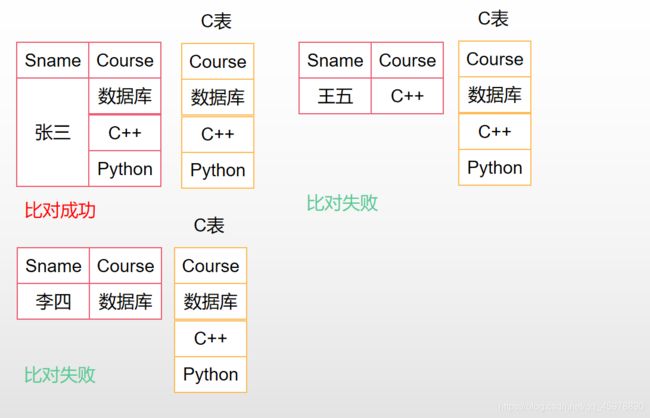
现在我们有一个问题,就是我们想要找出学习最积极的那位学生,也就是选修了所有课程的那个学生,先暂时放弃除法运算,以我们最朴素的情感,用自己的逻辑来解决这道题目,按照自己的想法,就像设计一个程序一样,需要几步做出这个问题
以下是按照我自己的想法:
实际上,我们的除法运算就是这个逻辑,但是除法运算的更为严谨,以下是除法运算的的步骤(SC ÷ C),这里我们仍然采用我们上面使用的数据库,直接说结论(SC ➗ C)能找出答案
下面是简单的总结,当我们需要获取选取所有课程的学生的名单的时候
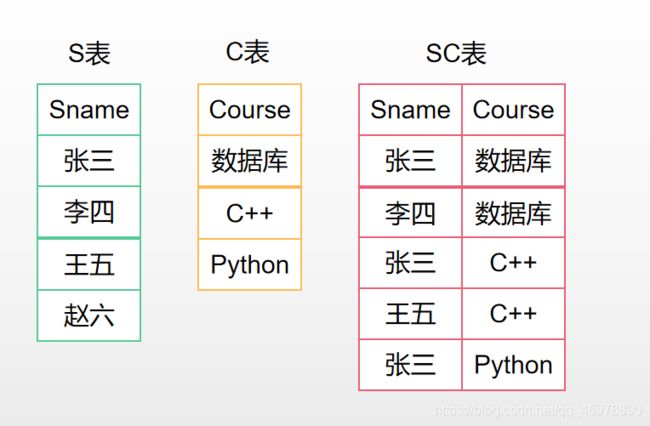
第一步:我们需要获取所有的课程到底是那些课程,所以我们对C表进行投影
第二步:我们需要获取选课的学生有那些,所以我们需要对SC表的S进行投影
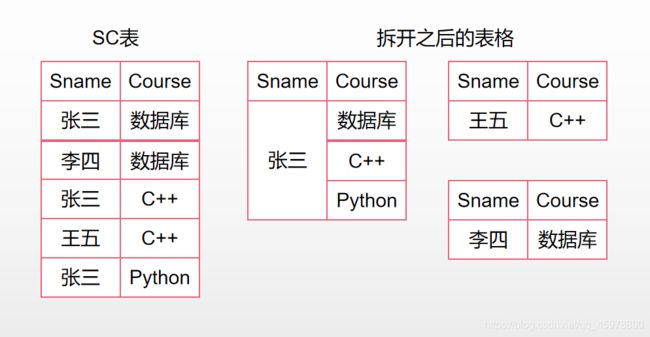
第三步:我们需要知道每个学生都选择哪些课程才能知道那个学生全选了课程,所以我们还需要的数据是SC表中,S的象集
第四步:也就是最后一步,我们需要进行比对,看看那个学生的象集包含了C表的投影
除法运算像一个函数,封装了以上的所有功能,我们调用这个函数的时候,把正确的参数放进去,就可以得到我们想要的答案
当我们看完结论再回头看定义,除法运算的定义如下:
多读几遍,我也想用自己的话把定义解释以下,但是如果不使用例子,把定义用自己的话解释一遍对于我来说太困难了……只可意会不可言传……如果使用例子无非把上面的例子再说一遍,这里使用其他博客的对于除法运算的总结:RS÷S的意义就是:“在R和S的联系RS中,找出与S中所有的元组有关系的R元组” 这篇博客地址为:关系代数除法运算
❤️完结撒花❤️