采用粒子群算法求解可靠性优化问题

1.问题描述：

 采用粒子群算法求解可靠性优化问题

2.部分程序：

 

clear;
clc;
close all

popsize=20;num=5;
jiage=[3,12,8,5,10];jiage=jiage';
kekaoxing=[0.96,0.93,0.85,0.8,0.75];r0=0.9;
bujian=zeros(popsize,num+2);                            %第num+1列放可靠性，num+2列放价格
newbujian=zeros(popsize,num+2);    
vol=zeros(popsize,num); 
% quanzhong=1;c1=1;c2=1;
c1=1.4962;c2=1.4962;
maxgen=100;

for i=1:popsize,
       for j=1:num,
            bujian(i,j)=ceil(5*rand);newbujian(i,j)=ceil(5*rand);
       end
       bujian(i,num+1)=1;newbujian(i,num+1)=1;
       for j=1:num,
                bujian(i,num+1)=bujian(i,num+1)*(1-(1-kekaoxing(j))^bujian(i,j));
                newbujian(i,num+1)=newbujian(i,num+1)*(1-(1-kekaoxing(j))^newbujian(i,j));
       end
       if bujian(i,num+1)        if newbujian(i,num+1)             bujian(i,num+2)=bujian(i,1:5)*jiage;
            newbujian(i,num+2)=newbujian(i,1:5)*jiage;
end

bestbujian=newbujian(1,:);

%%%%%%%%%%%%开始主循环%%%%%%%%%%%%
for k=1:maxgen,
    quanzhong=0.9-0.5*k/maxgen;
       %计算个体极值与全局极值
        for i=1:popsize,                                                        
                % %     bujian(i,num+2)=bujian(i,1:5)*jiaga;
                if bujian(i,num+2)                 if newbujian(i,num+2)         end
       track(k,1)=k;track(k,2)=bestbujian(num+2);track(k,3)=min(bujian(:,num+2));track(k,4)=max(bujian(:,num+2));
      %更新位置与速度  
        for i=1:popsize,
                for j=1:num,
                        vol(i,j)=quanzhong*vol(i,j)+c1*rand*(newbujian(i,j)-bujian(i,j))+c2*rand*(bestbujian(j)-bujian(i,j));      %更新速度       
                        bujian(i,j)=bujian(i,j)+vol(i,j);                           %更新位置
                        bujian(i,j)=ceil(bujian(i,j));
                        if(bujian(i,j)<0)   bujian(i,j)=0;   end
                end
        end
     % 计算可靠性，并保证可靠性的要求，同时计算价格
        for i=1:popsize,
                bujian(i,num+1)=1;
                                for j=1:num, bujian(i,num+1)=bujian(i,num+1)*(1-(1-kekaoxing(j))^bujian(i,j));end
                if bujian(i,num+1)                  bujian(i,num+2)=bujian(i,1:5)*jiage;
        end
end
%%%%%%%%%%%%结束主循环%%%%%%%%%%%%
bestbujian,
figure
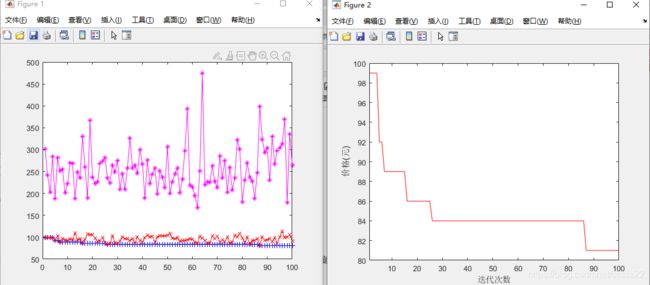
plot(track(:,1),track(:,2),'b-+',track(:,1),track(:,3),'r-x',track(:,1),track(:,4),'m-*');
t=max(track(:,2));
figure
plot(track(:,1),track(:,2),'r');
axis([1,maxgen,80,t+1]);
xlabel('迭代次数');ylabel('价格(元)');

3.仿真结论：

D00004