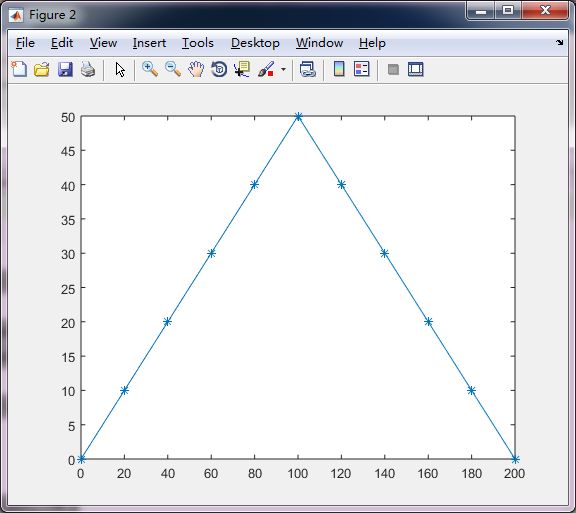
1. 问题描述
以如下的典型分段函数为例:
2. 技术背景
MATLAB。
3. 解决方案
以上的分段函数分别由两个函数构成:
- f1(x) = 0.5*x,当 x < 100;
- f2(x) = -0.5*x+100,当 x >= 100;
故整体的分段函数可以表示为:
f(x) = f1(x)(当 x < 100) + f2(x)(当 x >= 100)
如此,可以用一个统一的表达式表达,方便编程计算。
此处的(当 x < 100) 即为逻辑判断运算,如果满足条件为1,不满足条件为0.
4. 实施示例
— 逻辑判断运算
clc,clear
x0 = 0:20:200;
test1 = (x0 < 100)
test2 = (x0 >= 100)
运算结果如下:
test1 =
1 1 1 1 1 0 0 0 0 0 0
test2 =
0 0 0 0 0 1 1 1 1 1 1
- 构造分段函数,采用【匿名函数语法】
f = @(x) (x < 100).*(0.5*x) + (x >= 100).*(-0.5*x+100)
- 运算,绘图
f(x0)
figure
plot(x0,f(x0),'-*')
计算结果:
ans =
0 10 20 30 40 50 40 30 20 10 0
5. 常见问题
需要注意,代码中的乘法均为点乘:
.*
否则,对于向量数据,计算出现错误。
代码:
clc,clear
x0 = 0:20:200;
test1 = (x0 < 100)
test2 = (x0 >= 100)
f = @(x) (x < 100).*(0.5*x) + (x >= 100).*(-0.5*x+100)
f(x0)
figure
plot(x0,f(x0),'-*')