论文阅读-目标检测损失函数GIoU,DIoU,CIoU

目标检测损失函数GIoU,DIoU,CIoU

GIoU论文链接
DIoU和CIoU论文链接

1. GIoU

1.1. 问题提出

1.1.1. 范数损失的缺陷

在GIoU之前，主要是以IoU或者$l_{n}norm$作为损失函数的，而这些损失函数实际上是不够精细的。也就是说，即使观感上的差距很大，损失的值也会相同。以giou论文里举出的(a)图为例：

此时以$l_{2}norm$作为损失函数（也就是两对点之间的欧氏距离），为了简便起见，固定一个点不动（假设是左下角的点不动），以另一个点为圆心，做一个半径为r的圆，那么此时落在圆上的任意一点与固定点组成的bbox（黑色）和ground truth（绿色）之间的$l_{2}norm$损失值都是相同的（如a所示），在观感上，我们可能会趋向于最右侧的预测结果，但是在计算机使用$l_2$损失的时候是无法区分的。

1.1.2. IoU损失的缺陷

Iou只在bbox和gt之间有交集的时候才会生效，在他们没有交集的时候IoU始终为0，这样不能为反向传播时提供响应的梯度。例如下面的情况，IoU都为0，此时很难让网络进行调整。

1.2. 解决方案

针对IoU不能适应无交集的问题，提出了最小凸包的方案。
所谓的最小凸集就是恰好包含了gt和bbox的一个矩形，如下图所示，红色就是最小凸集。

而$$GIoU=IoU-\frac{C-(A\cup B)}{C}$$
在最小凸集的基础上，就解决了在gt与bbox无交集时梯度为0的问题。GIoU实际上就是在最小化这个最小凸集。

1.3 算法与代码

简单实现了以下原论文里的算法，原算法如下：

代码如下：

def getConvexShape(bbox_gt,bbox_pd):
    return [min(bbox_gt[0],bbox_pd[0]),min(bbox_gt[1],bbox_pd[1]),max(bbox_gt[2],bbox_pd[2]),max(bbox_gt[3],bbox_pd[3])]

def getBboxArea(bbox):
    if bbox[2] - bbox[0] > 0 and bbox[3]-bbox[1] > 0:
        return (bbox[2]-bbox[0]) * (bbox[3]-bbox[1])
    else:
        return 0.0

def getIntersection(bbox_gt,bbox_pd):
    return [max(bbox_gt[0],bbox_pd[0]),max(bbox_gt[1],bbox_pd[1]),min(bbox_gt[2],bbox_pd[2]),min(bbox_gt[3],bbox_pd[3])]

def getEnclosingBbox(bbox_cvx,bbox_gt):
    return [min(bbox_cvx[0],bbox_gt[0]),min(bbox_cvx[1],bbox_gt[1]),max(bbox_cvx[2],bbox_gt[2]),max(bbox_cvx[3],bbox_gt[3])] 

def getGIoU(bbox_gt,bbox_pd):
    #1. get bbox_hat
    bbox_cvx = getConvexShape(bbox_gt,bbox_pd)
    #2. caculate the area of ground truth
    area_bbox_gt = getBboxArea(bbox_gt)
    #3. caculate the area of bbox_hat
    area_bbox_cvx = getBboxArea(bbox_cvx)
    area_bbox_pd = getBboxArea(bbox_pd)
    #4. caculate the area of Intersection
    bbox_inter = getIntersection(bbox_gt,bbox_pd)
    area_bbox_inter = getBboxArea(bbox_inter)
    #5. Finding the coordinate of smallest enclosing box
    bbox_enclose = getEnclosingBbox(bbox_cvx,bbox_gt)
    #6. caculate the area of bbox_enclose
    area_bbox_enclose = getBboxArea(bbox_enclose)
    #7. caculate IoU
    #area_u = area_bbox_gt + area_bbox_cvx - area_bbox_inter # in paper
    #IoU = area_bbox_inter / area_u # in paper
    IoU = area_bbox_inter / ( area_bbox_gt + area_bbox_pd - area_bbox_inter )
    #8. caculate GIoU
    #GIoU = IoU - (( area_bbox_enclose - area_u ) / area_bbox_enclose) # in paper
    GIoU = IoU - ( ( area_bbox_cvx - area_bbox_gt - area_bbox_pd + area_bbox_inter ) / area_bbox_cvx )
    
    return IoU,GIoU

我不需要用到Loss，所以只是简单返回IoU，但是复现为原版的算法时出现了一些问题，以如下的bbox为例

bbox_gt = [5,5,10,10]
bbox_pd_1 = [0,0,3,3]
bbox_pd_2 = [0,0,1,1]

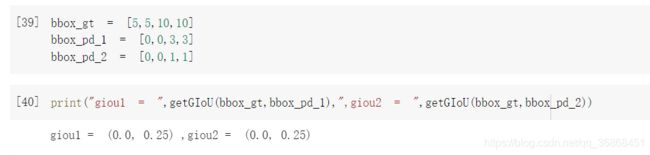
这似乎并不符合GIoU论文里的表述，这两者应当是不同的。在修正为现在的代码后解决了这样的问题。（不知道是我理解有问题还是算法有问题）

2. DIoU

2.1 问题提出

首先DIoU的作者观察到了GIoU收敛很慢以及GIoU本身也存在的一些问题。

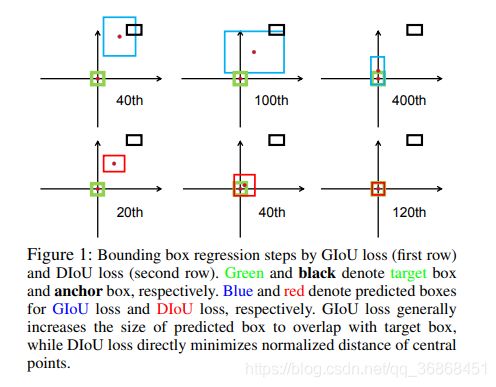
首先是收敛很慢的问题，如上图第一行所示，在迭代了400次之后的bbox依然距离gt有很大的差距。其次是GIoU在bbox是gt或者gt是bbox的时候会退化到IoU作为损失函数，此时在内部存在了相同的不能为模型提供梯度的问题（这里不是梯度为0，而是梯度相同，无法区分）。最后GIoU的收敛过程倾向于先让bbox变大，然后再进行IoU的迭代。

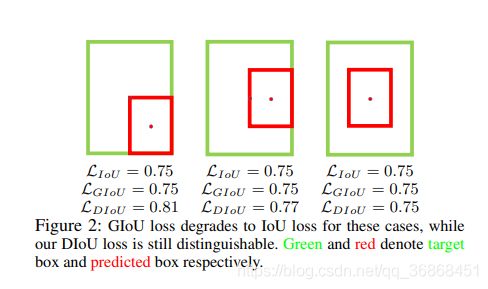
如上所示，显然第三个是我们观感上比较倾向的选择，但是计算机在使用IoU或者GIoU时是无法区分的。

2.2. 问题解决

那么针对这种问题，作者提出了将中心点作为考量的依据之一，并且总结出了一条好的损失函数应该考量的特性。

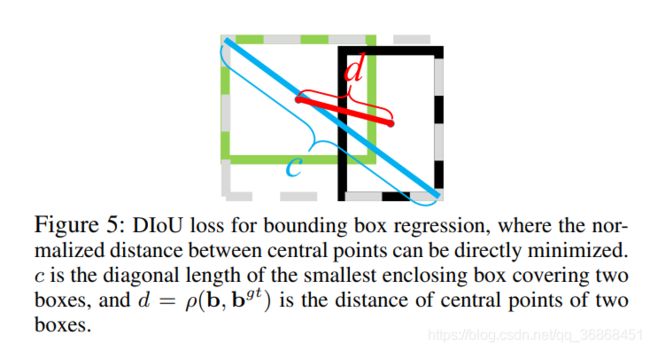
原作者提出了加入如下的惩罚项可以更快的收敛
$${\mathbf{R}}_{DIoU}=\frac{{\rho }^2(\mathbf{b},{\mathbf{b}}^{\mathbf{g}\mathbf{t}})}{c^2}$$
其中 ${\rho }^2(\mathbf{b},{\mathbf{b}}^{\mathbf{g}\mathbf{t}})$指的是bbox与gt中心点之间的距离，而c指的是最小凸集对角线的长度。
最终提出的DIoU损失函数如下：
$$L_{DIoU}=1-IoU+R_{DIoU}$$
在此基础上作者对这些损失函数进行了模拟实验的可视化，结果如下

2.3. 代码实现

仿照GIoU的算法，很容易就可以实现DIoU，最终代码如下（有部分函数用到了上面GIoU的函数）：

import math
def getCenterPoint(bbox):
    return (bbox[2]+bbox[0]) / 2. , (bbox[3]+bbox[1]) / 2.

def getDistance(point1,point2):
    return math.sqrt((point1[0]-point2[0]) ** 2 + (point1[1]-point2[1]) ** 2)

def getDIoU(bbox_gt,bbox_pd):
    #1. get bbox_hat
    bbox_cvx = getConvexShape(bbox_gt,bbox_pd)
    #2. caculate the area of ground truth
    area_bbox_gt = getBboxArea(bbox_gt)
    #3. caculate the area of predictions
    area_bbox_pd = getBboxArea(bbox_pd)
    #4. caculate the area of Intersection
    bbox_inter = getIntersection(bbox_gt,bbox_pd)
    area_bbox_inter = getBboxArea(bbox_inter)
    
    #5. caculate the center points
    center_point_gt = getCenterPoint(bbox_gt)
    center_point_pd = getCenterPoint(bbox_pd)

    #6. caculate the distance between the center point gt and the center point pd
    rho_2 = getDistance(center_point_gt, center_point_pd) ** 2

    #7. caculate the diag distance of cvx shape
    c_2 = getDistance(bbox_cvx[0:2], bbox_cvx[2:4]) ** 2

    #8. caculate IoU
    IoU = area_bbox_inter / ( area_bbox_gt + area_bbox_pd - area_bbox_inter )

    #9. get DIoU
    DIoU = IoU - rho_2 / c_2

    return IoU, DIoU

3. CIoU

在DIoU的基础上，为了让模型更快更好的收敛，原作者总结了三个目标检测损失函数应该考虑的因素，分别是overlap area, central point distance and aspect ratio。
基于此，作者提出了CIoU，也就是在DIoU的基础上增加了一个新的形状比例的惩罚项，如下：
$$R_{CIoU}=\alpha v$$
其中$$\alpha =\frac{v}{(1-IoU)+v}$$
$$v=\frac{4}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2$$

最终使用这些损失函数在不同的模型进行了比较，详情可以参考论文。

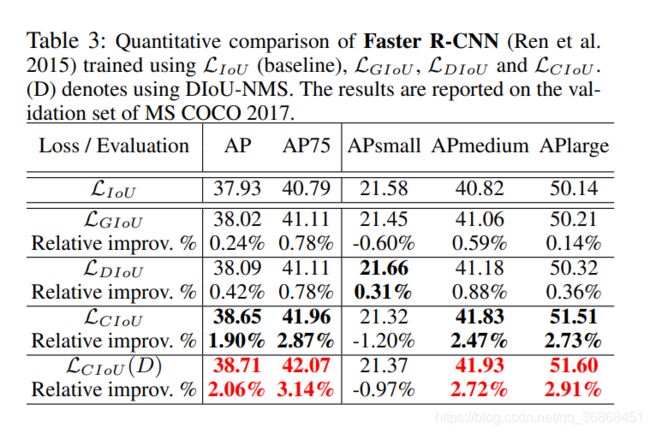
3.1. 代码实现

仿照上面的方法，实现CIoU的代码如下（需要注意bbox的表示类型，应该是[x1,y1,x2,y2],而不是[x,y,w,h]）：

def getWidthAndHeight(bbox):
    return bbox[2]-bbox[0],bbox[3]-bbox[1]

def getCIoU(bbox_gt,bbox_pd):
    #1. get bbox_hat
    bbox_cvx = getConvexShape(bbox_gt,bbox_pd)
    #2. caculate the area of ground truth
    area_bbox_gt = getBboxArea(bbox_gt)
    #3. caculate the area of predictions
    area_bbox_pd = getBboxArea(bbox_pd)
    #4. caculate the area of Intersection
    bbox_inter = getIntersection(bbox_gt,bbox_pd)
    area_bbox_inter = getBboxArea(bbox_inter)
    
    #5. caculate the center points
    center_point_gt = getCenterPoint(bbox_gt)
    center_point_pd = getCenterPoint(bbox_pd)

    #6. caculate the distance between the center point gt and the center point pd
    rho_2 = getDistance(center_point_gt, center_point_pd) ** 2

    #7. caculate the diag distance of cvx shape
    c_2 = getDistance(bbox_cvx[0:2], bbox_cvx[2:4]) ** 2

    #8. caculate IoU
    IoU = area_bbox_inter / ( area_bbox_gt + area_bbox_pd - area_bbox_inter )

    #9. caculate the width and height of the bboxes
    w_gt,h_gt = getWidthAndHeight(bbox_gt)
    w_pd,h_pd = getWidthAndHeight(bbox_pd)

    #10. caculate the aspect ratio in cIoU
    ciou_v = 4/(math.pi ** 2) * (math.atan(w_gt/h_gt) - math.atan(w_pd/h_pd)) ** 2

    #11. caculate the alpha in cIoU
    ciou_alpha = ciou_v / (1 - IoU + ciou_v)

    #12. caculate the ciou
    CIoU = IoU - rho_2 / c_2  - ciou_alpha * ciou_v

    return IoU,CIoU

4. 后记

4.1. 不理解的问题

CIoU为什么惩罚项要写成那个样子原作者并没有解释

4.2. 自己的想法

CIoU原作者提出的三点因素虽说都有影响，但是并没有针对这些因素进行定量的研究，比如这些因素中究竟哪一个的影响最大？