扩展卡尔曼滤波EKF用于多源传感器融合

1.Kalman Filters

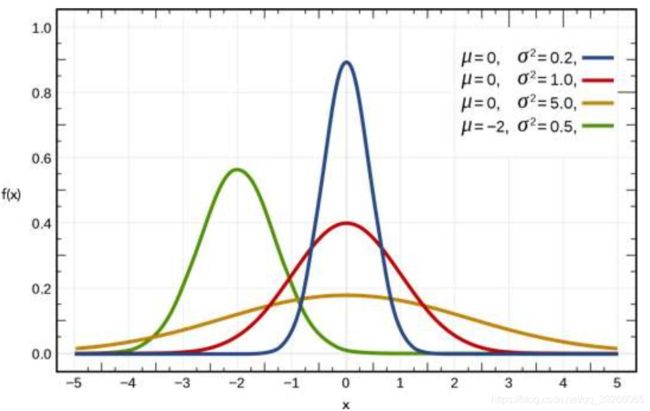
在跟踪一辆运行的车时，当$\sigma$越小，表明确定因素越多。

测量值更新使用贝叶斯规则，而预测是全概率公式，也是一种加权平均，他们之间通过高斯实现。
假设我们已知先验告诉我们有辆车的位置分布如下黑色线所示，一个较宽的高斯分布，其均值为$\mu$。而测量值信息告诉的车辆位置如蓝色线所示，其均值为$v$，测量值拥有更小的协方差。相比较，该例子中测量值所给出的位置信息更多。

因此，利用先验和测量值信息，所得到的新的高斯分布如下，均指在两者之间，但相比较组成他的两个高斯分布来说更加确定！他的协方差更小！因为它获得了更多的信息。

Motion update即预测值，也就是简单的相加。因为在运动过程中丢失了确定信息，所以其不确定性更大，$\sigma$越大。

了解了一维中的卡尔曼滤波后，接下来扩展到二维：

可以通过$t=0,1,2$时刻得到车辆的速度，因此可以做出一个当$t=3$时很好的预测，此时的传感器并没有真正的得到速度信息，其只有位置信息，而速度是通过位置推断得到。
在卡尔曼滤波中，即使传感器没有直接的速度信息，也可以得到目标的速度，然后去预测将来的位置信息！

创建一个二维的估计，一个是位置还有一个则是速度，速度可以为负值。如果初始知道位置，但是并不知道速度，此时用一个高斯分布在正确的位置附近去表示速度，接下来去预测位置，假设速度为1，则$x=2$。因此如下红色部分则为预测的位置信息！

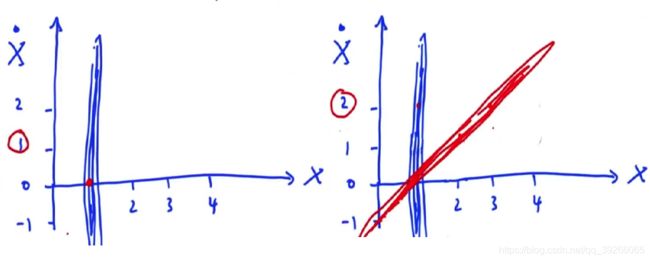
可以得到位置信息与速度之间的关系，而观测信息并不能告诉我们速度，而是关于位置的信息：

通过该测量信息可以估计速度，和当前的位置，此时便可以估计下一时刻的位置信息。
综上可以得到卡尔曼滤波：
$$p_k=p_{k-1}+\Delta t{v}_{k-1}$$ $$v_k=v_{k-1}$$矩阵形式：
$$\begin{gathered} {\hat{\mathbf{x}}}_k=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]{\hat{\mathbf{x}}}_{k-1} \\ ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1} \end{gathered}$$

参考资料：1.卡尔曼滤波简介 2.Sensor Fusion 课程

2. Lidar and Radar Fusion with Kalman Filters in C++

Lesson Map and Fusion Flow

扩展的卡尔曼滤波能够处理更加复杂的运动模型和测量模型，上图为一个整体的流程。有两个传感器：LIDAR和RADAR，由传感器提供信息用于估算状态，这个状态包含了2D位置和速度。

每次收到传感器的测量数据，估算函数将会被触发，分为两部分，状态预测(PREDICT)和测量值更新(Update)。在预测过程中，预测到行人的状态和协方差。测量值更新方式取决于传感器类型，这里有两种传感器，如果当前测量由LASER产生，仅仅使用标准的卡尔曼滤波去更新行人的状态。然而RADAR测量值涉及到非线性函数，因此需要使用其他的方法去处理，例如扩展的卡尔曼滤波。

Refresh Estimation Problem

卡尔曼滤波就是由简单无限循环预测和更新的步骤组成，然而当存在两个传感器的时候，每个传感器都有它自己的预测和更新的计划。换句话说，对于行人的位置和速度更新是异步的。

接下来通过一个例子去看看它是如何工作的。行人在时间$k$的状态分布的均指为$X$，协方差为$P$，在$k+1$时刻，我们仅仅接收到了$laser$的测量数据，在测量值更新前第一件事需要去做一个预测，关于行人从$k$时刻到$k+1$时刻的位置，第二件事是测量值更新，在这里我们结合行人的预测状态和新的$laser$测量值，现在我们更加相信行人在$t+1$时刻的位置。

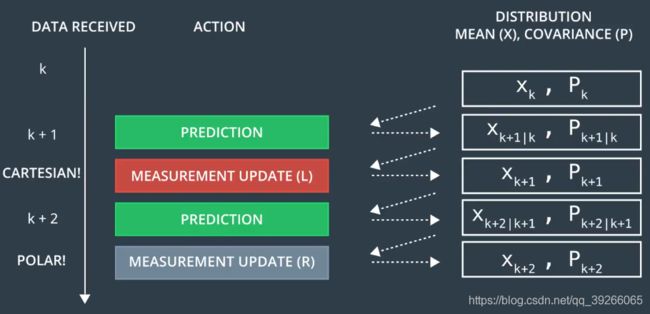
现在当收到$radar$在$t+2$时刻的测量值，首先我们再一次预测行人从$k+1$到$k+2$时刻的状态，此时$radar$是和$laser$完全一样的作用，所改变的是测量值更新步骤。$laser$提供的测量值是在笛卡尔坐标系下，而$radar$提供的测量值在极坐标系下，因此我们需要使用不同的测量值更新方法。

Kalman Filter Intuition

我们的任务是跟踪一个行人的状态$X$，由位置$p$和速度$v$组成。
$$x=\left(\begin{array}{c}p\\ v\end{array}\right)$$
当设计一个卡尔曼滤波，需要去定义两个线性方程。
状态转换函数：表示状态从$k-1$到$k$时刻是如何变化的。
$$x^{\prime }=f(x)+v=Fx+Bu+v=Fx+v,v\backsim N(0,Q)$$
测量函数：表示测量值是如何计算的，以及他和预测状态$X$之间的关系。
$$z=h(x^{\prime })+w=Hx+w$$
其中$f(x),Fx,h(x^{\prime })$属于我们模型中确定的部分，而$v,w$则代表随机部分，换句话说，随机噪声影响了预测和测量值更新步骤。因此通过使用一个匀速线性运动模型 $p^{\prime }=p+v\Delta t$，行人上一时刻的位置加上速度乘上时间。因为速度是匀速的，所以新的速度和上一时刻相同$v^{\prime }=v$。因此可以通过矩阵去描述：
$$\left(\begin{array}{c}{p}^{\prime }\\ v^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right)\left(\begin{array}{c}p\\ v\end{array}\right)$$
对于测量函数，我们的车辆仅仅感受到行人的位置$z=p^{\prime }$，因此它可以由如下矩阵表示：
$$z=\left(\begin{array}{cc}1& 0\end{array}\right)\left(\begin{array}{c}{p}^{\prime }\\ v^{\prime }\end{array}\right)$$

正如我们所知道的，卡尔曼滤波算法由预测（预测我们的状态和协方差）和测量更新（矫正），在矫正部分使用最新的测量值去更新估计的状态和它的不确定性。

State Prediction

以上则完成了一维的卡尔曼滤波，接下来扩展到二维：

如上图所示，变成一个四维的状态向量：$$x=\left(\begin{array}{c}{p}_x\\ p_y\\ v_x\\ v_y\end{array}\right)$$同理，使用一个相同的匀速线性运动模型：$$\{\begin{array}{l}{p}_x^{\prime }=p_x+v_x\Delta t+v_{px}\\ p_y^{\prime }=p_y+v_y\Delta t+v_{py}\\ v_x^{\prime }=v_x+v_{vx}\\ v_y^{\prime }=v_y+v_{vy}\end{array}$$因此可以得到如下的状态转换方程：$$\left(\begin{array}{c}{p}_x^{\prime }\\ p_y^{\prime }\\ v_x^{\prime }\\ v_y^{\prime }\end{array}\right)=\left(\begin{array}{cccc}1& 0& \Delta t& 0\\ 0& 1& 0& \Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{p}_x\\ p_y\\ v_x\\ v_y\end{array}\right)+\left(\begin{array}{c}{v}_{px}\\ v_{py}\\ v_{vx}\\ v_{vy}\end{array}\right)$$

除此之外，观测时间间隔也不再是常数，而是不断变化的！

上面的等式可以简化为$x^{\prime }=Fx+noise$

• 运动噪声和过程噪声指的是相同的情况：预测位置时对象位置的不确定性。 该模型假定速度在两个时间间隔之间是恒定的，但实际上我们知道物体的速度会由于加速度而发生变化。 该模型通过过程噪声包括了这种不确定性。
  两次时间间隔越大不确定性也就越大，随机噪声会随着预测时间之间的间隙增加而增加。
• 测量噪声是指传感器测量中的不确定性。

Process Covariance Matrix

首先如何用运动学方程去表达加速度，然后使用该信息去推导协方差矩阵$Q，\mu \backsim N(0,Q)$。我们拥有同一个行人初始和最终的速度，从运动学方程中可以根据上一时刻的状态变量推导出当前的位置和速度，包括速度的变化（加速度）。
$$a=\frac{\Delta v}{\Delta t}=\frac{v_{k+1}-v_k}{\Delta t}$$
因为速度并不是匀速的，并且加速度是不知道的，因此可以将它添加到噪声$\mu$的部分。
$$\{\begin{array}{l}{p}_x^{\prime }=p_x+v_x\Delta t+{\mu }_{px}\\ p_y^{\prime }=p_y+v_y\Delta t+{\mu }_{py}\\ v_x^{\prime }=v_x+{\mu }_{vx}\\ v_y^{\prime }=v_y+{\mu }_{vy}\end{array}⟹\{\begin{array}{l}{p}_x^{\prime }=p_x+v_x\Delta t+\frac{a_x\Delta t^2}{2}\\ p_y^{\prime }=p_y+v_y\Delta t+\frac{a_y\Delta t^2}{2}\\ v_x^{\prime }=v_x+a_x\Delta t\\ v_y^{\prime }=v_y+a_y\Delta t\end{array}$$
噪声$\mu$可以分为两部分：
$$\mu =\{\begin{array}{l}\frac{a_x\Delta t^2}{2}\\ \frac{a_y\Delta t^2}{2}\\ a_x\Delta t\\ a_y\Delta t\end{array}=\left(\begin{array}{cc}\frac{\Delta t^2}{2}& 0\\ 0& \frac{\Delta t^2}{2}\\ \Delta t& 0\\ 0& \Delta t\end{array}\right)\left(\begin{array}{c}{a}_x\\ a_y\end{array}\right)=Ga$$$G$是一个$4\ast 2$的不包括随机变量的矩阵，而$a$是一个$2\ast 1$的包含随机加速度的部分。在我们噪声向量的基础上，可以定义一个新的协方差矩阵Q，该协方差矩阵由噪声向量的期望值定义。
$$Q=E[\mu {\mu }^T]=E[Ga{a}^T{G}^T]$$$$Q=GE[a{a}^T]G^T=G\left(\begin{array}{cc}{\sigma }_{ax}^2& {\sigma }_{axy}\\ {\sigma }_{axy}& {\sigma }_{ay}^2\end{array}\right)G^T=G{Q}_v{G}^T$$因为G是不含有随机变量的，因此可以将其移到期望值计算的外边，我们假设$ax$和$ay$是互不相关的噪声，因此${\sigma }_{axy}=0$，最终所得到的协方差矩阵Q为：
$$Q=G{Q}_v{G}^T=\left(\begin{array}{cccc}\frac{\Delta t^4}{4}{\sigma }_{ax}^2& 0& \frac{\Delta t^3}{2}{\sigma }_{ax}& 0\\ 0& \frac{\Delta t^4}{4}{\sigma }_{ay}& 0& \frac{\Delta t^3}{2}{\sigma }_{ay}^2\\ \frac{\Delta t^3}{2}{\sigma }_{ax}^2& 0& \Delta t^2{\sigma }_{ax}^2& 0\\ 0& \frac{\Delta t^3}{2}{\sigma }_{ay}^2& 0& \Delta t^2{\sigma }_{a_y}^2\end{array}\right)$$

Laser Measurements

以上，我们已经定义了运动模型，接下来定义2D激光传感器的测量模型，测量值向量$z$，测量矩阵$H$，协方差矩阵$R$。虽然激光雷达给出的点云数据，但可以通过目标检测得到目标的位置$(p_x,p_y)$。
$$z=\left(\begin{array}{c}{p}_x\\ p_y\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right)\left(\begin{array}{c}{p}_x^{\prime }\\ p_y^{\prime }\\ v_x^{\prime }\\ v_y^{\prime }\end{array}\right)$$对于激光传感器，我们有一个2D测量向量。 每个位置分量$(p_x,p_y)$都受到随机噪声的影响，因此我们的噪声向量$w$由着和$z$一样的维度，因此得到测量值噪声的协方差矩阵$R$为：
$$R=E[w{w}^t]=\left(\begin{array}{cc}{\sigma }_{px}^2& 0\\ 0& {\sigma }_{py}^2\end{array}\right)$$矩阵R代表我们从激光传感器接收到的位置测量结果中的不确定性。通常，随机噪声测量矩阵的参数将由传感器制造商提供。

Radar Measurements

接下来我们将结合$radar$测量值到卡尔曼滤波中，即使$laser$已经提供了高精度的行人位置，但是仍然没有一个办法可以直接观察到他的速度，这便是$radar$可以使用多普勒效应做的事情。$radar$可以直接测量移动物体的径向速度，但是相比$laser$传感器，$radar$有较低的空间分辨率。

在$radar$中，状态量和运动方程同$laser$中一样，但是其坐标系不同，$x$轴代表车辆的运动方向，$y$轴则是运动方向的左侧。
RANGE：$\rho$代表从雷达原点到行人之间的距离；
BEARING：$\phi$代表这条射线与$x$轴即运动方向的角度；
RADIAL VELOCITY：$\dot{\rho }$代表在该条射线方向下的速度。
因为其三者是互不相关的，因此其测量值的协方差矩阵为$3\ast 3$的对角矩阵。

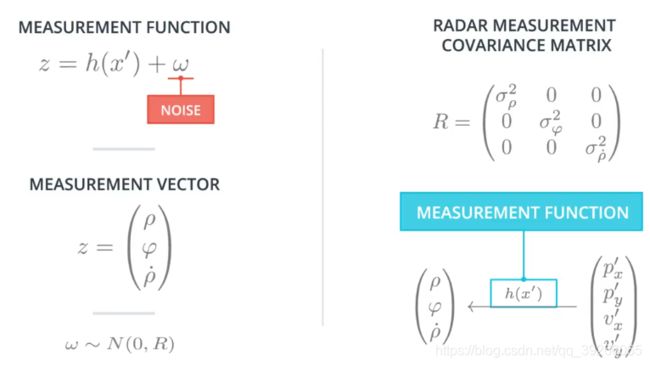
来自激光雷达$H$矩阵和来自雷达的$h(x)$方程实际上是在完成相同的工作； 在更新步骤中它们都需要解决$y=z-H{x}^{\prime }$。但是对于雷达来说，没有将状态向量$x$映射到极坐标的$H$矩阵，因此需要手动计算映射以将笛卡尔坐标转换为极坐标。
这是$h$函数，它指定如何将预测的位置和速度映射到$\rho ,\phi ,\dot{\rho }$的极坐标。

此处$h$为一个非线性函数，不再适合卡尔曼滤波！

Extended Kalman Filter

如果我们将此高斯映射到非线性函数，其结果不再是一个高斯分布。因此需要线性化$h(x)$函数，这种关键的思想被叫做扩展卡尔曼滤波。
因此我们必须近似测量值函数$h$通过一个线性函数，该线性函数是原始高斯均值位置的切线！此时所得到结果便符合高斯分布。

因此如何线性化一个非线性函数？扩展的卡尔曼滤波使用的方法叫做一阶泰勒展开式。
$$h(x)\approx h(\mu )+\frac{\partial h(\mu )}{\partial x}(x-\mu )$$
线性化$h(x)$函数的雅可比矩阵如下：

EKF Algortihm Generalization

我们将$u$设为0。高斯分布的不确定性出现在$Q$矩阵中。对于一个非线性函数，需要计算其雅可比矩阵$F_j,H_j$将其线性化。
对于扩展的卡尔曼滤波，首先是线性化非线性的预测和测量值函数，然后使用同样的原理去估计状态值。