k近邻算法原理以及代码

前言

K近邻(k-nearest neighbor, K-NN)，从名字可以看出是找到k个最近的邻居。它是一种基本的分类与回归方法，属于判别模型。虽然在《统计学习方法》中只讨论他的分类问题，但是其实回归问题也与分类问题类似。k近邻算法在我看来就是一个近朱者赤，近墨者黑的算法。

一. 模型

KNN没有显式的学习过程，它不像感知机需要学习得到一个超平面划分区间，收到新样本后按照划分的区域分类。KNN不对已知数据点做处理学习，待收到新样本后根据数据点直接进行处理(数k个近邻分类)。
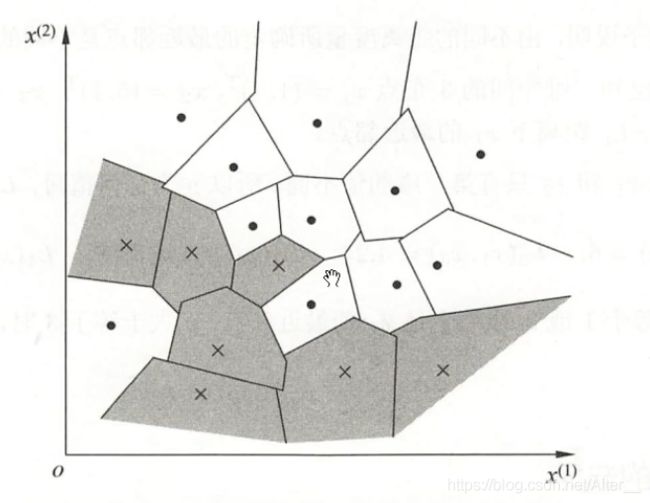
利用训练数据对特征空间的划分得到的特征空间是最终的KNN模型。完成后特征空间如下，每一个点或者叉对应一个区域，如果新的点落近一个区域表示新点距离该区域中心点或者叉是最近的。

二.策略

KNN的模型由三个基本要素决定

1. 距离度量：两个实例点的距离可以反应实例点的相似程度。距离度量有多种如欧式距离、曼哈顿距离等。
   
   
2. k值的选择
   k值选择使用交叉验证法：首先k=1，然后测试已知数据集看得到的准确率；再k=2，k=3…；选择准确率最高的k。
3. 分类决策规则
   多数表决规则：使误分类率最小的，多数类决定输入实例类(同流合污)。

三.算法

四.kd树

从算法不难理解，k近邻就是在已知的数据中找最近的k数据，找的过程肯定需要比较距离大小，当数据小的时候我们一个一个比较没有问题，但是数据变多了怎么办？为了能快速检索，排除肯定距离会变大的点，我们可以使用kd树来提高效率。

• 算法：构造kd树

1. 先以x的1维(x_(1))做坐标轴，先把这个坐标轴切分。把给定的数据集按照1维的数从小到大排序，找到中位数(偶数的话，随便选择靠左还是靠右)。这个中位数成为根节点，以此为中心，坐标轴被划分左边区域和右边区域。
2. 我们如果要找深度为j的节点(比如找完根节点要找深度为1的节点啦)，首先计算现在的我们要以哪个维度的x_(l)做坐标轴，计算公式为l=j(mod k)+1。找到需要划分的维度之后，再执行第一步骤。
3. 确定一个维度，确定这个维度下的中位数
   ->中位数做垂直于维度的垂线划分左右区域
   ->左右区域再开始找各自的维度、中位数划分区域
   ->直到所有的实例都被当做中位数切割完特征空间结束。

• 算法：搜索kd树最近邻点

1. 从根节点出发，递归的向下访问kd树。每到一层都要记得把目标点的维度与当初构造kd树使用的维度相比较，小的向左，大的向右，直到叶子节点。例如，当初建树时，在深度1的时候用了第二维度进行排序比较的，那么现在使用目标点的第二维度与节点们比较。
2. 此时叶子节点当作当前最近的点，该点到目标点的距离就是半径，有小于半径的就可以替换当前最近点。那么我们需要向上回退看还有没有更近的点。
3. 回退到当前节点的父亲节点作为当前节点，如果当前节点离目标节点更近那么就替换当前最近点。
4. 必须检查父亲节点的另一个子节点，看看它的区域有没有更近的点。具体要看另一子结点的区域是否会与当前最近点与目标点所形成的圆是否有交集。相交则可能存在，那么我们把当前节点移动到另一个子节点上进行kd搜索；不相交绝对不存在，重新到第3步，之后就是第3、4步的交替，直到回退到根节点结束。

五.代码

# 最原始得代码，未涉及构建和使用搜索树
# k近邻,线性扫描,二维空间
import random
import numpy as np
import matplotlib.pyplot as plt
import math

from matplotlib.patches import Circle


def createDataSet():
    random_points = set([(random.randint(1, 100), np.random.randint(1, 100)) for _ in range(100)])  # 随机生成100个点
    points = np.array(list(random_points))
    label = np.zeros(points.shape[0])
    for i in range(points.shape[0]):
        label[i] = random.choice([-1, 1])
    return points, label


def plant(data, label, z, r, point):
    fig = plt.figure()  # 画布
    ax = fig.add_subplot(1, 1, 1)
    for i in range(data.shape[0]):
        if label[i] == 1:
            plt.plot(data[i][0], data[i][1], 'ro')  # 红点
        else:
            plt.plot(data[i][0], data[i][1], 'bo')  # 蓝点
    plt.plot(point[0], point[1], z)
    circle = plt.Circle((point[0], point[1]), r, alpha=0.1, color=z[0])
    ax.add_patch(circle)
    plt.show()


def cal_distance(x, y):
    return math.sqrt((x[0]-y[0])**2+(x[1]-y[1])**2)


def knnclassifier(train_set, train_label, point, k):
    arr = [150]*k
    lab = [1]*k
    z = 0   # 结果
    index = 0
    for i in train_set:
        distance = cal_distance(i, point)
        if distance < max(arr):
            j = arr.index(max(arr))     # 获得替换位置得下标
            arr[j] = distance
            lab[j] = train_label[index]
            print(arr, i, index, lab)
        index += 1
    for i in lab:
        if i == 1:
            z += 1
        else:
            z -= 1
    if z > 0:
        return 'rv', max(arr)
    else:
        return 'bv', max(arr)


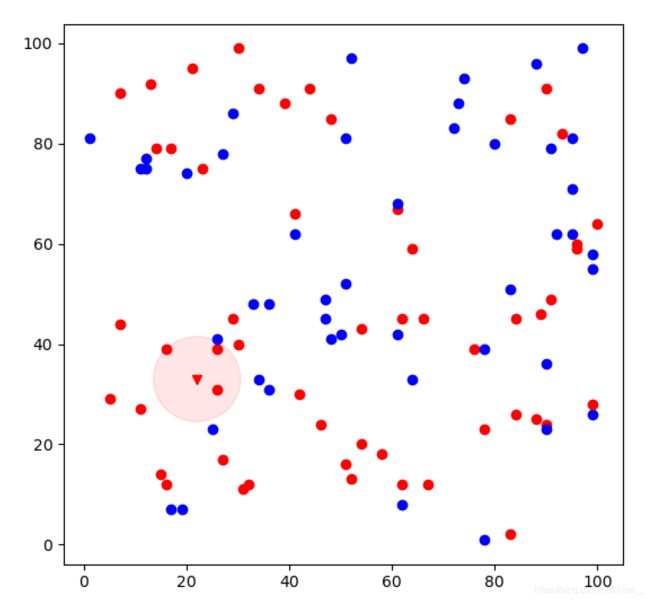
if __name__ == "__main__":
    data, label = createDataSet()
    # print(data, label)
    point = [22, 33]
    z,r = knnclassifier(data, label, point, k=3)
    plant(data, label, z, r, point)

# kd搜索最近k个数据
import numpy as np
import heapq   # 堆


class Node:
    def __init__(self, point, demo=0, left=None, right=None):
        self.point = point
        self.demo = demo    # 所在维度
        self.right = right
        self.left = left
        self.dist = -np.inf  # 欧式距离, heapdreplace只能替换最小值，不能替换最大值，所以取负号让它以为替换了最小值

    def __lt__(self, other):    # 富比较，节点与节点之间不能直接比较
        return self.dist < other.dist


class KDTree:
    def __init__(self, data):
        self.demos = data.shape[1]   # 一共多少维
        self.root = self.createTree(data, 0)
        self.heap = []      # 用列表转化堆，存放最近的k个点

    def createTree(self, dataset, sp):
        if len(dataset) == 0:   # 终止递归
            return None
        dataset_sorted = dataset[np.argsort(dataset[:, sp])]
        # np.argsort()返回后序数组，值从小到大排序后的原下标号
        # dataset[:, :] 二维数组得切片, 逗号前面是行后面是列
        # dataset[索引] 索引可以是数组
        # print(dataset_sorted)
        mid = len(dataset_sorted) // 2       # 中位数索引
        left = self.createTree(dataset_sorted[:mid], (sp+1) % self.demos)
        right = self.createTree(dataset_sorted[mid+1:], (sp+1) % self.demos)
        parentNode = Node(dataset_sorted[mid], sp, left, right)
        # 先分到最小得叶子节点，再组装树
        return parentNode

    def nearest(self, x, k):
        def visit(node):    # node表示当前点
            if node != None:
                # 递归调用到叶子节点
                dis = node.point[node.demo]-x[node.demo]
                visit(node.left if dis > 0 else node.right)
                # 计算目标点到当前点的欧式距离
                curr_dis = np.linalg.norm(x-node.point, 2)   # 二范数x是x-node，变成欧式距离
                node.dist = -curr_dis       # 取负号存储，最大的排在最前面

                if len(self.heap) < k:
                    heapq.heappush(self.heap, node)     # 放入堆函数
                else:
                    if heapq.nsmallest(1, self.heap)[0].dist < -curr_dis:    # nsmallest(个数，集合)返回最小的多个值。但是在这里我们找到的是最大的
                        heapq.heapreplace(self.heap, node)      # 弹出的是最小值其实是距离最远的
                if abs(heapq.nsmallest(1, self.heap)[0].dist) > abs(dis) or len(self.heap) < k:   # 以当前k中最远的点画圆, 加后面是因为这个是搜索最近的k个，只看一边的点，点可能不够
                    visit(node.left if dis < 0 else node.right)     # 在当前节点是叶子节点的时候这个没有用
        node = self.root
        visit(node)
        for i in range(k):
            print(self.heap[i].point)


if __name__ == '__main__':
    # 传数据
    train_point = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
    kd = KDTree(train_point)
    kd.nearest(np.array([6, 5]), 3)

https://www.cnblogs.com/ssyfj/p/13053055.html
kd搜索最近k个数据的代码可以说完全参考了，贴上去主要是一些注释和理解，知道他为什么这么做。