完整代码
JavaScript 实现
https://github.com/Jiacheng78...
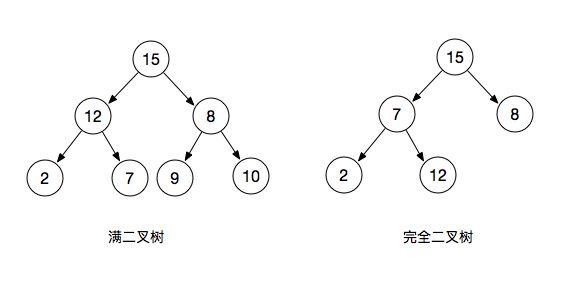
堆的概念
一般堆排序里的堆指的是二叉堆,是一种完全二叉树。完全二叉树有一个性质是,除了最底层,每一层都是满的,这使得堆可以利用数组来表示,每个结点对应数组中的一个元素。
二叉堆有两种:最大堆和最小堆。最大堆所有父节点的值大于子节点的值,最小堆所有父节点的值小于子节点的值。
显然,最大堆堆顶元素必然是堆中最大的元素,最小堆堆顶元素是堆中最小的元素
堆排序实现
下面使用 JavaScript 代码介绍堆排序实现。
首先需要初始化一个二叉堆,前面介绍了二叉堆实际上就是一个数组,因此初始化非常简单:
constructor(arr) {
this.data = [...arr];
this.size = this.data.length;
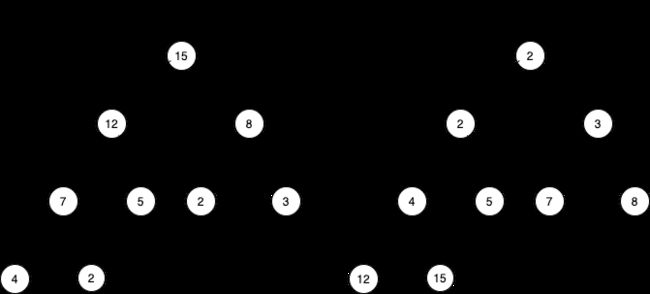
}在初始化的时候,如果某一结点不符合二叉堆的性质,需要将该节点与两个子节点进行交换。具体流程是,当前节点与两个子节点进行对比,如果不符合二叉堆性质,取三个里面的最大值并进行交换,交换后的子节点继续递归进行后续子树的交换:
maxHeapify(i) {
let max = i; // 保存最大的节点下标
if (i >= this.size) return;
const left = i * 2 + 1; // 左节点下标
const right = i * 2 + 2; // 右节点下标
if ((left < this.size) && (this.data[left] > this.data[max])) {
max = left;
}
if ((right < this.size) && (this.data[right] > this.data[max])) {
max = right;
}
if (max === i) return; // 如果最大节点是其本身,不进行交换
[this.data[i], this.data[max]] = [this.data[max], this.data[i]];
return this.maxHeapify(max);
}关键代码:
const left = i * 2 + 1; // 获取左节点
const right = i * 2 + 2; // 获取右节点
上面的maxHeapify函数只能对某一结点进行对调,无法对整个数组进行重构。构造一个最大堆需要获取到所有的分支节点(不含叶子节点),然后对每个分支节点依次进行递归重构:
rebuildHeap() {
// 获取分支节点
const L = Math.floor(this.size / 2);
for(let i = L - 1; i >= 0; i--){
// 每个i都代表一个分支节点的下标
this.maxHeapify(i);
}
}关键代码:
const L = Math.floor(this.size / 2); // 获取分支节点
注意上一步完成后数组还并没有完成排序,只是基本有序,下面进行排序操作。从最后一个元素开始,和堆顶元素交换,然后size-1将最后一个元素分离出堆,调用maxHeapify维持最大堆性质。由于堆顶元素必然是堆中最大的元素,所以一次操作之后,堆中存在的最大元素被分离出堆,重复n-1次之后,数组排列完毕:
sort() {
for(let i = this.size - 1; i > 0; i--){
[this.data[0], this.data[i]] = [this.data[i], this.data[0]];
this.size--; // 将交换后的元素分离出堆
this.maxHeapify(0);
}
this.size = this.data.length; // 排序完成后重新获取size
}如果是从小到大排序,用最大堆;从大到小排序,用最小堆
时间复杂度与稳定性
n个元素的完全二叉树的深度h=floor(logn)
堆调整时间复杂度:O(log n)
建堆的时间复杂度:O(n)
堆排序的时间等于建堆和进行堆调整的时间之和:O(nlog n + n) = O(nlog n)
堆排序是不稳定的算法,它不满足稳定算法的定义。它在交换数据的时候,是比较父结点和子节点之间的数据,所以,即便是存在两个数值相等的兄弟节点,它们的相对顺序在排序也可能发生变化。
面试题
美团面试题:
一个没有排序的数组,不对整个数组进行排序,如何找出最大的 m 个元素
(不用写代码,讲出思路即可)
使用最大堆的堆排序。经过上面的分析可以看出,堆排序有个特点,每一次循环后堆顶元素被分离出堆,由于最大堆堆顶元素始终都是这个堆中最大的元素,因此只需要循环 m 次就能找出数组中最大的 m 个元素,无需对整个数组进行排序。
字节面试题:
Leetcode 215. 数组中的第K个最大元素
给你1亿个数字,找出最大的前K个
这道题有多种解法,最简单的就是先快速排序,然后获取下标 len - k 的元素,时间复杂度 O(nlog n)。也可以利用与快排类似的 partition 思想。
如果数组长度不是特别大,排序是没问题的。但是如果数组特别大(例如题目中给的1亿个),别说排序了,可能内存里都放不下了,这种情况就需要用到下面的 优先队列思想。
还有一种就是利用优先队列思想。优先队列可以看作一种不完全的堆排序,正常的堆排序会循环 n - 1 次,每次都 pop() 出一个堆顶元素,最终将整个数组进行排序,优先队列可以循环指定次数,pop() 出前 k 个最大或最小的元素,这样就不用对整个数组进行排序。优先队列有两种思路:
思路1:把len个元素都放入一个最小堆中,然后再pop()出len - k个元素,此时最小堆只剩下k个元素,堆顶元素就是数组中的第k个最大元素
思路2:把len个元素都放入一个最大堆中,然后再pop()出k - 1个元素,因为前k - 1大的元素都被弹出了,此时最大堆的堆顶元素就是数组中的第k个最大元素
实现一个 pop 函数,一次从堆顶弹出一个元素:
pop() {
let lastNode = this.size - 1; // 获取堆中最后一个元素的下标
[this.data[0], this.data[lastNode]] = [this.data[lastNode], this.data[0]];
this.size--; // 堆顶元素与最后一个元素交换,将交换后的元素分离出堆
this.maxHeapify(0);
}
peek() {
// 获取当前堆顶元素
return this.data[0];
}之前的 sort 方法相当于进行 n - 1 次 pop 操作,这边只需要进行 k - 1 即可:
const heap = new Heap([15, 2, 8, 12, 5, 2, 3, 4, 7]);
heap.rebuildHeap();
// heap.sort();
for (let i=0; iJava 使用内置的优先队列(PriorityQueue)实现:
import java.util.PriorityQueue;
public class Solution {
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
// 使用一个含有 len 个元素的最小堆,默认是最小堆,可以不写 lambda 表达式:(a, b) -> a - b
// 如果是最大堆应写成:(a, b) -> b - a
PriorityQueue minHeap = new PriorityQueue<>(len, (a, b) -> a - b);
for (int i = 0; i < len; i++) {
minHeap.add(nums[i]); // 添加元素
}
for (int i = 0; i < len - k; i++) {
minHeap.poll(); // 弹出堆顶元素
}
return minHeap.peek(); // 获取堆顶元素
}
}