1 什么是”最小二乘法”呢？

线性回归是很常见的一种回归，线性回归可以用来预测或者分类，主要解决线性问题。

一元线性回归、多元线性回归、逻辑斯谛回归、广义线性回归、非线性回归的关系　

插图摘自周志华《机器学习》及互联网

线性回归过程主要解决的就是如何通过样本来获取最佳的拟合线。现在使用得比较广泛的就是梯度下降和最小二乘法
，它是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。
在有监督学习问题中，线性回归是一种最简单的建模手段。给定一个数据点集合作为训练集，线性回归的目标是找到一个与这些数据最为吻合的线性函数。对于2D数据，这样的函数对应一条直线。

线性模型在二维空间中就是一条直线，在三维空间是一个平面，高维空间的线性模型不好去描述长什么样子；如果这个数据集能够用一个线性模型来拟合它的数据关系，不管是多少维的数据，我们构建线性模型的方法都是通用的。

学习 TensorFlow 让我的思维发生了变化。
计算机本质上是一种数学的工具，而我在学习编程的时候，思维也不可避免地收到了影响。传统的编程思想，常常认为程序就应该像数学定理或者数学函数一样，给出一个确定的结果。这是一种基于逻辑推导的思维习惯。
然而，做实验的科学家们的思维却不像数学家一样。实验科学家通过做实验收集数据，再根据数据推测其中蕴含的某种规律。

定义：最小二乘法（又称最小平方法）是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。
作用：利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
原则：以”残差平方和最小”确定直线位置(在数理统计中，残差是指实际观察值与估计值之间的差)

基本思路：对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn），对于平面中的这n个点，可以使用无数条曲线来拟合。而线性回归就是要求样本回归函数尽可能好地拟合这组值，也就是说，这条直线应该尽可能的处于样本数据的中心位置。因此，选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。

2 如何理解最小二乘法

用一个具体的例子来说明，可能会让读者更加容易理解：
小明是跑运输的，跑1公里需要6块，跑2公里需要5块（那段时间刚好油价跌了），跑3公里需要7块，跑4公里需要10块，请问跑5公里需要多少块？
如果我们有初中数学基础，应该会自然而然地想到用线性方程组来做，对吧。
y=β1+xβ2
这里假定x是公里数，y是运输成本（β1和β2是要求的系数）。我们把上面的一组数据代入得到这么几个方程：

β1+1β2=6
β1+2β2=5
β1+3β2=7
β1+4β2=10

如果存在这样的β1和β2，让所有的数据（x，y）=（1,6），（2,5），（3,7），（4，10）都能满足的话，那么解答就很简单了，β1+5β2就是5公里的成本，对吧。
但遗憾的是，这样的β1和β2是不存在的，上面的方程组很容易，你可以把前面两个解出来得到一组β1和β2，后面两个也解出来同样得到一组β1和β2。这两组β1和β2是不一样的。

形象地说，就是你找不到一条直线，穿过所有的点，因为他们不在一条直线上。
可是现实生活中，我们就希望能找到一条直线，虽然不能满足所有条件，但能近似地表示这个趋势，或者说，能近似地知道5公里的运输成本，这也是有意义的。

其实最小二乘法也是这样，要尽全力让这条直线最接近这些点，那么问题来了，怎么才叫做最接近呢？直觉告诉我们，这条直线在所有数据点中间穿过，让这些点到这条直线的误差之和越小越好。这里我们用方差来算更客观。也就是说，把每个点到直线的误差平方加起来：

##最小二乘法
import numpy as np   ##科学计算库
import scipy as sp   ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt  ##绘图库
from scipy.optimize import leastsq  ##引入最小二乘法算法

'''
     设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([1,2,3,4])
Yi=np.array([6,5,7,10])

'''
    设定拟合函数和偏差函数
    函数的形状确定过程：
    1.先画样本图像
    2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''

##需要拟合的函数func :指定函数的形状
def func(p,x):
    k,b=p
    return k*x+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

'''
    主要部分：附带部分说明
    1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
    2.官网的原话（第二个值）：Value of the cost function at the solution
    3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)
    4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost："+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))

'''
   绘图，看拟合效果.
   matplotlib默认不支持中文，label设置中文的话需要另行设置
   如果报错，改成英文就可以
'''

#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="sample data",linewidth=2)

#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="Fitting straight line",linewidth=2)
plt.legend(loc='lower right') #绘制图例
plt.show()

k= 1.400000000000871 b= 3.499999999964018
cost：1
求解的拟合直线为:
y=1.4x+3.5

求解的拟合直线为:
y=1.4x+3.5

这个函数也就是我们要的直线，这条直线虽然不能把那些点串起来，但它能最大程度上接近这些点。也就是说5公里的时候，成本为3.5+1.4x5=10.5块，虽然不完美，但是很接近实际情况。

3 实际应用的一个完整示例

整个过程分七步，每步都放上了完整的代码。

实验数据：

身高/cm：
105,109,119,120,120,120,121,121,121,123,
123,123,123,124,125,125,125,126,126,126,
126,126,127,127,127,127,127,129,130,130,
130,131,131,131,132,132,132,132,132,133,
134,134,134,136,136,137,137,142

体重/kg：
24,28,25,31,22,21,21,22,20,23,
22,23,22,21,28,23,22,21,26,24,
21,27,25,25,24,24,21,24,25,23,
28,29,26,26,31,27,27,31,25,34,
23,26,32,36,26,40,28,44

3.1 第一步：准备样本数据并绘制散点图

1）代码及其说明

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重

#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="sample data",linewidth=1)
plt.show()

2）结果图

3）分析
从散点图可以看出，样本点基本是围绕箭头所示的直线分布的。所以先以直线模型对数据进行拟合

3.2 第二步：使用最小二乘法算法求拟合直线

1）代码及其说明

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重

##需要拟合的函数func :指定函数的形状 k= 0.42116973935 b= -8.28830260655
def func(p,x):
    k,b=p
    return k*x+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)


#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="sample data",linewidth=2)

#画拟合直线
x=np.linspace(105,142,100) ##在105-142直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="Fitting straight line",linewidth=2)
plt.legend() #绘制图例
plt.show()

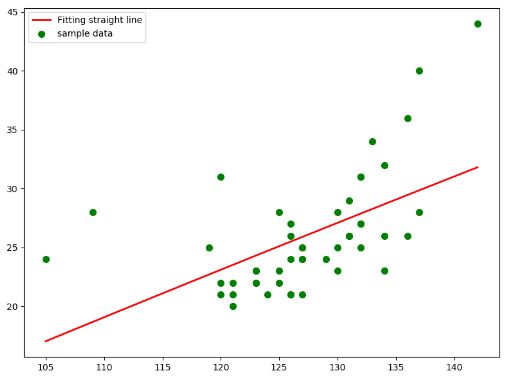
2）结果图

3）分析
从图上看，拟合效果还是不错的。样本点基本均匀的分布在回归线两边，没有出现数据点严重偏离回归线的情况。

3.3 第三步：验证回归线的拟合程度—残差分布图

1）代码及其说明

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重
xy_res=[]

##计算残差
def residual(x,y):
    res=y-(0.42116973935*x-8.28830260655)
    return res

##读取残差
for d in range(0,len(Xi)):
    res=residual(Xi[d],Yi[d])
    xy_res.append(res)
##print(xy_res)

##计算残差平方和:22.8833439288 -->越小拟合情况越好
xy_res_sum=np.dot(xy_res,xy_res)
#print(xy_res_sum)

##如果数据拟合模型效果好，残差应该遵从正态分布(0,d*d:这里d表示残差)
#画样本点
fig=plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
ax=fig.add_subplot(111)
fig=qqplot(np.array(xy_res),line='q',ax=ax)
plt.show()

2）结果图

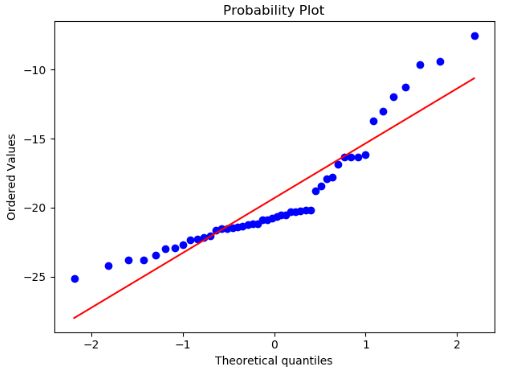
3）分析
上图为Q-Q图，原理：如果两个分布相似，则该Q-Q图趋近于落在y=x线上。如果两分布线性相关，则点在Q-Q图上趋近于落在一条直线上，但不一定在y=x线上。Q-Q图可以用来可在分布的位置-尺度范畴上可视化的评估参数。
从图上可以看出，回归效果比较理想，但不是最理想的

4）以下代码可以同样实现上述图示：

import numpy as np
import scipy.stats as stats
import pylab

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重
xy_res=[]

##计算残差
def residual(x,y):
    res=y-(0.42116973935*x-8.28830260655)
    return res

##读取残差
for d in range(0,len(Xi)):
    res=residual(Xi[d],Yi[d])
    xy_res.append(res)
##print(xy_res)

##计算残差平方和:22.8833439288 -->越小拟合情况越好
xy_res_sum=np.dot(xy_res,xy_res)
#print(xy_res_sum)

##如果数据拟合模型效果好，残差应该遵从正态分布(0,d*d:这里d表示残差)
#画样本点
stats.probplot(np.array(xy_res),dist="norm",plot=pylab)
pylab.show()

3.4 第四步：验证回归线的拟合程度—标准化残差

1）代码及其说明

import numpy as np
import matplotlib.pyplot as plt

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重
xy_res = []


##计算残差
def residual(x, y):
    res = y - (0.42116973935 * x - 8.28830260655)
    return res


##读取残差
for d in range(0, len(Xi)):
    res = residual(Xi[d], Yi[d])
    xy_res.append(res)
##print(xy_res)

##计算残差平方和:22.8833439288 -->越小拟合情况越好
xy_res_sum = np.dot(xy_res, xy_res)

'''
      标准残差:  （残差-残差平均值）/残差的标准差
'''

'''
      标准残差图：
    1.标准残差是以拟合模型的自变量为横坐标，以标准残差为纵坐标形成的平面坐标图像
    2.试验点的标准残差落在残差图的(-2,2)区间以外的概率<=0.05.若某一点落在区间外，可判为异常点
    3.有效标准残差点围绕y=0的直线上下完全随机分布，说明拟合情况良好
    4.如果拟合方程原本是非线性模型，但拟合时却采用了线性模型，标准化残差图就会表现出曲线形状，产生
      系统性偏差
'''

##计算残差平均值
xy_res_avg = 0
for d in range(0, len(xy_res)):
    xy_res_avg += xy_res[d]

xy_res_avg /= len(xy_res)

# 残差的标准差
xy_res_sd = np.sqrt(xy_res_sum / len(Xi))
##标准化残差
xy_res_sds = []

for d in range(0, len(Xi)):
    res = (xy_res[d] - xy_res_avg) / xy_res_sd
    xy_res_sds.append(res)

# print(xy_res_sds)

# 标准化残差分布
plt.figure(figsize=(8, 6))  ##指定图像比例： 8：6
plt.scatter(Xi, xy_res_sds)
plt.show()

'''
  1.绝大部分数据分布在(-2,+2)的水平带状区间内，因此模型拟合较充分
  2.数据点分布稍均匀，但没有达到随机均匀分布的状态。此外，部分数据点还呈现某种曲线波动形状，
    有少许系统性偏差。因此可能采用非线性拟合效果会更好
'''

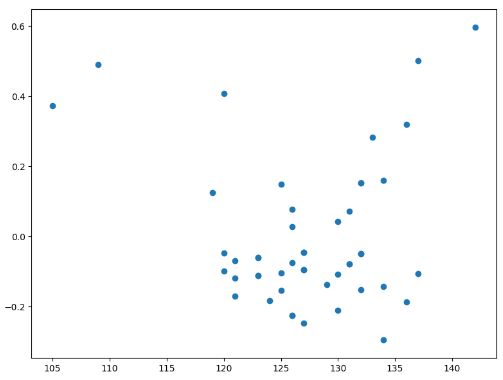
2）结果图

3）分析
数据点分布还是存在一定的变化趋势的。

3.5 第五步：使用曲线模型拟合数据

1）代码及其说明

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重

##需要拟合的函数func :指定函数的形状 k= 0.860357336936 b= -19.6659389666
def func(p,x):
    k,b=p
    return x**k+b

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
k,b=Para[0]
print("k=",k,"b=",b)


#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="sample data",linewidth=2)

#画拟合直线
x=np.linspace(105,142,100) ##在105-142直接画100个连续点
y=x**k+b ##函数式
plt.plot(x,y,color="red",label="Fitting straight line",linewidth=2)
plt.legend() #绘制图例
plt.show()

2）结果图

3）分析
由于标准化残差的分布图，部分数据的趋势与幂函数在第一象限的图像类似，所以采用了y=xa +b的函数形式，截距b是为了图像可以在Y轴上下移动

3.6 第六步：验证回归线的拟合程度—残差分布图

1）代码及其说明

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重
xy_res=[]

##计算残差
def residual(x,y):
    res=y-(x**0.860357336936-19.6659389666)
    return res

##读取残差
for d in range(0,len(Xi)):
    res=residual(Xi[d],Yi[d])
    xy_res.append(res)
##print(xy_res)

##计算残差平方和:22.8833439288 -->越小拟合情况越好
xy_res_sum=np.dot(xy_res,xy_res)
#print(xy_res_sum)

##如果数据拟合模型效果好，残差应该遵从正态分布(0,d*d:这里d表示残差)
#画样本点
fig=plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
ax=fig.add_subplot(111)
fig=qqplot(np.array(xy_res),line='q',ax=ax)
plt.show()

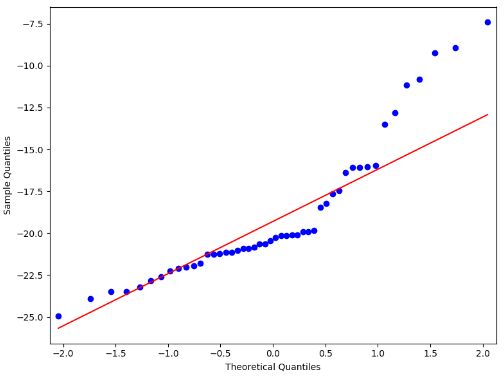
2）结果图

3）分析
从图上可以看出，回归效果也比较理想

3.7 第七步：验证回归线的拟合程度—标准化残差

1）代码及其说明

import numpy as np
import matplotlib.pyplot as plt

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([105,109,119,120,120,120,121,121,121,123,123,123,123,124,125,125,125,126,126,126,126,126,127,127,127,127,127,129,130,130,130,131,131,131,132,132,132,132,132,133,134,134,134,136,136,137,137,142]) #身高
Yi=np.array([24,28,25,31,22,21,21,22,20,23,22,23,22,21,28,23,22,21,26,24,21,27,25,25,24,24,21,24,25,23,28,29,26,26,31,27,27,31,25,34,23,26,32,36,26,40,28,44])#体重
xy_res = []


##计算残差
def residual(x, y):
    res = y - (x ** 0.860357336936 - 19.6659389666)
    return res


##读取残差
for d in range(0, len(Xi)):
    res = residual(Xi[d], Yi[d])
    xy_res.append(res)
##print(xy_res)
##计算残差平方和:22.881076636 -->越小拟合情况越好
xy_res_sum = np.dot(xy_res, xy_res)
# print(xy_res_sum)

'''
      标准残差:  （残差-残差平均值）/残差的标准差
'''
##计算残差平均值
xy_res_avg = 0
for d in range(0, len(xy_res)):
    xy_res_avg += xy_res[d]

xy_res_avg /= len(xy_res)

# 残差的标准差
xy_res_sd = np.sqrt(xy_res_sum / len(Xi))

##标准化残差
xy_res_sds = []

for d in range(0, len(Xi)):
    res = (xy_res[d] - xy_res_avg) / xy_res_sd
    xy_res_sds.append(res)

print(xy_res_sds)

# 标准化残差分布
plt.figure(figsize=(8, 6))  ##指定图像比例： 8：6
plt.scatter(Xi, xy_res_sds)
plt.show()

'''
  1.绝大部分数据分布在(-2,+2)的水平带状区间内，因此模型拟合较充分
  2.数据点分布稍均匀，但没有达到随机均匀分布的状态。此外，部分数据点还呈现某种曲线波动形状，
    有少许系统性偏差。因此可能采用非线性拟合效果会更好
'''

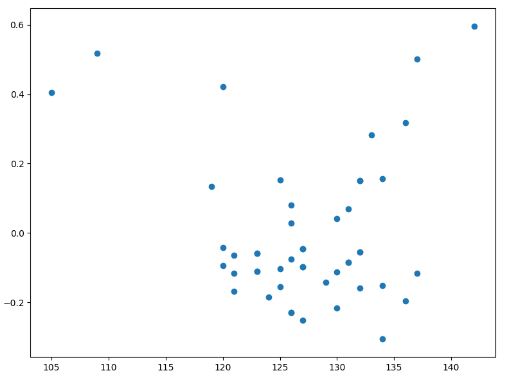
2）结果图

3）分析
数据点分布趋和直线回归方程基本一样

机器学习—线性回归之最小二乘法

1 什么是”最小二乘法”呢？

2 如何理解最小二乘法

3 实际应用的一个完整示例

3.1 第一步：准备样本数据并绘制散点图

3.2 第二步：使用最小二乘法算法求拟合直线

3.3 第三步：验证回归线的拟合程度—残差分布图

3.4 第四步：验证回归线的拟合程度—标准化残差

3.5 第五步：使用曲线模型拟合数据

3.6 第六步：验证回归线的拟合程度—残差分布图

3.7 第七步：验证回归线的拟合程度—标准化残差

你可能感兴趣的:(机器学习—线性回归之最小二乘法)

机器学习—线性回归之最小二乘法

1 什么是”最小二乘法”呢？

2 如何理解最小二乘法

3 实际应用的一个完整示例

3.1 第一步：准备样本数据并绘制散点图

3.2 第二步： 使用最小二乘法算法求拟合直线

3.3 第三步： 验证回归线的拟合程度—残差分布图

3.4 第四步： 验证回归线的拟合程度—标准化残差

3.5 第五步：使用曲线模型拟合数据

3.6 第六步：验证回归线的拟合程度—残差分布图

3.7 第七步：验证回归线的拟合程度—标准化残差

你可能感兴趣的:(机器学习—线性回归之最小二乘法)

3.2 第二步：使用最小二乘法算法求拟合直线

3.3 第三步：验证回归线的拟合程度—残差分布图

3.4 第四步：验证回归线的拟合程度—标准化残差